Pascal's Rule in NMR Spectroscopy ( n+1 )
Pascal's Rule in NMR spectroscopy, also known as the (N+1) rule, is an empirical rule used to predict the multiplicity and splitting pattern of peaks in 1H and 13C NMR spectra. It states that if a nucleus is coupled to N number of equivalent nuclei, the multiplicity of the peak is N+1. The rule help
1 views • 30 slides
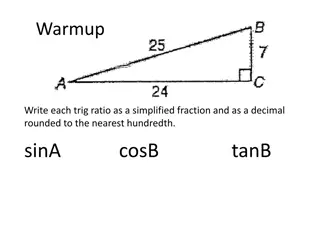
The World of Triangles
Dive into the realm of triangles, from basic properties like sides and angles to the classification into acute, obtuse, right, scalene, isosceles, equilateral, and equiangular triangles. Discover concepts like congruence, the Pythagorean theorem, and the significance of the hypotenuse in right trian
0 views • 26 slides
Trigonometry Applications and Challenge: Helicopter and Truck Problem
Explore trigonometry concepts, solve right triangles using trig ratios and the Pythagorean Theorem, find missing sides and angles, and apply trigonometry to real-life scenarios. Dive into trigonometry word problems, including angles of elevation and depression, and tackle a challenging problem invol
0 views • 8 slides
Trigonometric Integrals: Strategies and Identities
Learn useful trigonometric identities and strategies for integrating powers of sine and cosine. Understand when to use Pythagorean, Half or Double Angle Identities, and how to handle odd or even powers efficiently. Examples provided for clarity.
1 views • 14 slides
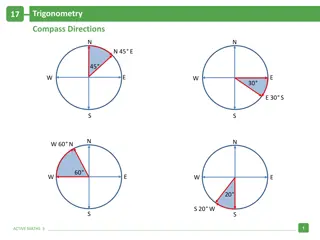
Trigonometry and Compass Directions Problem Solving
In this trigonometry problem, a ship travels from point A to point B and then to point C in specific directions. By applying the Pythagorean theorem, the distance from point C to A is calculated to be 7.2 km. The angle BCA is determined to be 34 degrees, and the direction of point C from A is found
0 views • 5 slides
Exploring Square Numbers and Pythagorean Triplets
Introduction to square numbers, their properties, patterns, and Pythagorean triplets. Learn about non-perfect square numbers, rules for determining Pythagorean triplets, and solving related problems through examples and worksheets.
0 views • 13 slides
Understanding the Pythagorean Theorem and Right-Angled Triangles
Explore the Pythagorean Theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b). Learn how to identify the hypotenuse, use the theorem to find missing lengths, and visually understand th
0 views • 25 slides
Mathematicians Through Time: Pioneers in Mathematics
Delve into the lives and contributions of influential mathematicians throughout history, from Pythagoras and Euclid to Archimedes, Fibonacci, Descartes, and Isaac Newton. Learn about their groundbreaking discoveries, from the Pythagorean theorem to the Fibonacci sequence and the Cartesian plane, sha
8 views • 10 slides
Midpoint and Distance in Coordinate Plane
This content covers the concepts of finding midpoints and distances in the coordinate plane. It explains how to calculate the midpoint of line segments on a number line and in a coordinate plane using the midpoint formula. Additionally, it discusses finding the distance between two points using the
0 views • 7 slides
Exploring the Pythagorean Theorem and Its Origins
The Pythagorean Theorem, named after the ancient Greek mathematician Pythagoras, is a fundamental principle in geometry relating to right triangles. While Pythagoras is credited with offering a proof of the theorem, evidence suggests that earlier civilizations like the Babylonians and ancient Chines
0 views • 21 slides
Understanding the Pythagorean Theorem: History, Application, and Baseball Problem
Pythagoras, a renowned mathematician from ancient times, formulated the Pythagorean Theorem to calculate the lengths of sides in right triangles. This theorem has significant implications in various fields, aiding in distance computation, navigation, and ramp design. Moreover, its practical applicat
0 views • 14 slides
Pythagoras: The First True Mathematician from Greece
Pythagoras, born in 560-480 BC in Greece, is often regarded as the first true mathematician. He founded the Pythagoreans, who believed in the concept that "All is Number," emphasizing the importance of numbers in the universe. Pythagoras is renowned for the Pythagorean theorem and his work in geomet
0 views • 12 slides
Exploring Squares and Square Roots: Concepts and Applications
Delve into the world of squares and square roots in this comprehensive module for Class VIII. Discover how to find the squares of numbers efficiently, explore Pythagorean triplets, and understand their general forms. Uncover the beauty of mathematical relationships and patterns in this engaging lear
1 views • 10 slides
Exploring Mathematics: Squares, Square Roots, and Area Formulas
Discover the fascinating world of mathematics by delving into squares, square roots, and area formulas. Explore the concepts of squares, rectangles, and triangles while uncovering the relationships between them. Learn about exponents, the Pythagorean Theorem, and the significance of square roots. En
0 views • 11 slides
Zero-Shot Relation Extraction Based on Contrast Learning
This paper presents a zero-shot relation extraction approach based on contrast learning, aiming to improve the efficiency of relation extraction tasks. The methodology involves utilizing a knowledge graph to extract relational triplets and leveraging zero-shot learning to automate the process. The s
0 views • 21 slides
Introduction to Applying Pythagorean Theorem in Right Triangles
In this lesson, we will learn how to apply the Pythagorean Theorem to find missing side lengths of right triangles. The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Through examples and practice problems,
0 views • 13 slides
Understanding Trigonometric Identities for Double Angles
Special identities like the Pythagorean identity and double angle identities for sine and cosine are explored in this content. The Pythagorean identity states that cosine squared plus sine squared equals one, while the double angle identities provide formulas for cosine of double angles. Through the
0 views • 13 slides
Understanding Euclidean Geometry and the Pythagorean Theorem
Explore the foundations of Euclidean Geometry, delve into the Pythagorean Theorem, discover the postulates of Euclid, and learn about distance functions, Euclidean distance, taxi-cab metric, circles, and isometries and congruence. Unravel the rich history, key principles, and practical applications
0 views • 37 slides
Exploring Text Mining Methods and Applications
Text mining is a complex field that presents a significant disjunction in methods compared to other data analysis approaches. Pre-LLM methods are still relevant in various applications, showcasing different performance in text mining tasks. The analysis involves examining individual words' presence,
0 views • 13 slides
Implicit Citations for Sentiment Detection: Methods and Results
This study focuses on detecting implicit citations for sentiment detection through various tasks such as finding zones of influence, citation classification, and corpus construction. The research delves into features for classification, highlighting the use of n-grams, dependency triplets, and other
0 views • 14 slides
Mastering C++ Functions and Modularity with Example Programs
Learn how to effectively use functions in C++, including how to declare variables, control flow using if-else statements and loops, and create blocks of statements. Dive into the concept of functions, pre-defined functions, and practical applications like the Pythagorean Theorem calculation in C++.
0 views • 67 slides
Exploring Commensurable Triangles: Sides vs. Angles
Delve into the world of commensurable triangles through the lens of sides and angles. Discover the relationships between integer triples, Pythagorean triangles, Heronian triangles, and the fascinating properties that arise from their configurations. Uncover the intriguing patterns and dense sets wit
1 views • 23 slides
Trigonometry Review and Essential Concepts Explained
Refresh your knowledge of trigonometry with a thorough review of key concepts such as SOH-CAH-TOA, trigonometric identities, Pythagorean theorem, and more. Understand the significance of standard position, terminal side of angles, unit circle intersections, quadrant signs, and the law of cosines. Ex
0 views • 8 slides
Exploring Pythagorean Theorem and Converse in Geometry
Uncover the mysteries of the Pythagorean Theorem and its converse in this educational content. Discover how to apply the theorem to find hypotenuses, determine Pythagorean triples, and verify right triangles. Engage in solving geometric problems involving triangles, lengths, and distances with pract
0 views • 11 slides
4 Seat Stroller – The Ultimate Solution for Growing Families!
Take the hassle out of managing multiple children with a convenient 4 seat stroller. Designed for ease of use, this stroller is perfect for families with twins, triplets, or a mix of toddlers and newborns. Its sturdy build and smooth steering offer c
2 views • 6 slides
Understanding Vectors: Concepts, Operations, and Applications
Vectors are quantities defined by magnitude and direction, essential in various fields like physics and mathematics. Learn about vector properties, examples, operations like addition and multiplication, as well as applications such as understanding displacement, velocity, and acceleration. Dive into
0 views • 20 slides