Learn about the Portfolio Matrix, a strategic tool assessing products based on industry growth and market share. Explore the BCG matrix, its four categories, and how it guides decision-making for products' future success.

1 views • 14 slides

Composite materials consist of reinforcement and matrix components, each serving a specific purpose to enhance the properties of the composite. The reinforcement phase provides strength and stiffness, while the matrix transfers loads and protects the fibers. Different types of reinforcements and mat

8 views • 18 slides

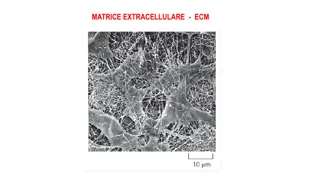
Extracellular Matrix (ECM) is a complex network of proteins, glycoproteins, and macromolecules that provide structural support, regulate cell activities, and play crucial roles in various tissues. It consists of two main types - interstitial matrix and basement membrane, each serving specific functi

12 views • 25 slides

Completing a Trainer Matrix is essential for Registered Training Organizations (RTOs) to demonstrate compliance with Standards for RTOs 2015, specifically Clauses 1.13 to 1.16. This matrix outlines requirements for trainers, including holding relevant qualifications, industry skills, and maintaining

2 views • 38 slides

Explore the concept of matrix organizations, challenges faced in managing multiple principals, and the importance of accountability, prioritization, and coordination. Learn how matrix structures evolved, their prevalence in modern workforce, and the impact on industries like architecture firms.

1 views • 22 slides

Use the Eisenhower Matrix template to effectively prioritize project tasks by distinguishing between urgent and important activities. Delegate, delete, or tackle tasks based on their significance for optimal time management. An example matrix provided showcases various tasks categorized as urgent/im

1 views • 4 slides

Proposal and implementation plan for interlock actions and matrix coordination between DSS server rack and user areas in SR1. Includes agreements, alarms-actions matrix finalization, cable routing, server installation, and commissioning with dummy loads. Discusses CO2 plant signals, temperature moni

4 views • 7 slides

Delve into the world of matrices in Precalculus with a focus on identifying matrix orders, creating augmented matrices for systems of equations, transforming matrices into row-echelon form, and solving linear equations using matrices. Explore elementary row operations, row-echelon form, and reduced

1 views • 37 slides

Singular Value Decomposition (SVD) is a powerful method for solving systems of linear equations or matrices that are singular or close to singular. When LU-decomposition or Gaussian elimination fail, SVD provides a stable matrix decomposition helpful in various applications. It is particularly usefu

0 views • 17 slides

A Governance Decision Authorities Matrix is a crucial tool that articulates roles and responsibilities for major decision-making within a system. This template provides a starting point for customizing governance structures, focusing on areas like fiduciary responsibilities, strategic planning, qual

1 views • 9 slides

The Singular Value Decomposition (SVD) is a powerful factorization method for matrices, extending the concept of eigenvectors and eigenvalues to non-symmetric matrices. This decomposition allows any matrix to be expressed as the product of three matrices: two orthogonal matrices and a diagonal matri

0 views • 35 slides

Singular Value Decomposition (SVD) is a powerful method that decomposes a matrix into orthogonal matrices and diagonal matrices. It helps in understanding the range, rank, nullity, and goal of matrix transformations. The method involves decomposing a matrix into basis vectors that span its range, id

0 views • 21 slides

Singular Value Decomposition (SVD) is a powerful technique in linear algebra that breaks down any matrix into orthogonal stretching followed by rotation. It reveals insights into transformations, basis vectors, eigenvalues, and eigenvectors, aiding in understanding linear transformations in a geomet

3 views • 18 slides

Diagonalization plays a crucial role in converting complex problems into simpler ones by allowing matrices to be represented in a diagonal form. The process involves finding eigenvalues and corresponding eigenvectors, ultimately leading to a diagonal matrix representation. However, careful considera

0 views • 36 slides

Discover the concept of diagonalization in linear algebra through eigenvectors, eigenvalues, and diagonal matrices. Learn the conditions for a matrix to be diagonalizable, the importance of eigenvectors in forming an invertible matrix, and the step-by-step process to diagonalize a matrix by finding

0 views • 26 slides

Discover the innovative methods and applications of open quantum systems techniques for density matrix minimization. Explore the motivation behind the research, early developments, purification processes, linear scaling potentials, Bloch's method intricacies, quantum channel algorithms, canonical de

0 views • 22 slides

Explore the application of matrix algebra in solving systems of equations through a practical example involving the interpolation of rocket velocity data. Learn how to set up equations in matrix form to find the coefficients profile of the velocity polynomial, illustrating the concept effectively.

0 views • 71 slides

The rank of a matrix is the maximum number of linearly independent columns, while the nullity is obtained by subtracting the rank from the number of columns. Linearly independent columns form the basis for the rank of a matrix, helping determine if a given matrix has a unique solution, infinite solu

0 views • 6 slides

Explore the concept of matrix factorization for recovering latent factors in a matrix, specifically focusing on user ratings of movies. This technique involves decomposing a matrix into multiple matrices to extract hidden patterns and relationships. The process is crucial for tasks like image denois

0 views • 50 slides

Explore the eigenvalues of sums of non-commuting random symmetric matrices in the context of quantum information. Delve into the complexities of eigenvalue distributions in various scenarios, including random diagonals, orthogonal matrices, and symmetric matrix sums. Gain insights into classical and

0 views • 24 slides

In this research, the complexity of rectangular matrix multiplication is enhanced by analyzing the fourth power of the Coppersmith-Winograd tensor. By extending the understanding of the tensor's power, significant advancements have been made in the efficiency of non-square matrix multiplication, sur

0 views • 25 slides

Explore the concepts of linear equations, matrix forms, determinants, and finding solutions for variables like x1, x2, x3. Learn about Cramer's Rules, Adjoint Matrix, and calculating the inverse of a matrix through examples and formulas.

0 views • 24 slides

Factor analysis involves rotation of the factor loading matrix to enhance interpretability. This process was originally done manually but is now performed analytically with computers. Factors can be orthogonal or oblique, impacting the interpretation of factor loadings. Understanding rotation simpli

0 views • 42 slides

Priority Matrix is a valuable tool in the A/C/E industry, allowing teams to prioritize tasks efficiently, communicate priorities effectively, and track progress accurately. Real teams benefit from its use cases in prioritization, communication, and progress tracking, creating a roadmap for workflow

0 views • 23 slides

Explore the Student Discipline Reporting and Unsafe School Choice Option program in Georgia schools, led by Jeff Hodges and Richard Woods. Learn about the Discipline Matrix, its purpose, and how it improves data accuracy, transparency, and addresses concerns related to discipline actions. Discover h

0 views • 35 slides

The Global Matrix 4.0 Spanish Report Card Leaders Meeting provides insights into national and regional report cards, introduction of Spanish leaders, and discussions on national coordination and future opportunities for various regions. The meeting aims to harmonize messaging, share information, and

0 views • 9 slides

Explore the concepts of simultaneous linear equations, homogeneous and non-homogeneous systems, orthogonal matrices, and various types of quadratic forms in linear algebra. Learn about the characteristics of positive definite, semi-positive definite, and negative definite quadratic forms represented

0 views • 7 slides

Investigate how matrix physics can provide a novel approach in understanding global climate models, focusing on realistic global flows and anomalies. The study aims to move beyond traditional algorithmic rule sets, examining how deviations from time mean flows can affect climate and weather patterns

0 views • 35 slides

Explore the innovative approach of circuit simulation via matrix exponential operators as proposed by CK Cheng from UC San Diego. The method involves utilizing general matrix exponentials, Krylov spaces, Arnoldi orthonormalization, and inverting Krylov subspaces for accurate simulations. These techn

0 views • 28 slides

Advanced techniques for orthogonal skyline counting queries discuss optimal planar solutions, dividing and conquering for topmost point identification, efficient vertical slab counting, succinct data structures for prefix sums and range maxima, upper bounds on degree and multi-slab queries, as well

0 views • 11 slides

Conducting a multiple regression analysis on the energy consumption of luxury hotels in Hainan Province, China using matrix form in Excel. The dataset includes 19 luxury hotels with the dependent variable being energy consumption (1M kWh) and predictors such as area, age, and effective number of gue

0 views • 13 slides

Simplify hotel operations and enhance guest experiences with Matrix Hospitality Solution. From enhancing staff efficiency to boosting revenue generation opportunities, Matrix offers a comprehensive suite of features to meet the diverse needs of hotels. Its modular configuration, scalable platform, a

0 views • 36 slides

The pilot run matrix measurements were conducted following the 7th Belle II VXD workshop and the 18th International Workshop on DEPFET Detectors and Applications by Rainer H. Richter and Paola Avella for the MPP/HLL team. The measurements included assessing defects, diode integrity, metal shorts, an

0 views • 30 slides

Composite materials are made of reinforcing fibers and matrix materials, with the matrix serving to protect and enhance the properties of the composite. There are three main types of composite matrix materials: metal matrix composites (MMC), ceramic matrix composites (CMC), and polymer matrix compos

0 views • 22 slides

The document discusses the need for short simultaneous feedback from multiple STAs in IEEE 802.11 systems for improved efficiency. It introduces the NDP feedback mechanism and proposes a signaling technique to efficiently collect feedback from a high number of STAs. The mechanism involves UL MU tran

0 views • 19 slides

A detailed exploration of functions of matrices, including exponential of a matrix, eigenvector sets, eigenvalues, Jordan-Canonical form, and applications of Taylor series to compute matrix functions like cosine. The content provides a deep dive into spectral mapping, eigenvalues, eigenvectors, and

0 views • 53 slides

Matrix multiplication is a fundamental operation with diverse applications across scientific research. Parallel computation for matrix multiplication involves distributing the computational workload over multiple processors, improving efficiency. Different algorithms have been developed for multiply

0 views • 36 slides

Explore the Polynomial Method in classical algorithms, focusing on Orthogonal Vectors, All-Pair-Shortest-Path, and Approximate Closest Pair. Learn how the Polynomial Method works through batch evaluation for multi-variable polynomials and fast matrix multiplication. Discover insights on low-rank dec

0 views • 13 slides

Exploring the computational complexity of low-polynomial-time problems, this workshop delves into the Orthogonal Vectors Problem and its conjectures. It introduces concepts like the Sparse OV Problem, first-order graph properties, and model checking in graphs. Discussing the hardness of problems rel

2 views • 22 slides

Non-Orthogonal Multiple Access (NOMA) technology has revolutionized the way multiple users' messages are superimposed and transmitted over the same frequency simultaneously. NOMA offers enhanced spectral efficiency, massive connectivity, and increased throughput compared to traditional multiple acce

0 views • 5 slides