Understanding Bernoulli's Equation in Fluid Mechanics
Bernoulli's equation, a fundamental principle in fluid dynamics, relates pressure, kinetic energy, and potential energy of a fluid flowing in a pipe. Through examples and explanations, explore how this equation can be used to calculate velocity, pressure differences, and forces in various scenarios
1 views • 12 slides
Thermodynamics of Solar Plasma: SAHA-S Equation of State and Recent Results
SAHA-S equation of state (EOS) presents the current state and recent results in thermodynamics of solar plasma. Key authors V.K. Gryaznov, A.N. Starostin, and others have contributed to this field over 20 years. The equilibrium composition between 145 species, including elements and all ions, is exp
1 views • 23 slides
If you are looking for Gasfitting in Hutt Central
If you are looking for Gasfitting in Hutt Central, Welcome to Sinclair Plumbing in Stokes Valley. We fix leaking hot water cylinders, dripping taps, or burst pipes. Call us today. We provide plumbing maintenance and repair services to the residents of Hutt Valley\/Wellington regions. We offer a wide
0 views • 6 slides
Overview of Fluid Mechanics: Branches, Flow Types, and Equations
Fluid mechanics is subdivided into three branches: Fluid Static, Kinematics, and Hydrodynamics. The study of fluid flow includes different types such as uniform, non-uniform, steady, and unsteady flow. The motion of fluid particles obeys Newton's laws, and the conservation of mass and energy plays a
1 views • 4 slides
Understanding the Quantity Theory of Money: Fisher vs. Cambridge Perspectives
The Quantity Theory of Money explains the relationship between money supply and the general price level in an economy. Fisher's Equation of Exchange and the Cambridge Equation offer different perspectives on this theory, focusing on money supply vs. demand for money, different definitions of money,
0 views • 7 slides
Understanding Structural Equation Modeling (SEM) and Quality of Life Analysis
Structural Equation Modeling (SEM) is a statistical technique used to analyze relationships between variables, including quality of life factors such as physical health and mental well-being. Quality of life is a multidimensional concept encompassing various aspects like social relationships, living
0 views • 21 slides
Understanding Freezing Time and Freezers for Food Products
Importance of freezing time in the design of freezers is crucial for maintaining food quality during storage. Plank's equation is used to calculate freezing time based on various parameters. Limitations and assumptions of the equation need to be considered for accurate results.
0 views • 15 slides
Understanding Waveguiding Systems and Helmholtz Equation in Microwave Engineering
Waveguiding systems are essential in confining and channeling electromagnetic energy, with examples including rectangular and circular waveguides. The general notation for waveguiding systems involves wave propagation and transverse components. The Helmholtz Equation is a key concept in analyzing el
2 views • 50 slides
Understanding Thermodynamics and Fluid Mechanics Fundamentals for Efficiency
Explore key concepts in thermodynamics and fluid mechanics such as the equation of continuity, the first law of thermodynamics, the momentum equation, Euler's equation, and more. Learn about efficiency, internal energy, and the laws governing energy transfer in various systems. Delve into topics lik
2 views • 12 slides
Understanding Fluorescence Microscopy: Principles and Applications
Fluorescence microscopy, pioneered by British scientist Sir George G. Stokes, reveals hidden details in specimens using fluorescent dyes that emit light of longer wavelengths. This innovative technique allows for visualization of cellular components that are otherwise colorless under conventional mi
0 views • 19 slides
Understanding the Hammett Equation in Chemical Reactions
The Hammett equation explores how substituents influence the dissociation of benzoic acid, affecting its acidity. By quantifying this influence through a linear free energy relationship, the equation helps predict the impact of substituents on different processes. Through parameter definitions and m
0 views • 9 slides
Introduction to Dynamic Structural Equation Modeling for Intensive Longitudinal Data
Dynamic Structural Equation Modeling (DSEM) is a powerful analytical tool used to analyze intensive longitudinal data, combining multilevel modeling, time series modeling, structural equation modeling, and time-varying effects modeling. By modeling correlations and changes over time at both individu
0 views • 22 slides
Understanding Particle Motion in Fluids: Dynamics and Phenomena
Exploring the intricate dynamics of particle motion within fluids, this content delves into mechanical micro-processes, particle velocity, terminal velocity, flow regimes, and the calculation of drag coefficients. It covers the Stokes region, laminar flow conditions, and considerations for transient
0 views • 28 slides
Understanding Separation Columns in Chemical Engineering
Explore the world of separation columns including distillation, absorption, and extraction, along with empirical correlations, minimum number of stages, Fenske equation, Underwood equation, Kirkbride equation, examples, and solutions presented by Dr. Kh. Nasrifar from the Department of Chemical and
5 views • 15 slides
Comprehensive Overview of Freezing Time Methods in Dairy Engineering
Neumann, Tao, and Non-Dimensional methods are key approaches for determining freezing times in unsteady state heat transfer processes in dairy engineering. The Neumann Problem, Tao Solutions, and Cleland and Earle Non-Dimensional Equation offer distinct equations and models to calculate freezing tim
1 views • 8 slides
Introduction to Quantum Mechanics: Energy Levels and Schrödinger Equation
Quantum mechanics reveals that all systems possess discrete energy levels, determined by solving the Schrödinger equation where the Hamiltonian operator represents total energy. In a particle-in-a-box scenario, potential energy is infinite outside the box. The Schrödinger equation simplifies to a
0 views • 12 slides
Fundamental Comparison: Wheeler-DeWitt vs. Schrödinger Equation
The debate on whether the Wheeler-DeWitt equation is more fundamental than the Schrödinger equation in quantum gravity remains inconclusive. While the Wheeler-DeWitt equation presents an elegant formulation, the Schrödinger equation is essential in specific cases. The issue of time and coordinate
0 views • 6 slides
Cash Flow Planning in Bellevue | Contact Now for Advice | Avier Wealth Advisors
\nAvier Wealth Advisors provides expert cash flow planning in Bellevue, helping you manage income, expenses, and savings to achieve financial stability and long-term goals.
0 views • 1 slides
Understanding Open Channel Flow and Mannings Equation
This review covers hydraulic devices such as orifices, weirs, sluice gates, siphons, and outlets for detention structures. It focuses on open channel flow, including uniform flow and varied flow, and explains how to use Mannings equation for calculations related to water depth, flow area, and veloci
1 views • 43 slides
Exploring Membrane Potential Densities and the Fokker-Planck Equation in Neural Networks
Delve into the concepts of membrane potential densities and the Fokker-Planck Equation in neural networks, covering topics such as integrate-and-fire with stochastic spike arrival, continuity equation for membrane potential density, jump and drift flux, and the intriguing Fokker-Planck Equation.
0 views • 29 slides
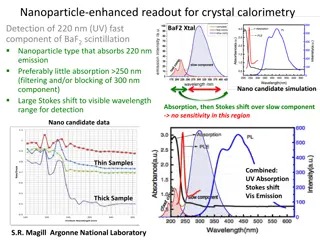
Nanoparticle-Enhanced Readout for Crystal Calorimetry: BaF2 Scintillation Detection
Nanoparticles with specific absorption and emission properties are explored to enhance the readout process for BaF2 crystal calorimetry, focusing on detecting the fast 220nm UV component. The goal is to achieve a large Stokes shift to the visible wavelength range for efficient detection, while minim
0 views • 7 slides
Leapfrog Scheme for Advection Equation
The provided images illustrate the Leapfrog scheme applied to an advection equation, focusing on the center method in time and space. The stability of the method is analyzed with assumptions regarding the behavior of the solution. Through the exploration of Courant numbers and CFL conditions, the st
0 views • 25 slides
Unveiling Untold Stories of Black American Involvement in Armed Conflicts
Discover the overlooked narratives of African Americans in historic armed conflicts, from the War of 1812 to Civil War battlefields. Explore individual accounts such as Ann Stokes, challenging conventional perceptions and benefiting from preservation programs like the American Battlefield Protection
0 views • 22 slides
Wealth Advisors in Bellevue WA | Avier Wealth Advisors
\nAvier Wealth Advisors offers personalized financial solutions from top wealth advisors in Bellevue, WA, helping you achieve long-term financial goals with expert guidance.
0 views • 2 slides
Wealth Advisors in Bellevue WA | Avier wealth advisors
\nAvier Wealth Advisors offers personalized financial solutions from top wealth advisors in Bellevue, WA, helping you achieve long-term financial goals with expert guidance.
0 views • 2 slides
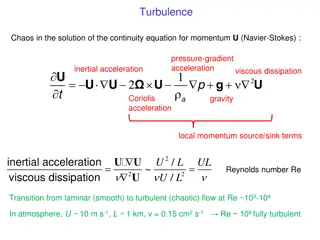
Understanding Turbulence in Fluid Dynamics: A Comprehensive Exploration
Exploring the complexities of turbulence in fluid dynamics, from the Navier-Stokes equations to subgrid transport and turbulent diffusion. Insights into the transition from laminar to turbulent flow, subgrid scale importance, and treatment of small-scale eddies are discussed. The impact of turbulenc
0 views • 9 slides
Wealth Advisors in Bellevue WA | Avier wealth advisors
\nAvier Wealth Advisors offers personalized financial solutions from top wealth advisors in Bellevue, WA, helping you achieve long-term financial goals with expert guidance.
0 views • 2 slides
Excel Tutorial: Finding Trendline Equation and Calculating Rates of Change
Learn how to find the equation of a trendline in Excel and use it to calculate rates of change. This step-by-step guide includes importing data, adding a trendline, displaying the equation, and interpreting it for analysis. Make the most of Excel's features for data analysis.
0 views • 11 slides
Linearized Boltzmann Equation in Statistical Mechanics
This lecture delves into the linearized Boltzmann equation and its applications in studying transport coefficients. The content covers the systematic approximation of transport coefficients, impact parameters of collisions, and the detailed solution for a dilute gas system. It explores the notation
0 views • 25 slides
Quantum Chemistry Learning Goals and Concepts
This content covers the learning goals and concepts of quantum chemistry leading up to the Schrodinger equation and potential energy wells, excluding the material on the hydrogen atom introduced later. It explores models of the atom, including observations of atomic spectra, the Bohr model, de Brogl
0 views • 22 slides
Analytical Solutions for 2D Heat Equation with Separation of Variables
Consider the steady-state 2D heat equation with constant thermal conductivity. Analyze analytical solutions using separation of variables method for a square plate with defined boundary conditions. Learn how to express the general form of solutions and apply them to the heat equation in Cartesian ge
0 views • 15 slides
Understanding Conservation of a Quantity in Fluid Motion
Today's lecture in Computational Earth Science delved into the Navier-Stokes Equation and the conservation of momentum in moving fluids. The discussion focused on the tricks involved in solving for pressure, dealing with repeating boundaries, and tracking eddies in channel flow. Through detailed ill
0 views • 44 slides
Dynamic Function for Basal Area of Trees Derived from Differential Equation
Mathematical methods presented by Braun and Simmons are used to derive a dynamic function for the basal area of individual trees from a production-theoretically motivated autonomous differential equation. The differential equation and general dynamic function are described, highlighting the relation
0 views • 45 slides
Understanding Vector Calculus II Concepts with Examples by Prof. Somesh Kr. Malhotra
Explore advanced topics in vector calculus including gradient, divergence, curl, and theorems like the Divergence Theorem and Stokes' Theorem. Follow along with examples presented in Cartesian, spherical, and cylindrical coordinates to deepen your understanding of vector calculus concepts.
0 views • 29 slides
Effects of Non-Spherical Ice Crystal Shape on Modeled Properties of Thin Tropical Tropopause Layer Cirrus
This study explores the impact of non-spherical ice crystal shapes on the properties of cirrus clouds in the thin tropical tropopause layer. Incorporating realistic ice crystal shapes into models affects fall speed, growth rate, and radiative absorption, influencing the time evolution of clouds. The
0 views • 38 slides
Analysis and Comparison of Wave Equation Prediction for Propagating Waves
Initial analysis and comparison of the wave equation and asymptotic prediction of a receiver experiment at depth for one-way propagating waves. The study examines the amplitude and information derived from a wave equation migration algorithm and its asymptotic form. The focus is on the prediction of
0 views • 23 slides
Two-Dimensional Mathematical Model of Flows in Thin Film Composite Membranes
This study presents a mathematical model for flows in thin film composite membranes, focusing on the permeation of solvent flux and solute rejection. Assumptions include incompressible fluid, constant diffusion of chemical species, and isothermal conditions. Equations describe water flux, solute flu
0 views • 19 slides
Understanding the Photoelectric Effect and Einstein's Equation
The photoelectric effect is explained by Einstein through assumptions of photons and their interaction with electrons on a metal surface. The maximum kinetic energy of ejected electrons depends on the frequency of incident radiation, as shown in Einstein's Equation. The greater the frequency, the hi
0 views • 6 slides
Graphical Solution of Equations Using GDC - Step-by-Step Guide
Learn how to solve equations graphically using a Graphic Display Calculator (GDC) with step-by-step instructions. Turn on the GDC, input the equation on Y1 and Y2, draw the graphs, and find the intersection point to determine the x-value. An example equation, 2x + 8 = x + 1, is solved using this met
0 views • 20 slides
Indiana's New Student-Centered Accountability System Overview
Explore Indiana's innovative student-centered accountability system introduced in February 2016 by Dr. Yvonne Stokes. The system focuses on growth performance, multiple measures, and how A-F school grades are calculated to assess English/Language Arts and Mathematics proficiency from grade levels 3
0 views • 12 slides