Exploring FAEST: Post-Quantum Signatures and Zero-Knowledge Proofs
Delve into the world of FAEST, a post-quantum signature scheme, with a focus on publicly verifiable zero-knowledge proofs. The presentation covers VOLE-in-the-Head, families of ZK proofs, and the application of VOLE in creating VOLE-ZK proofs. Learn about the background of VOLE, its use in the desig
1 views • 26 slides
Mathematical Definitions and Theorems Illustrated
In this collection of images, various mathematical concepts are visually presented, including definitions, theorems, and proofs. The slides cover a range of topics in a structured manner, providing a concise overview of key mathematical principles. From foundational definitions to detailed proofs, t
0 views • 12 slides
Understanding Sequences and Series in Mathematics
Sequences and series are fundamental concepts in mathematics, with sequences consisting of terms denoted as a1, a2, a3, ... and series involving the sum of terms in arithmetic and geometric progressions. Learn about arithmetic progression, geometric progression, terms, and formulas for finding sums
1 views • 11 slides
Geometric Series: Power Series Representations & Convergence
Geometric series analysis discusses the summation, convergence, and divergent properties within and outside the unit circle. The series' representation, convergence conditions, and extensions are explored through power series expansions and geometric series summations, providing a comprehensive unde
0 views • 50 slides
Understanding Indirect Proofs: Contradiction and Contraposition Examples
Indirect proofs offer a roundabout approach to proving statements, with argument by contradiction and argument by contraposition being the main techniques. Argument by contradiction involves supposing the statement is false and deriving a contradiction, while argument by contraposition relies on the
1 views • 18 slides
Understanding Stereochemistry: Isomers and Their Properties
Stereochemistry explores the fascinating world of isomers, including stereoisomers, geometric isomers, and structural isomers. Stereoisomers have the same molecular formula but differ in spatial arrangement, while geometric isomers lack free rotation around bonds. Structural isomers like dimethyl et
0 views • 27 slides
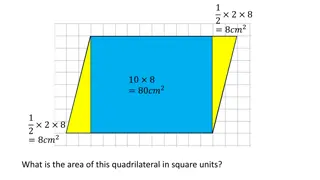
Geometric Problems and Solutions
Explore various geometric problems related to quadrilaterals, rectangles, parallelograms, and tangrams. Learn about finding areas, transforming shapes, and solving puzzles. Discover the principles behind turning a rectangle into a parallelogram and identifying areas of different geometric figures.
0 views • 7 slides
Understanding Algebraic Proofs and Equations
Explore algebraic proofs, equations solving techniques, and properties of equality through examples. Learn about the distributive property, temperature conversion, and problem-solving applications in algebra. Enhance your understanding of logic and algebraic reasoning.
0 views • 30 slides
Solving Bearings and Geometric Problems
This content discusses solving problems involving bearings, geometric shapes, and properties of triangles and lines. It covers determining bearings between points, finding angles in isosceles triangles, and understanding parallel lines and angles. The content also includes information on angles in q
0 views • 6 slides
Understanding Geometric Line Sweep Algorithms
Geometric Line Sweep is a powerful technique where an imaginary line sweeps over points, performing geometric operations at each point. This method can find minimum distances between points, overlapping rectangles, and more. By sorting points and efficiently processing them, it can enhance performan
0 views • 10 slides
Understanding Direct Proofs in Discrete Mathematics
Explore the principles of direct proof in discrete mathematics through a Peer Instruction approach by Dr. Cynthia Bailey Lee and Dr. Shachar Lovett. Learn how to prove theorems of the form "if p, then q" using logical rules, algebra, and math laws. Utilize a clear template for direct proofs, practic
0 views • 17 slides
Guide to Direct Proofs in Discrete Math
Dive into the world of direct proofs in discrete math with this comprehensive guide. Learn how to prove implications, create truth tables, and follow a step-by-step direct proof template. Test your understanding with engaging quizzes and practical examples. Master the art of logical reasoning and fo
0 views • 18 slides
Evolution of Proofs in Cryptography
Cryptography has evolved from classical proofs to interactive and probabilistically checkable proofs, enabling the development of applications like Non-Malleable and Chosen-Ciphertext Secure Encryption Schemes. Non-Malleability protects against active attacks like malleability and chosen-ciphertext
0 views • 29 slides
Post-Quantum Cryptography Security Proofs and Models Overview
Explore the various aspects of post-quantum cryptography security, including evaluation criteria, building public key cryptography (PKC) systems, security proofs, digital signatures, and reduction problems. Dive into topics such as performance, cryptanalysis, provable security, standard models, exis
0 views • 42 slides
Geometric Routing Concepts and Byzantine Fault Tolerance
Geometric Routing enables routing without overhead, where each node knows its global coordinates and forwards messages based on proximity to the destination. Byzantine Faults pose challenges with arbitrary node behavior, but a Byzantine-Robust Geometric Routing algorithm addresses this in a 3-connec
2 views • 33 slides
Mathematical Proof Techniques and Examples
Explore various proof techniques in mathematics including direct proofs, proofs by cases, proofs by contrapositive, and examples showing how to prove statements using algebra, definitions, and known results. Dive into proofs involving integers, even and odd numbers, and more to enhance your understa
2 views • 13 slides
Practical Statistically-Sound Proofs of Exponentiation in Any Group
The paper presents practical and statistically sound proofs of exponentiation in any group. It discusses the computation process, applications in verifiable delay functions and time-efficient arguments for NP, as well as interactive protocols and the overview of PoEs. The research contributes a stat
0 views • 18 slides
Algebra and Geometry Reasoning: Concepts and Proofs
Explore key concepts in algebra and geometry reasoning, including properties of equality, distributive property, and proofs using deductive reasoning. Practice solving equations, identifying properties of congruence, and writing two-column proofs to justify mathematical statements.
0 views • 13 slides
Comprehensive Mathematics Prior Learning Overview
This comprehensive overview delves into key mathematical concepts, including geometry, equations, quadratics, and circle theorems. It covers topics such as similarity, congruence, vectors, and algebraic manipulation, preparing students for more complex problem-solving and geometric proofs. The conte
0 views • 6 slides
Challenges in Constant-Round Public-Coin Zero-Knowledge Proofs
The paper discusses the implausibility of constant-round public-coin zero-knowledge proofs, exploring the limitations and complexities in achieving them. It delves into the fundamental problem of whether such proofs exist, the challenges in soundness error reduction, and the difficulties in parallel
0 views • 20 slides
Exploring Geometric Probabilities: From Fractions to Integrals
Delve into the realm of geometric probabilities with insights on how to transition from fractions to definite integrals, utilizing technology for enhanced learning experiences. Understand the significance of probability calculations in quantifying likelihood, incorporating geometric representations
0 views • 26 slides
Math Practice: Ratios, Proportions, Estimation, and Geometric Figures
Explore math concepts such as ratios, proportions, estimation, rounding, and geometric figures through engaging lessons and problem-solving scenarios. Practice using proportions to find missing values, round whole numbers and decimals, estimate costs, and learn about geometric shapes. Enhance your m
0 views • 19 slides
Understanding Infinite Geometric Sequences and Convergent Series
Explore the concept of infinite geometric sequences in mathematics through the example of cutting a string into halves. Learn how to identify convergent series and calculate sums to infinity, distinguishing between convergent and divergent series based on the common ratio. Delve into the formula for
0 views • 12 slides
Understanding Geometric and Poisson Probability Distributions
Explore the geometric and Poisson probability distributions, including criteria for geometric random variables, formulas, and practical examples. Learn how to calculate probabilities using the geometric distribution and apply it in scenarios like Russian Roulette and blood donor collection. Dive int
0 views • 13 slides
Overview of Proposed Changes in Producer Price Index Formulas
The U.S. Bureau of Labor Statistics is considering transitioning from a modified Laspeyres formula to a geometric Young formula for elementary indexes in the Producer Price Index (PPI). This proposed change aims to enhance the accuracy and economic relevance of price measurements by utilizing a geom
0 views • 25 slides
Advancements in Interactive Proofs for Efficient Computation
Recent developments in interactive proofs focus on enhancing the efficiency of computations outsourced to untrusted servers, addressing concerns related to correctness and privacy. Solutions like doubly efficient interactive proofs offer a secure way to delegate computations while minimizing relianc
0 views • 25 slides
Understanding Exhaustive Proofs and Proof by Cases in Discrete Math
Exhaustive proofs and proofs by cases are essential methods in discrete mathematics for proving theorems. Exhaustive proofs involve checking all possibilities, while proof by cases focuses on considering different scenarios separately. The methods are illustrated through examples like proving (n+1)^
0 views • 8 slides
Evolution of Proofs in Computer Science
Explore the development of proofs in computer science, from classical mathematical proofs to interactive and zero-knowledge proofs pioneered by researchers like Goldwasser, Micali, Rackoff, and others. Discover how proof theory has evolved over time, making computation verification more efficient an
0 views • 28 slides
Constant Round Interactive Proofs for Delegating Computations
The research explores techniques for securely delegating computations to the cloud, addressing concerns of correctness and privacy through interactive proofs and efficient verification methods. It compares classical and doubly efficient interactive proofs, emphasizing the importance of computational
0 views • 43 slides
Geometric Construction and Geometrical Figures Lecture Images
Explore a series of informative images illustrating geometric construction, types of angles, triangles, and various geometric figures like squares, rectangles, rhombuses, parallelograms, and circles. Enhance your understanding of key geometric concepts with these detailed visuals.
0 views • 14 slides
Geometric Constructions: Mastering Compass and Straight Edge Techniques
Explore the art of geometric constructions using only a compass and straight edge. Learn to bisect angles, construct perpendicular bisectors, draw lines perpendicular to given lines, create parallel lines, divide line segments equally, and more. Equip yourself with the necessary skills and technique
0 views • 11 slides
Evolution of Proofs in Computer Science: Zero-Knowledge Proofs Overview
Explore the evolution of proofs in computer science focusing on succinct zero-knowledge proofs, their significance, and impact on Bitcoin protocol and public ledgers. Learn about classical proofs, zero-knowledge proofs by Goldwasser-Micali-Rackoff, and interactive proofs in the realm of computer sci
0 views • 40 slides
Understanding Predicate Logic and Quantifiers for Symbolic Proofs
Dive into the realm of predicate logic and quantifiers, exploring the nuances of symbolic proofs and evaluating logical statements. Learn about bound variables, domain considerations, and strategies for constructing iron-clad proofs using quantifiers.
0 views • 36 slides
Quantum NIZK Proofs Explained with Dominique Unruh
Explore the concept of non-interactive quantum zero-knowledge proofs with Dominique Unruh at the University of Tartu. Discover how these proofs ensure verifier acceptance of true statements while learning nothing, and delve into the various implementations and implications of Quantum NIZK proofs wit
0 views • 19 slides
Zero-Knowledge Proofs in Cryptography
Exploring zero-knowledge proofs in cryptography, this content delves into interactive protocols, perfect zero-knowledge definitions, and the QR protocol's honest verifier and malicious verifier zero-knowledge theorems. It discusses how simulators work to maintain zero-knowledge properties and the si
0 views • 37 slides
Interactive Proofs in Complexity Theory
Delve into the realm of interactive proofs in complexity theory, exploring concepts such as completeness, soundness, and efficiency. Discover how interactive proof systems can be utilized in scenarios like graph isomorphism and their implications on the complexity classes NP and coNP. Uncover the in
0 views • 40 slides
Predicate Logic and Proofs in CSE 311
Explore the translation of statements into predicate logic, learn about inference proofs and nested quantifiers, and delve into the application of logical thinking in real-world scenarios. Discover a new way of constructing proofs and understand notation laws of inference. Engage in interactive proo
0 views • 37 slides
Understanding Geometric Frustration in Magnetism and Ice
Explore the concept of geometric frustration in magnetism and ice, where energetic requirements cannot be optimized simultaneously. Learn about frustrated magnetic insulators, quantum spin liquids, and the unique properties of geometrically frustrated systems such as triangular and Kagome lattices.
0 views • 25 slides
Geometric Construction in Engineering Drawing: Lecture Highlights
Geometric construction involves creating primitive geometric forms like points, lines, and planes to define objects in space. The lecture covers the basics of 2D geometric primitives, such as points, lines, circles, and arcs. It explains the significance of points and lines in technical drawings and
0 views • 18 slides
Understanding Mathematical Proofs and Concepts
Explore the world of mathematical proofs through chapters 4, 5, and 6. Delve into terminology, theorems, definitions, divisors, and accepted axioms used in mathematical reasoning. Discover the logic behind proofs and various methods employed in establishing the truth of mathematical statements.
1 views • 101 slides