Discrete Math for Computer Science Course - ICS 6D, Spring 2016
Prof. Sandy Irani leads the ICS 6D Discrete Math for Computer Science course at UC Irvine. The course covers various topics in discrete mathematics, with lectures on Mondays, Wednesdays, and Fridays. Teaching assistants and readers support the course, which includes interactive activities on zyBook.
5 views • 32 slides
Discrete Mathematics
Explore the foundations of logic and proofs in discrete mathematics, focusing on compound propositions, bit operations, and applications of propositional logic. Learn about how computers use bits for information representation and manipulation, and delve into translating English sentences into logic
5 views • 15 slides
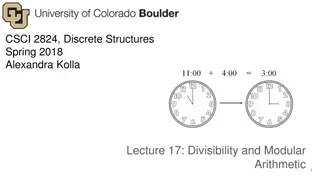
Understanding Divisibility and Modular Arithmetic in Discrete Structures
This lecture discusses the concepts of divisibility and modular arithmetic in the context of discrete structures. It covers definitions, notation, and examples of divisibility by integers, including proving properties such as the divisibility of products and consecutive integers. Through practical e
1 views • 43 slides
Advancements in Discrete Auto Analyzers for Clinical Chemistry Operations
Discrete auto analyzers integrate specimen handling, reagent systems, optical components, and computers for streamlined functionality. The innovation in computer technology, particularly microprocessors, has revolutionized these analyzers, enabling precise data management, liquid handling, and optic
0 views • 17 slides
Microeconometric Modeling with Multinomial Logit Model
The topic discusses the Multinomial Logit Model in the context of discrete choice modeling, covering concepts, models, consumer preferences, utility maximization, and implications for discrete choice models. It explores how consumers maximize utility under budget constraints, the need for well-defin
1 views • 58 slides
Understanding Random Variables and Their Applications in Various Fields
Random variables play a crucial role in statistics, engineering, and business applications. They can be discrete or continuous, depending on the nature of the outcomes. Discrete random variables have countable values, while continuous random variables can take on any real number. This article explor
0 views • 6 slides
Understanding Discrete Optimization in Mathematical Modeling
Discrete Optimization is a field of applied mathematics that uses techniques from combinatorics, graph theory, linear programming, and algorithms to solve optimization problems over discrete structures. This involves creating mathematical models, defining objective functions, decision variables, and
0 views • 12 slides
Understanding Binomial and Poisson Data Analysis
Discrete data, including Binomial and Poisson data, plays a crucial role in statistical analysis. This content explores the nature of discrete data, the concepts of Binomial and Poisson data, assumptions for Binomial distribution, mean, standard deviation, examples, and considerations for charting a
2 views • 31 slides
Noise & Error Shaping in Discrete-Time DSMs EECT 7V88 - Fall 2021
Explore the intricacies of noise and error shaping in DSMs with Professor Y. Chiu's course on Discrete-Time DSMs for EECT 7V88 in Fall 2021. Delve into DAC architectures including Nyquist, binary-weighted, and more. Learn about Binary-Weighted CR DAC, CP Cu, capacitor arrays, gain errors, nonlineari
1 views • 30 slides
Understanding Logical Connectives in Discrete Mathematics
Explore the world of propositional logic and truth tables in discrete mathematics through a peer-instruction approach. Learn about basic logical connectives, new connectives, complex formulas, operator precedence, and the nuances of implication (implies) with engaging examples. Delve into scenarios
0 views • 14 slides
Understanding Boolean Logic and Contrapositive Forms in Discrete Math
Delve into the world of Boolean logic and contrapositive forms in discrete math through topics such as simplifications, DeMorgan's Laws, and conditional operators. Explore how to identify equivalent Boolean expressions and prove contrapositive statements using logical reasoning.
0 views • 22 slides
Understanding Sampling and Signal Processing Fundamentals
Sampling plays a crucial role in converting continuous-time signals into discrete-time signals for processing. This lecture covers periodic sampling, ideal sampling, Fourier transforms, Nyquist-Shannon sampling, and the processing of band-limited signals. It delves into the relationship between peri
1 views • 60 slides
Resolution in Discrete Math: Exercise on Rules of Inference
Using resolution in the context of discrete mathematics, this exercise demonstrates how the hypotheses related to rain, umbrellas, and getting wet are logically connected to show that Yvette does not get wet. The solution breaks down the assumptions and applies resolution to derive the final conclus
0 views • 4 slides
Understanding Direct Proofs in Discrete Mathematics
Explore the principles of direct proof in discrete mathematics through a Peer Instruction approach by Dr. Cynthia Bailey Lee and Dr. Shachar Lovett. Learn how to prove theorems of the form "if p, then q" using logical rules, algebra, and math laws. Utilize a clear template for direct proofs, practic
0 views • 17 slides
Guide to Direct Proofs in Discrete Math
Dive into the world of direct proofs in discrete math with this comprehensive guide. Learn how to prove implications, create truth tables, and follow a step-by-step direct proof template. Test your understanding with engaging quizzes and practical examples. Master the art of logical reasoning and fo
0 views • 18 slides
Discrete Optimization: Fundamentals and Applications
Explore the foundations of discrete optimization in MA2827 with a focus on graph theory, complexity basics, shortest path algorithms, minimum spanning trees, maximum flow, and more. Dive into concepts such as Menger's Theorem, disjoint paths, path packing, and directed graphs. Gain insights into ver
0 views • 34 slides
Understanding Discrete Probability Distributions
Explore the definition of random variables, probability distributions, and three types of discrete distributions - Binomial, Hypergeometric, and Poisson. Learn about the mean, variance, and standard deviation of probability distributions, as well as the difference between discrete and continuous dis
3 views • 32 slides
Rules of Inference in Discrete Math Exercises
In this exercise, two arguments are presented involving logical reasoning in Discrete Mathematics. The solutions explain the application of rules of inference for each step in the arguments. The exercise explores implications and deductions based on given premises to draw valid conclusions.
0 views • 5 slides
Understanding Proof by Contradiction in Discrete Math
Explore the concept of proof by contradiction in discrete math through examples and templates. Learn how to derive contradictions to establish the truth of theorems, with demonstrations on topics like integers being both even and odd. Discover the power of contradictions in challenging assumptions a
0 views • 19 slides
Analyzing Validity of Arguments in Discrete Math
This exercise assesses the validity of arguments in discrete mathematics by identifying logical errors or applying rules of inference. The solutions provided highlight fallacies such as affirming the conclusion, modus tollens, and denying the hypothesis. Understanding these principles is crucial for
0 views • 4 slides
Insights into Graph Colorings, Chromatic Polynomials, and Conjectures in Discrete Geometry
Delve into the fascinating world of graph colorings, chromatic polynomials, and notable conjectures in discrete geometry. Explore the impact of June Huh in bringing Hodge theory to combinatorics and his proof of various mathematical conjectures. Uncover the significance of the four-color theorem, co
0 views • 17 slides
Registration and Purchase Details for MATH 1019 Discrete Mathematics Course
Learn how to register and purchase materials for the MATH 1019 Discrete Mathematics course for Computer Science at Fall 2016. Options include going all-digital with Connect or opting for a loose-leaf print text. Follow the easy steps provided to get started and access course materials. Additionally,
0 views • 9 slides
Peer Instruction in Discrete Mathematics
Explore topics in discrete mathematics such as set sizes, set builder notation, power sets, Cartesian products, unions, intersections, and different ways of defining sets. Learn through engaging visuals and examples presented under a Creative Commons License by Dr. Cynthia Bailey Lee and Dr. Shachar
0 views • 16 slides
Rules of Inference Exercises and Solutions in Discrete Mathematics
Explore exercises and solutions in discrete mathematics focusing on rules of inference. Analyze logical premises and draw relevant conclusions using rules such as modus tollens, modus ponens, and disjunctive syllogism. Understand the application of these rules in different scenarios to reach valid d
0 views • 4 slides
Exploring Discrete Mathematics through Graph Theory
Delve into the world of discrete mathematics with a focus on graph theory. Learn about graphs, their properties, and essential theorems. Discover how graphs model relations in various applications like network routing, GPS guidance, and chemical reaction simulations. Explore graph terminology, theor
0 views • 26 slides
Understanding Logical Connectives "or" in Discrete Mathematics
Explore the concepts of inclusive "or" and exclusive "or" in logical statements through various examples in discrete mathematics. Understand the implications of each interpretation in sentences related to prerequisite courses, incentives, set selection, and school closure due to extreme weather cond
0 views • 5 slides
Peer Instruction in Discrete Mathematics
Explore the world of discrete mathematics with Dr. Cynthia Bailey Lee and Dr. Shachar Lovett through peer instruction. Dive into topics like step-by-step equivalence proofs and the equivalence of logical operators. Discover the different methods to show propositions are equivalent and delve into log
0 views • 14 slides
Introduction to Dynamical Systems Math 319
Dive into the world of dynamical systems with a focus on applications like population growth, radioactive decay, and more. Learn about discrete time steps, multivariable models, and the essence of dynamical systems in tracking changes over time. Explore the simplicity of Euler's Method and the impor
0 views • 65 slides
Discrete Mathematics Learning Goals and Examples in Propositional Logic
Explore the learning goals in discrete mathematics focusing on translating English sentences to propositional logic, evaluating compound propositions, forming converses and contrapositives, and determining consistency. Dive into examples of conditional statements, converse, inverse, contrapositive,
0 views • 14 slides
Understanding Discrete Mathematics: Logic and Reasoning
Explore the fundamentals of mathematical logic, statements, connectives, and truth tables in the context of Discrete Mathematics. Delve into the theory of inference and the uses of logic in various fields such as Computer Science and the Natural Sciences. Gain insights into negation as a connective
0 views • 78 slides
Understanding Combinatorics in Discrete Mathematics
Combinatorics, a key facet of discrete mathematics, explores the arrangement of objects and finds applications in various fields like discrete probability and algorithm analysis. The Rule of Sum, a fundamental principle, dictates how tasks can be accomplished when they cannot be done simultaneously.
0 views • 70 slides
Introduction to Sequential Pattern Mining Overview
Discover the concept of sequential pattern mining, a popular data mining task introduced in 1994, with a focus on analyzing discrete sequences to find interesting patterns. Sequential pattern mining involves finding frequent subsequences in sets of discrete sequences, such as items purchased by cust
1 views • 24 slides
Understanding Valid and Invalid Arguments in Discrete Mathematics
Concepts of valid and invalid arguments in discrete mathematics are explored through examples. Learn how to determine the validity of arguments based on premises and conclusions. Practice using truth tables to evaluate argument forms. Enhance your logical reasoning skills in Discrete Mathematics.
0 views • 22 slides
Discrete Scenarios in Graphs
The scenarios where the height of a student depending on age, time taken in a race depending on distance, number of students taking a test depending on class size, and length of a walkway depending on number of bricks are analyzed to determine which would result in a discrete graph with isolated poi
1 views • 23 slides
Understanding Discrete Random Variables and Variance Relationships
Explore the concepts of independence in random variables, shifting variances, and facts about variance in the context of discrete random variables. Learn about key relationships such as Var(X + Y) = Var(X) + Var(Y) and discover common patterns in the Discrete Random Variable Zoo. Embrace the goal of
0 views • 27 slides
Optimization of Crude Oil Blend Scheduling in Industrial Refineries
Explore a discrete-time model for scheduling optimization in a complex industrial-sized refinery, focusing on feedstock storage assignment and crude blend scheduling. The objective is to study various time steps and unit configurations to maximize efficiency and productivity. Various benchmarks and
0 views • 10 slides
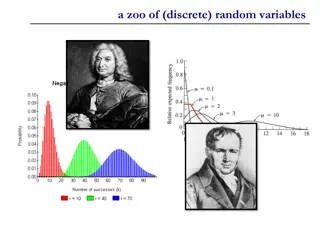
Understanding a Zoo of Discrete Random Variables
Discrete random variables play a crucial role in probability theory and statistics. This content explores three key types: Bernoulli random variable, binomial random variable, and error-correcting codes. From understanding the basics of Bernoulli trials to exploring the application of error correcti
0 views • 27 slides
Discrete Optimization Methods Overview
Discrete optimization methods, such as total enumeration and constraint relaxations, are valuable techniques for solving problems with discrete decision variables. Total enumeration involves exhaustively trying all possibilities to find optimal solutions, while constraint relaxations offer a more tr
0 views • 80 slides
Predicates and Quantifiers Exercise Solutions in Discrete Mathematics
Exercise solutions involving predicates and quantifiers related to printer status, job status, and queueing in a discrete mathematical context. The solutions address scenarios like lost jobs, busy printers, queued jobs, and out-of-service printers. References to textbooks in discrete mathematics are
0 views • 4 slides
Understanding Cyclic Groups and Discrete Logarithms
Exploring the concepts of cyclic groups and discrete logarithms in group theory. This presentation covers the definition of generators, examples of cyclic groups, important theorems related to prime orders and cyclic groups, uniform sampling in cyclic groups, and the discrete logarithm problem. Exam
0 views • 14 slides