Differential white blood cell count
Differential white blood cell count, also known as a leukocyte count, is a crucial test to determine the different types of white blood cells present in the blood. The cells are classified into granulocytes (neutrophils, eosinophils, basophils) and agranulocytes (lymphocytes, monocytes). Blood smear
3 views • 21 slides
Understanding Bernoulli's Equation in Fluid Mechanics
Bernoulli's equation, a fundamental principle in fluid dynamics, relates pressure, kinetic energy, and potential energy of a fluid flowing in a pipe. Through examples and explanations, explore how this equation can be used to calculate velocity, pressure differences, and forces in various scenarios
1 views • 12 slides
Approach to Depression in Primary Care by Dr. Jon Davine
In this presentation, Dr. Jon Davine discusses the approach to depression in primary care, covering topics such as differential diagnosis, antidepressant medication selection, augmentation techniques, and treatment options like ECT and TMS. The sad state is explored through differential diagnoses, i
5 views • 56 slides
Understanding Numerical Methods for Approximating Analytic Equations
Introduction to approximating solutions to analytic equations, focusing on differential equations, integral equations, and integro-differential equations. Exploring ordinary and partial derivatives, differential and integral equations, and the involvement of unknown functions and their derivatives a
2 views • 15 slides
Exploring Genetics and Genomics in Integrative Biology
Delve into the world of genetics and genomics through the lens of integrative biology, investigating the differences between cell types, the rationale for gene expression profiling, and the analysis of differential gene expression in various diseases. Uncover the significance of gene ontology, co-ex
0 views • 22 slides
Understanding Waveguiding Systems and Helmholtz Equation in Microwave Engineering
Waveguiding systems are essential in confining and channeling electromagnetic energy, with examples including rectangular and circular waveguides. The general notation for waveguiding systems involves wave propagation and transverse components. The Helmholtz Equation is a key concept in analyzing el
1 views • 50 slides
Understanding Central Abdominal Pain and Masses in Clinical Practice
Abdominal pain evaluation involves considering various differential diagnoses such as appendicitis, small bowel obstruction, and mesenteric ischemia. By categorizing pain as visceral, parietal, referred, or radiating, healthcare providers can better understand the underlying pathology. The history o
0 views • 57 slides
Differential Equations of First Order & Higher Degree: Lecture 18
This lecture covers differential equations of first order but not of the first degree, general forms of such equations, methods for solving them, and examples of differential equations to be solved. The content includes detailed explanations, equations, solutions, and problem-solving techniques.
0 views • 9 slides
Understanding Thermodynamics and Fluid Mechanics Fundamentals for Efficiency
Explore key concepts in thermodynamics and fluid mechanics such as the equation of continuity, the first law of thermodynamics, the momentum equation, Euler's equation, and more. Learn about efficiency, internal energy, and the laws governing energy transfer in various systems. Delve into topics lik
2 views • 12 slides
Understanding Differential Leucocyte Count for Blood Disorders
Differential Leucocyte Count (DLC) is crucial for diagnosing blood-related disorders by analyzing the distribution and morphology of white blood cells. Dr. Versha Prasad explains the significance, normal values, and various conditions like neutrophilia, lymphocytosis, monocytosis, and basophilia. Th
1 views • 15 slides
Understanding WBC Differential Count in Blood Analysis
WBC (white blood cell) count is essential in assessing a patient's health. A differential count helps determine the percentage of different types of white blood cells. This analysis can provide important insights into various health conditions like infections, allergies, and systemic illnesses. The
1 views • 9 slides
Understanding Myxedema Coma: Symptoms, Diagnosis, and Management
Myxedema coma is a rare, life-threatening condition associated with decompensated hypothyroidism. It presents with altered mental status, low body temperature, and various metabolic abnormalities. This article explores the primary symptoms, differential diagnosis, and management of myxedema coma bas
0 views • 20 slides
Understanding Differential Leveling in Surveying
Differential leveling is a crucial aspect of surveying that involves determining the elevation of points with respect to a reference datum. This process includes various key elements such as benchmark, back sight, fore sight, and change points. By utilizing methods like the Height of Instrument and
1 views • 12 slides
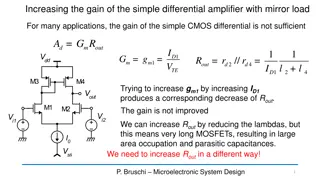
Techniques to Increase Gain in a Simple Differential Amplifier
Explore methods to boost the gain of a simple CMOS differential amplifier by replacing the current mirror with a cascode mirror, adding a common-gate stage, and employing a cascode differential amplifier. These techniques help improve Rout without extensive use of long MOSFETs, optimizing the amplif
2 views • 30 slides
Understanding Differential Equations: Types, Classification, and Solutions
Differential equations are mathematical equations that relate independent and dependent variables through differential coefficients. They can be classified as ordinary or partial, based on the types of derivatives involved. The order and degree of a differential equation, as well as its linearity an
2 views • 26 slides
Understanding the Hammett Equation in Chemical Reactions
The Hammett equation explores how substituents influence the dissociation of benzoic acid, affecting its acidity. By quantifying this influence through a linear free energy relationship, the equation helps predict the impact of substituents on different processes. Through parameter definitions and m
0 views • 9 slides
Understanding Differential Equations in Economics Honours
Differential equations, introduced by Newton and Leibniz in the 17th century, play a key role in economics. These equations involve derivatives and represent implicit functional relationships between variables and their differentials, often related to time functions. The order and degree of a differ
1 views • 16 slides
Introduction to Differential Equations and Laplace Equations
Understanding differential equations of various orders, solving methods, linear and non-linear equations, ordinary and partial differential equations, definitions of solutions, and general vs. particular solutions in the context of Differential Equations and Laplace Equations.
1 views • 20 slides
Introduction to Dynamic Structural Equation Modeling for Intensive Longitudinal Data
Dynamic Structural Equation Modeling (DSEM) is a powerful analytical tool used to analyze intensive longitudinal data, combining multilevel modeling, time series modeling, structural equation modeling, and time-varying effects modeling. By modeling correlations and changes over time at both individu
0 views • 22 slides
Understanding Separation Columns in Chemical Engineering
Explore the world of separation columns including distillation, absorption, and extraction, along with empirical correlations, minimum number of stages, Fenske equation, Underwood equation, Kirkbride equation, examples, and solutions presented by Dr. Kh. Nasrifar from the Department of Chemical and
5 views • 15 slides
Comprehensive Overview of Freezing Time Methods in Dairy Engineering
Neumann, Tao, and Non-Dimensional methods are key approaches for determining freezing times in unsteady state heat transfer processes in dairy engineering. The Neumann Problem, Tao Solutions, and Cleland and Earle Non-Dimensional Equation offer distinct equations and models to calculate freezing tim
1 views • 8 slides
Understanding Differential Equations in Physical Phenomena
Differential equations play a crucial role in modeling physical phenomena involving rates of change like fluid motion, mechanical systems, and heat dissipation. This content explores examples of differential equations in motion and provides insights on sketching direction fields using tools like Map
0 views • 11 slides
Introduction to Quantum Mechanics: Energy Levels and Schrödinger Equation
Quantum mechanics reveals that all systems possess discrete energy levels, determined by solving the Schrödinger equation where the Hamiltonian operator represents total energy. In a particle-in-a-box scenario, potential energy is infinite outside the box. The Schrödinger equation simplifies to a
0 views • 12 slides
Fundamental Comparison: Wheeler-DeWitt vs. Schrödinger Equation
The debate on whether the Wheeler-DeWitt equation is more fundamental than the Schrödinger equation in quantum gravity remains inconclusive. While the Wheeler-DeWitt equation presents an elegant formulation, the Schrödinger equation is essential in specific cases. The issue of time and coordinate
0 views • 6 slides
Exploring SymDiff: A Differential Program Verifier
SymDiff is a platform that leverages program verification to analyze program differences, focusing on differential verification to verify properties of program variances rather than the program itself. The architecture, language subset, and modeling imperative programs/heaps are key components discu
1 views • 18 slides
Understanding Open Channel Flow and Mannings Equation
This review covers hydraulic devices such as orifices, weirs, sluice gates, siphons, and outlets for detention structures. It focuses on open channel flow, including uniform flow and varied flow, and explains how to use Mannings equation for calculations related to water depth, flow area, and veloci
0 views • 43 slides
Exploring Membrane Potential Densities and the Fokker-Planck Equation in Neural Networks
Delve into the concepts of membrane potential densities and the Fokker-Planck Equation in neural networks, covering topics such as integrate-and-fire with stochastic spike arrival, continuity equation for membrane potential density, jump and drift flux, and the intriguing Fokker-Planck Equation.
0 views • 29 slides
Understanding CMRR in Differential Amplifiers
Differential input amplifiers, including operational, instrumentation, and difference amplifiers, play a crucial role in amplifying differential signals while rejecting common-mode noise. The Common-Mode Rejection Ratio (CMRR) is a key parameter in these amplifiers, indicating their ability to suppr
0 views • 48 slides
Applications of Differential Equations in Engineering and Mathematics
Exploring the practical applications of differential equations, specifically focusing on Newton's Law of Cooling and Orthogonal Trajectories. The concept of exact differential equations and their solutions, along with real-life examples demonstrating temperature changes over time, are discussed. Und
0 views • 11 slides
Leapfrog Scheme for Advection Equation
The provided images illustrate the Leapfrog scheme applied to an advection equation, focusing on the center method in time and space. The stability of the method is analyzed with assumptions regarding the behavior of the solution. Through the exploration of Courant numbers and CFL conditions, the st
0 views • 25 slides
Excel Tutorial: Finding Trendline Equation and Calculating Rates of Change
Learn how to find the equation of a trendline in Excel and use it to calculate rates of change. This step-by-step guide includes importing data, adding a trendline, displaying the equation, and interpreting it for analysis. Make the most of Excel's features for data analysis.
0 views • 11 slides
Linearized Boltzmann Equation in Statistical Mechanics
This lecture delves into the linearized Boltzmann equation and its applications in studying transport coefficients. The content covers the systematic approximation of transport coefficients, impact parameters of collisions, and the detailed solution for a dilute gas system. It explores the notation
0 views • 25 slides
Quantum Chemistry Learning Goals and Concepts
This content covers the learning goals and concepts of quantum chemistry leading up to the Schrodinger equation and potential energy wells, excluding the material on the hydrogen atom introduced later. It explores models of the atom, including observations of atomic spectra, the Bohr model, de Brogl
0 views • 22 slides
Analytical Solutions for 2D Heat Equation with Separation of Variables
Consider the steady-state 2D heat equation with constant thermal conductivity. Analyze analytical solutions using separation of variables method for a square plate with defined boundary conditions. Learn how to express the general form of solutions and apply them to the heat equation in Cartesian ge
0 views • 15 slides
Understanding Differential Privacy in Statistical Analysis
Gain insight into the concept of differential privacy in statistical analysis through key terminologies, foundational ideas, and practical examples. Explore the balance between data privacy and statistical quality, and learn how differential privacy serves as a mathematical guarantee to protect indi
1 views • 28 slides
Dynamic Function for Basal Area of Trees Derived from Differential Equation
Mathematical methods presented by Braun and Simmons are used to derive a dynamic function for the basal area of individual trees from a production-theoretically motivated autonomous differential equation. The differential equation and general dynamic function are described, highlighting the relation
0 views • 45 slides
Understanding Partial Differential Equations (PDEs) in Numerical Methods
Explore the world of Partial Differential Equations (PDEs) in the context of numerical methods. Learn about PDE classification, linear and nonlinear PDEs, notation, representing solutions, and applications like the heat equation. Dive into examples and concepts to enhance your understanding.
0 views • 69 slides
Solving Differential Equations: Methods and Techniques
Learn how to solve differential equations using methods like separation of variables and sketch families of solution curves. Understand the process of finding general and particular solutions to equations, and explore a variety of exercises and examples to enhance your understanding. Master the art
0 views • 16 slides
The Challenges of Protecting Privacy with Differential Privacy
The article discusses the motivation behind using differential privacy to protect sensitive data while enabling useful queries. It highlights the promise of differential privacy, challenges faced, attacks on existing systems like PINQ and Airavat, and introduces a defense system called The Fuzz. The
0 views • 24 slides
Analysis and Comparison of Wave Equation Prediction for Propagating Waves
Initial analysis and comparison of the wave equation and asymptotic prediction of a receiver experiment at depth for one-way propagating waves. The study examines the amplitude and information derived from a wave equation migration algorithm and its asymptotic form. The focus is on the prediction of
0 views • 23 slides