Understanding Generalized Heat Engines and Carnot Cycle
Generalized heat engines can be reversible or irreversible, with Carnot engines playing a crucial role in maximizing efficiency. By analyzing the heat absorption and rejection processes, we explore the impact of multiple tiny Carnot engines working together and the overall effect on the main generalized engine's performance.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
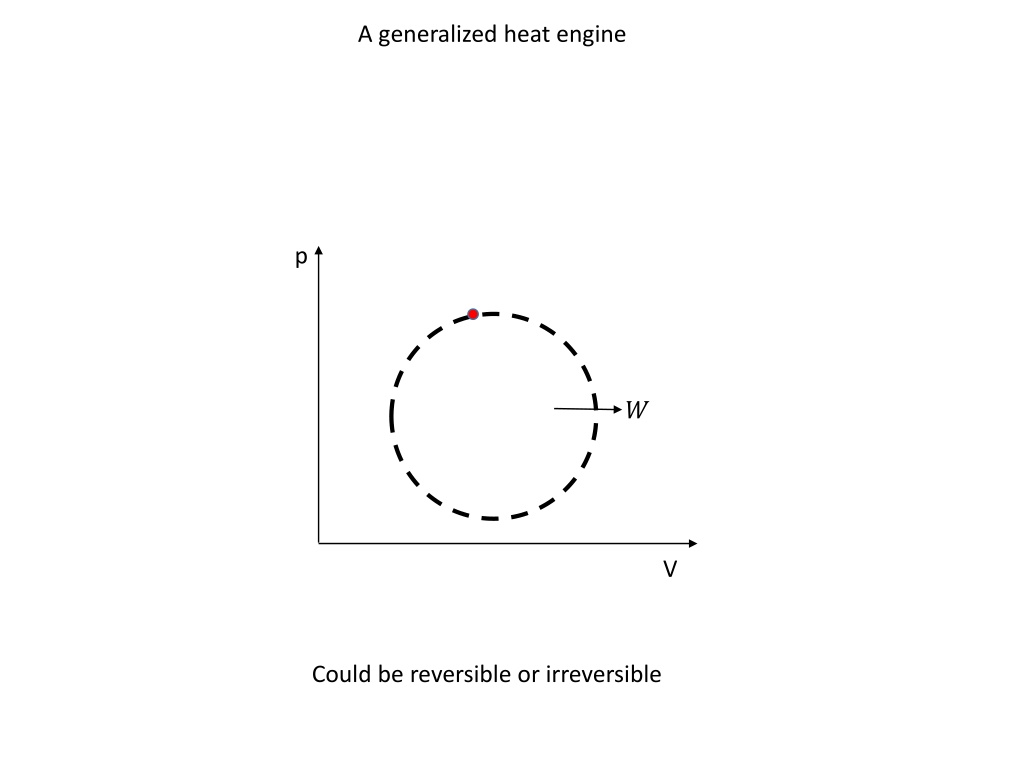
A generalized heat engine p ? V Could be reversible or irreversible
A generalized heat engine ?? ??? ? ??? Absorbs an amount of heat from a body at temperature ?? for an infinitesimal part of the cycle.
Since the work done on/by the gas along the adiabats cancel each other out, bringing them closer to each other reduces the total work done by the Carnot engine. ??,??,?? Isotherm 1 p ??,??,?? Adiabat 2 Adiabat 1 ??,??,?? ??,??,?? Isotherm 2 V
Since the work done on/by the gas along the adiabats cancel each other out, bringing them closer to each other reduces the total work done by the Carnot engine. ??,??,?? Isotherm 1 ??,??,?? p Work done by the gas is then ? = ? + ?? ? = ? ?? (1) ? Adiabat 2 Adiabat 1 ??,??,?? Isotherm 2 ??,??,?? V
A generalized heat engine ? ? ??? ??? ?? ??? ? Set up a Carnot engine which absorbs an amount of heat ? = ?? ?? ?? and rejects heat ?? , does work to the body at temperature ?? (using (1)) = ?? ?? = ?? Adjust the Carnot cycle such that ??
For each narrow Carnot engine: ? ? + ?? = 0 ?? ?? ?? + ?? = 0 ? ?? ?? + ?? ?? = 0 ? ?? ? ?? ?? = ?? 1
A generalized heat engine ? ??? ??? ?? ??? ? In each infinitesimal segment of the engine cycle it absorbs an amount of heat ?? from a body at temperature ?? (?? is different for each segment). For the generalized (reversible) heat engine: ? = ? + ? ? = ? = ? ( ? = 0 for the cycle and ? is the work done by the engine) ? = ? = ?? ?????
?? Work done by all the little Carnot engines = ????? ? ?? 1 Also ?? = ?? ?? ?? ?? = ? ?? ????? ????? ????? ?? ?? ?? = ? ? ????? ????? ?? ?? ?? + ? = ? ????? ????? What is the overall effect of all the little Carnot engines and the main generalized engine? Each Carnot engine absorbs heat ?? + ?? from the reservoir at temperature ? and reject an amount of heat ?? to the body at temperature ??. The main engine absorbs all the heat rejected by the little Carnot engines and produces an amount of work ?.
What is the overall effect of all the little Carnot engines and the main generalized engine? Each Carnot engine absorbs heat ?? + ?? from the reservoir at temperature ? and reject an amount of heat ?? to the body at temperature ??. The main engine absorbs all the heat rejected by the little Carnot engines and produces an amount of work ?. Violates Kelvin-Planck statement of the second law unless the total work done: ?? ?? ?? + ? 0 ? 0 ????? ????? ?? ?? 0 Since ? > 0 ????? ? i.e. Claussius inequality 0 ?
A generalized heat engine ? ??? ??? ?? ??? ?
A generalized heat engine ? ??? ??? ?? ??? ? The Claussius inequality shows that the main engine needs to reject some of the heat it absorbs from the tiny Carnot engines, which means some of the tiny Carnot engines are actually tiny Carnot refrigerators putting some heat back to the reservoir at temperature ?.
A generalized reversible heat engine ? ??? ??? ?? ??? ? Hence, all the heat absorbed from the reservoir at temperature ? by the Carnot engines is put back in the reservoir by the Carnot refrigerators. If the main engine is irreversible, some dissipative work has been done and the total work ????? ?? + ? < 0 whereas, if the main engine is reversible, no dissipative work has been done and ????? ?? + ? = ?
Hence: For a general cycle: ? 0 ? For an irreversible cycle: ? < 0 ? For a reversible cycle: ???? = 0 ?
Arnold Sommerfeld Thermodynamics is a funny subject. The first time you go through it, you don't understand it at all. The second time you go through it, you think you understand it, except for one or two small points. The third time you go through it, you know you don't understand it, but by that time you are so used to it, so it doesn't bother you any more.