Understanding the Carnot Engine: Application of the Second Law of Thermodynamics
Exploring the Carnot engine as an ideal model to understand the Second Law of Thermodynamics, which highlights the efficiency of heat engines and the concept of entropy. The engine operates through a cyclic process, transferring heat from a high-temperature reservoir to a low-temperature one, producing useful work with minimal energy losses. The Carnot cycle, depicted on a temperature-entropy diagram, illustrates the heat transfer and work output principles of this ideal engine.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Thermal Physics Lecture 9 Dr.-Ing. Erwin Sitompul President University http://zitompul.wordpress.com 2 0 1 5 President University Erwin Sitompul Thermal Physics 9/1
Chapter 20 Second Law of Thermodynamics Entropy in the Real World: Engine A heat engine, or more simply, an engine, is a device that extracts energy from its environment in the form of heat and does useful work. At the heart of every engine is a working substance, such as water in steam engine or gasoline-air mixture in automobile engine. For an engine to do work on a sustained basis, the working substance must operate in a cycle; that is, the working substance must pass through a closed series of thermodynamic processes, called strokes, again and again. President University Erwin Sitompul Thermal Physics 9/2
Chapter 20 Second Law of Thermodynamics Entropy in the Real World: Engine Carnot Engine We start studying real engines by analyzing the behavior of an ideal engine. In an ideal engine, all processes are reversible and no wasteful energy transfers occur due to, say, friction and turbulence. We shall focus on a particular ideal engine called Carnot engine, proposed in 1824. This ideal engine turns out to be the best (in principle) at using energy as heat to do useful work. President University Erwin Sitompul Thermal Physics 9/3
Chapter 20 Second Law of Thermodynamics Entropy in the Real World: Engine The next figure shows schematically the operation of a Carnot engine. During each cycle of the engine, the working substance absorbs energy |QH| as heat from a thermal reservoir at constant temperature TH and discharges energy |QL| as heat to a second thermal reservoir at a constant lower temperature TL. The working substance in the engine follows a certain cycle, called the Carnot cycle. Imagine the working substance to be a gas, confined to an insulating cylinder with a weighted, movable piston. At TH, heat |QH| is transferred from the reservoir as the gas undergoes an isothermal expansion from (a) to (b). At TL, heat |QL| is transferred from the working substance to the low-temperature reservoir as the gas undergoes an isothermal compression from (c) to (d). President University Erwin Sitompul Thermal Physics 9/4
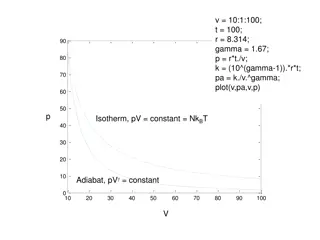
Chapter 20 Second Law of Thermodynamics Entropy in the Real World: Engine The net work per cycle is equal to the area enclosed by the cycle abcda. This work W is performed on some outside object, such as a load to be lifted. As we know, any energy transfer as heat must involve a change in entropy. The plot of Carnot cycle on a temperature-entropy (T-S) diagram is shown below. The two horizontal lines correspond to the two isothermal process of the Carnot cycle. At +QH, S>0, while at QL, S<0. The two vertical lines correspond to the two adiabatic process of the Carnot cycle. Since Q=0, S=0. President University Erwin Sitompul Thermal Physics 9/5
Chapter 20 Second Law of Thermodynamics Entropy in the Real World: Engine The Work. To calculate the net work done by a Carnot engine during a cycle, using the first law of thermodynamics, Eint=Q W, while Eint=0 since the gas will return again and again to any arbitrary state, W Q Q = H L Entropy Change. In a Carnot engine, there are only two reversible energy transfers as heat, and thus two changes in the entropy of the working substance, one at TH and one at TL. The net entropy change per cycle is then: Q Q T T = = + H L S S S H L H L Because entropy is a state function, we must have S=0 for a complete cycle, thus: Q Q T T = H L H L President University Erwin Sitompul Thermal Physics 9/6
Chapter 20 Second Law of Thermodynamics Entropy in the Real World: Engine Efficiency of a Carnot Engine We measure the success of an engine by its thermal efficiency , defined as the work the engine does per cycle divided by the energy it absorbs as heat per cycle: W Q energy we get energy we pay for = = Efficiency, Any Engine H For a Carnot engine, Q Q Q Q = = H L L 1 C Q H H T T = 1 L Efficiency, Carnot Engine C H President University Erwin Sitompul Thermal Physics 9/7
Chapter 20 Second Law of Thermodynamics Entropy in the Real World: Engine Because TL<TH, the Carnot engine necessarily has a thermal efficiency less than unity, less than 100%. Only part of the energy extracted as heat from the high-temperature reservoir is available to do work, and the rest is delivered to the low-temperature reservoir. Later we shall prove, that no real engine can have a thermal efficiency greater than Carnot engine. It is thus impossible to create a perfect engine, in which |QL| is reduced to zero and |QH| is converted completely into work. Through experience, the second law of thermodynamics can be stated in the following alternative version: T T = 1 L C H No series of processes is possible whose sole result is the transfer of energy as heat from a thermal reservoir and the complete conversion of this energy to work There are no perfect engines President University Erwin Sitompul Thermal Physics 9/8
Chapter 20 Second Law of Thermodynamics Entropy in the Real World: Engine Stirling Engine The next figure shows the operating cycle of an ideal Stirling engine. This engine has isothermal heat transfers at temperature TH and TL, both connected by constant-volume processes at Va and Vb. To increase the temperature of the working substance at constant volume reversibly from TL to TH, a transfer of energy as heat Q as heat is required. Also, a reverse transfer is required to decrease the temperature from TH to TL. Several other engines also use 4 steps of different processes in their single cycle. They are called 4-stroke engines: Otto Engine, Brayton Engine, Diesel Engine,and Humphrey Engine. President University Erwin Sitompul Thermal Physics 9/9
Chapter 20 Second Law of Thermodynamics Checkpoint Three Carnot engines operate between reservoir temperatures of (a) 400 and 500 K, (b) 600 and 800 K, and (c) 400 and 600 K. Rank the engines according to their thermal efficiencies, greatest first. (c), (b), and (a) T T = 1 L C H President University Erwin Sitompul Thermal Physics 9/10
Chapter 20 Second Law of Thermodynamics Problem Imagine a Carnot engine that operates between the temperatures TH = 850 K and TL = 300 K. The engine performs 1200 J of work each cycle, which takes 0.25 s. (a) What is the efficiency of this engine? T T 850 300 = = = = 1 0.6471 64.71% L 1 C H (b) What is the average power of this engine? W P t 0.25 1200 = = = 4800 W (c) How much energy |QH| is extracted as heat from the high- temperature reservoir every cycle? 1200 0.6471 W = = = 1854.43J Q H President University Erwin Sitompul Thermal Physics 9/11
Chapter 20 Second Law of Thermodynamics Problem Imagine a Carnot engine that operates between the temperatures TH = 850 K and TL = 300 K. The engine performs 1200 J of work each cycle, which takes 0.25 s. (d) How much energy |QL| is delivered as heat to the low- temperature reservoir every cycle? = = = 1854.43 1200 654.43J Q Q W L H (e) By how much does the entropy of the working substance change as a result of the energy transferred to it from the high- temperature reservoir? From it to the low-temperature reservoir? Q T 1854.43 850 = = = S H 2.18J K H H = 0 S 654.43 300 Q T = 2.18J K = = S L L L President University Erwin Sitompul Thermal Physics 9/12
Chapter 20 Second Law of Thermodynamics Class Group Assignments 1. Consider the Carnot cycle shown below for 0.5 moles of an ideal monatomic gas for which T2 = 500 K, V3 = 2V2, V4 = 1.5V3. The efficiency of a Carnot engine operating on this cycle is: (a) 12% (b) 16% (c) 20% (d) 24% (e) 28% 2. The maximum theoretical efficiency of a Carnot heat engine operating between reservoirs at the steam point and at room temperature is about: (a) 10% (b) 20% (c) 50% (d) 80% (e) 99% 3. A Carnot engine utilizes a heat source at 550 C and has an ideal efficiency of 28%. To increase the ideal efficiency to 35%, what must be the temperature of the heat source? (a) 237 C (b) 327 C (c) 483 C (d) 523 C (e) 638 C President University Erwin Sitompul Thermal Physics 9/13
Chapter 20 Second Law of Thermodynamics Presentation Assignment The followings are a number of invented engine cycles. 1. Otto Cycle 2. Diesel Cycle 3. Stirling Cycle 4. Brayton Cycle 5. Rankine Cycle 6. Atkinson Cycle 26.06.2014 26.06.2014 26.06.2014 03.07.2014 03.07.2014 03.07.2014 Rayhan Darren Herry Dery Hendy Kristiantho Prepare a presentation of about the cycle. Explain the history of the cycle. Present the p-V diagram and/or T-S diagram of the cycle. Give explanations. Explain the advantages and the disadvantages of the cycle. Give examples of applications and implementations of the cycle in real life or mass product. The duration of the presentation is minimum 10 minutes, in order to get maximum point of 3 Extra Points. Send me the presentation file 1 (one) day before the schedule of your presentation, that is 25.06.2014 or 02.07.2014. President University Erwin Sitompul Thermal Physics 9/14
Chapter 20 Second Law of Thermodynamics Homework 9 1.(20-26) 2.(20-30) 3.Group Assignment No.1 Deadline: Wednesday, 25 June 2014. Validation test will be conducted in the beginning of the class. President University Erwin Sitompul Thermal Physics 9/15