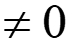Understanding Polynomial Functions and Operations
Polynomial functions are mathematical functions in the form of an expression involving variables and coefficients. They can be manipulated through operations like addition, subtraction, multiplication, and division. Learn about polynomial degrees, identifying polynomials, and performing various operations with polynomials through practical examples.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Polynomial functions: f(x) = 4x3+ 8x2+ 2x + 3, g(x) = 2.5x5+ 5.2x2+ 7, h(x) = 3x2 Polynomial functions are functions that have this form: f(x) = anxn+ an-1xn-1+ ... + a1x + a0, an 0 The value of n must be an nonnegative integer (0, 1, 2, .) The coefficients of each term, an, an-1,..., a1, a0 are real numbers. The degree of the polynomial function is the highest value for n.
Determine the degree of the following polynomials: = x 7+ ( ) 3 2 f x (a) = + 2 5 ( ) 3 2 3 1 g x x x x (b) = ( ) 0 p x (c) Determine whether the functions below are polynomials: 1 ) ( = h x (a) x x = 2+ ( ) 3 h x (b) 1 = ( ) h x (c) 3 = + 2 ( ) h x x x (d)
Operations with polynomials: Addition Example: 1.(2x + 5y) + (3x 2y) = 2x + 5y + 3x 2y = 2x + 3x + 5y 2y = 5x + 3y 2. (3x3 + 3x2 4x + 5) + (x3 2x2 + x 4) = 3x3 + 3x2 4x + 5 + x3 2x2 + x 4 = 3x3 + x3 + 3x2 2x2 4x + x + 5 4 = 4x3 + 1x2 3x + 1 ...or vertically:
Subtraction Simplify(x3 + 3x2 + 5x 4) (3x3 8x2 5x + 6) (x3 + 3x2 + 5x 4) (3x3 8x2 5x + 6) = (x3 + 3x2 + 5x 4) 1(3x3 8x2 5x + 6) = (x3 + 3x2 + 5x 4) 1(3x3) 1 ( 8x2) 1( 5x) 1(6) = x3 + 3x2 + 5x 4 3x3 + 8x2 + 5x 6 = x3 3x3 + 3x2 + 8x2 + 5x + 5x 4 6 = 2x3 + 11x2 + 10x 10
Multiplication (4x2 4x 7)(x + 3) = (4x2 4x 7)(x) + (4x2 4x 7)(3) = 4x2(x) 4x(x) 7(x) + 4x2(3) 4x(3) 7(3) = 4x3 4x2 7x + 12x2 12x 21 = 4x3 4x2 + 12x2 7x 12x 21 = 4x3 + 8x2 19x 21 or you may do it vertically:
Division Case 1: To divide a polynomial by a monomial, we can divide each term by the monomial. 3 4 x + 2 x x Example: Simplify 2 2 2 4 3 x 1 x 3 x x x + 2 4 3 x x = + = + 2 2 2 2 2 2 2 2 2 2 x x 2 2 x
Division Case 2: To divide a polynomial by a more complicated polynomial, factor up to simplify if possible or if not, using the long division method Example: + x + 2 9 + 14 x x 1. Simplify 7 + + + ) 7 + 2 9 + 14 ( 2 x )( + x x x x = = + 2 x 7 7 x
Division Case 3 : When a polynomial a(x), is divided by a non-constant divisor, b(x), the quotient q(x) and the remainder r(x) are defined by the identitiy ( ) ( ) ( x q x b x a = + ) ( ) r x polynomial divisor quotient remainder Degree of a(x) = degree of b(x) + degree of q(x) Degree of r(x) must be less than the degree of b(x) Eg. Divide 3x3 5x2 + 10x 3 by 3x + 1 3x3 5x2 + 10x 3 =(3x+1)(x2 2x+4) 7 degree 3 degree 1 degree 2 degree 0
Please note that the remainder is at least one degree less than the divisor the sum of the degree of quotient and divisor is the degree of the polynomial quotient divisor remainder 3x3 5x2 + 10x 3 =(3x+1)(x2 2x+4) 7
Synthetic Division Most commonly used for linear divisor in the form of x a 2 x Eg. Divide by
Activity Work in groups of 3. Solve the following problems. Time: 10 minutes + + + ) 1 5 5 3 2 2 ( 4 ) 3 8 ( 9 4 7 x x x x x 1. Simplify + + ) 1 5 5 3 2 ( 3 )( 8 9 7 x x x 2. Find 3 x 1 x 2 3 x 3. Use long division to find (i) (ii) + 2 x + 2 2 1
Zeros and Factors of Polynomials Zero (or root) of a polynomial -solution to the equation. Find the zeros of the polynomials below: (a) (b) (c)
Fundamental Theorem of Algebra If is a polynomial of degree n then will have exactly n zeroes, some of which may repeat. -a polynomial of degree 3 will have ____ zeroes/ roots -a polynomial of degree 6 will have ____ zeroes/ roots Eg. = ) 1 + 3 2 2 5 3 ( ( ) 3 x x x x x + = + + ) 1 + 4 3 2 1 ( 1 )( 1 )( x x x x x x x
The Remainder Theorem (for linear divisor only) x t When a polynomial is divided by , (x p ) (t ) p the remainder is the constant . sx t When a polynomial is divided by , ) (x p t p the remainder is the constant . s = + ( ) ( ) t ( ) x ( r ) x p x x t q x r x = + ( ) ( ) ( ) ( ) p x sx q
Example: Find the remainder of p(x) = x3 7x 6 when it is divided by x- 4. Solution: The remainder is p(4) = 43 7(4) 6 = 30.
The Factor Theorem (for linear divisor only) (x ) p For the polynomial , If is a factor of , then . t x x ( = t (x ) ) 0 p p If , then will be a factor of . 0 ) ( = t p t (x ) p (x ) p For the polynomial , t If is a factor of , then . t sx s = 0 (x ) p p s t sx (x ) p t If , then will be a factor of . 0 = p = ( ) ( ) t ( ) x p x x t q x = ( ) ( ) ( ) p x sx q
The Factor Theorem Example: + + 3 2 Find the value of a for which is a factor of ? ) 2 ( x 3 2 x ax x Solution: Using the factor theorem, , 0 ) 2 ( + a = p + = + = 3 2 ) 2 ( 3 ) 2 ( a 2 2 24 4 0 a = 6
The Factor Theorem Find the factors of the following cubic polynomial. ( x p = + 3 2 ) 2 5 6 x x x Solution: , 6 , 2 , 1 3 factors of 6: Working through these factors, eventually we find that ) 3 = + ) 3 ( 5 ) 3 = 3 2 ( 3 ( 2 6 0 p ) 1 = + ) 1 ( 5 ) 1 = 3 2 ( 1 ( 2 6 0 p = ) 2 ( 2 + ) 2 ( 5 = 3 2 ) 2 ( p 2 6 0 = + + ( ) ( 1 )( 2 )( ) 3 p x x x x