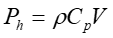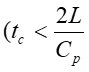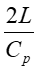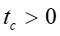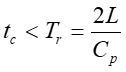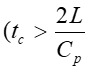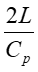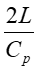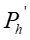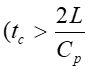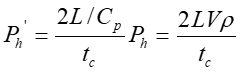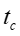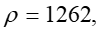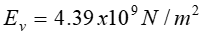Techniques in Fluid Mechanics: Dimensional Analysis
Dimensional analysis is a powerful tool used in engineering to investigate problems in fluid mechanics. By identifying key factors in physical situations, dimensional analysis can establish relationships between them, providing qualitative solutions that can be further refined experimentally. This technique, though not as precise as algebraic analysis, offers valuable insights to understand complex fluid dynamics and behavior during valve closure processes.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
For Instantaneous Valve closure = P C V p h RAPID CLOSURE: 2 L ( t c C p 2 L ) It is physically impossible for a valve to be closed instantaneously. Letus consider a real case where the valve is closed in a finite time tc which is more than zero but less than C p but i.e. 0 ct 2 L = t T c r C p SLOW CLOSURE: 2 L ( t ) Slow closure will be defined as one in which the time of valve movement is greater than c C p 2 L C p Tests have shown that for slow valve closure, i.e. in a time greater than 2 L C p ' hP developed by gradual closure of a valve when 2 L ( t c , the excess pressure produced decreases uniformly from the value at valve to zero at the intake. The water hammer pressure ) is given approximately by C 2 p / L C 2 LV ' p = = P P h h t t c c where ct Ev= = 1262 . 4 , 9 2 39 10 x / N m
Dimensional Analysis: is a useful technique for the investigation of problems in all braches of engineering and particularly in fluid mechanics. If it is possible to identify the factors involved in a physical situation, dimensional analysis can usually establish the form of the relationship between them. The technique does not appear to be as precise as the usual algebraic analysis which seems to provide exact solutions but these are usually obtained by making a series of simplifying assumptions which do not always correspond with the real facts. The qualitative solution obtained by dimensional analysis can usually be converted into a quantitative result determining any unknown factors experimentally. DIMENSIONS: Any physical situation whether it involves a single object or a complete system can be described in
