Strong Average-Case Circuit Lower Bounds: A Brief Overview
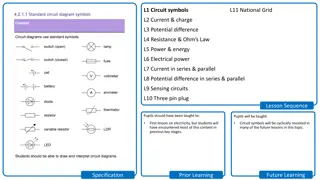
Exploring the history and motivation behind the Circuit Lower Bounds Program focused on proving complexity class separations through non-trivial derandomization, with a primary emphasis on Strong Average-Case Lower Bounds. Ren and Chen delve into the pursuit to establish ?? ≠ ? since the 1980s.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Strong Average-Case Circuit Lower Bounds from Non-trivial Derandomization Hanlin Ren IIIS, Tsinghua Lijie Chen MIT
(Oversimplified) History and Motivation The Circuit Lower Bounds Program for ?? ? Since 1980s, people wanted to prove ?? ?via proving lower bounds for stronger and stronger circuit classes Frontier I: Stronger average-case circuit lower bounds for ???? Frontier II: Super-polynomial lower bounds for ??? ??? The Pseudorandom Generator (PRG) Program for ? = ??? Since 1980s, people wanted to prove ? = ???via constructing PRGs for stronger and stronger circuit classes Frontier I: Strong Average-case lower bounds for ??? Frontier II: Do we really have to use PRGs? Is Black-box derand. equivalent to White-box derand.?
(Oversimplified) History and Motivation The Circuit Lower Bounds Program for ?? ? Since 1980s, people wanted to prove ?? ?via proving lower bounds for stronger and stronger circuit classes Frontier I: Stronger average-case circuit lower bounds for ???? Frontier II: Super-polynomial lower bounds for ??? ??? The Pseudorandom Generator (PRG) Program for ? = ??? Since 1980s, people wanted to prove ? = ???via constructing PRGs for stronger and stronger circuit classes Frontier I: Strong Average-case lower bounds for ???[ ] Frontier II: Is Black-box derand. equivalent to White-box derand.?
The Circuit Lower Bounds Program for ?? ? (Oversimplified) History: Part 1 People wanted circuit lower bounds (and ? ??), but now we know it is HARD But it seemed not that hard in 1980s Quest at that time: understand the constant depth circuits first! ???: constant depth, AND/OR/NOT circuits (unbounded fan-in) [Ajt83,FSS84,Yao85,Has89] Strong lower bounds for ??0 The hard function: Parity! Parity: outputs 1 number of 1 in the input is odd
The Circuit Lower Bounds Program for ?? ? (Oversimplified) History: Part 2 Back in 1980s OK, now we know parity is hard for ???(constant-depth, AND/OR/NOT). Let us make ??? stronger, what about adding parity gates to ???? Philosophy: strengthen the circuit class ``just a little bit by adding the most simple function it cannot compute as available gates. Hopefully, we can get to general circuits very soon! ???? : ??0 extended with ??? ?gates ???[?]: outputs 1 ? does not divide the number of ones in the input [Raz87,Smo87] Strong lower bounds for ???[p] for a prime ?. The hard function for ???? is ??? 3 !
The Circuit Lower Bounds Program for ?? ? (Oversimplified) History: Part 3 Back in 1980s Nice, so far everything has been very successful! Now we know ???[3] is hard for ??02 (constant-depth, AND/OR/NOT/PARITY). ??0 add parity ??0[2] Let us make ??0[2] a little bit stronger. What about adding ???[3] gates to ??0[2]? add ???[3] ??0[6] Shouldn t be that much harder to prove lower bounds for the new class ? Umm
The Circuit Lower Bounds Program for ?? ? (Oversimplified) History: Part 4 The villain The villain ??0[6] (or ??0[?] for a composite ?) ??0? : (constant-depth, AND/OR/NOT/???[?]). Since then, things went downhill. It seemed very hard to prove lower bounds for ???[?] Indeed, it was open for a long time that whether ???? (Non-deterministic Exponential Time) has polynomial-size ??06 circuit of depth 3!
The Circuit Lower Bounds Program for ?? ? NEXP ???? ???? ??0? : (constant-depth, AND/OR/NOT/???[?]). ???0: the union of ??0[?] for all constants ?. In 2011, R. Williams proved that ???? does not have polynomial-size ???0circuits. Theoretical Importance of this result Crossing all the barriers Relativization Algebrization Natural Proofs Proof Techniques Algorithmic Method Cook-Levin Theorem ?? = ?????? Hardness vs. Randomness Time Hierarchy Theorems
The Circuit Lower Bounds Program for ?? ? NEXP ???? In 2011, R. Williams proved that ???? does not have polynomial-size ???0circuits A Big Breakthrough Still, it has some drawbacks comparing to previous lower bounds Only worst-case lower bounds NEXP is gigantic (we want ??) Previous lower bounds can often be adapted to the average-case setting Previous lower bounds are for easy functions in P, like parity or majority Average-case lower bounds can have more applications
The Circuit Lower Bounds Program for ?? ? Subsequent Developments In 2012, R. Williams: ???? ?????? does not have polynomial-size ???0circuits. (make ????a bit smaller) In 2017, R.Chen, Oliveira and Santhanam: ???? cannot be ?+ ?/???????(?)approximated by polynomial-size ???0 circuits. (extend to average-case) ? Technicality The ???? ?????? and ??? ????? lower bounds requires one bit of advice In 2018, Murray and R. Williams: ??? (non-deterministic 2???????(?) time) does not have polynomial-size ???0 circuits. (make ????much smaller) improved? Can this be In 2019, C.: ??? (non-deterministic 2???????(?) time) cannot be ?+ ?/???????(?)approximated by polynomial-size ???0 circuits. The same for ??? ????? (improving all the above) ?
(Oversimplified) History and Motivation The Circuit Lower Bounds Program for ?? ? Since 1980s, people wanted to prove ?? ? via proving lower bounds for stronger and stronger circuit classes Frontier I: Stronger average-case circuit lower bounds for ???? Frontier II: Super-polynomial lower bounds for ??? ??? The Pseudorandom Generator (PRG) Program for ? = ??? Since 1980s, people wanted to prove ? = ??? via constructing PRGs for stronger and stronger circuit classes Frontier I: No Strong Average-case lower bounds for ???[ ] Frontier II: Is Black-box derand. equivalent to White-box derand.?
The Pseudorandom Generator Program for ? = ??? (Oversimplified) History ???(??) fools randomized algorithm ? on ?-bit inputs. PRG ? bits ? bits ? in ?? deterministic time For this, we need to have a PRG for ?/???? (poly-size, unrestricted circuits) with ?(??? ?)-seed length People wanted to show ? = ???by building PRGs for stronger and stronger circuits classes But currently we don t even have PRGs for ??? with ??(?) seed length!
The Pseudorandom Generator Program for ? = ??? Pseudorandom Generators fooling ??? ? We have PRGs fooling ??0 circuits with ??????? ? seed length [Nisan 91; Servedio-Tan 19], but the best PRG fooling ??0 needs seed length > 0.99? [Fefferman-Shaltiel-Umans-Viola 13] Reason: don t have strong enough average-case lower bounds against ??? ! Nisan-Wigderson 94: given a function that cannot be ? ?-approximated by ??0 , we can construct a PRG with ? output bits that ?-fools ??0 Nisan-Wigderson 94: we need a hard function that cannot 1 2+ ? -approximated by ??0 , at least for ? < 1 2+ be 1 ?.
The Pseudorandom Generator Program for ? = ??? Pseudorandom Generators fooling ??? ? State-of-the-art average-case lower bound: ? ?+ ? ?.??-approximated by ??? circuits. This lower bound does not yield PRGs! MAJORITY cannot be In fact, (before this work) it s consistent that ???(a gigantic class that includes ????) ? ?+ ? ?-approximated by (poly-size) ??? circuits! can be ? ?+ ? It s also consistent that ???can be ?-approximated by log? -degree ?2-polynomials. Nisan-Wigderson 94: we need a hard function that is not 1 2+ ? -approximated by ??? , at least for ? < 1 ?.
This Work: Strong Average-Case Lower Bounds for ???? Improved the 1 1/???????(?) result in [C. 19] 2+ NQP (non-deterministic ????????(?) time) 1 2+ 1/????(?) -approximated by polynomial-size ???? circuits. cannot be Surpassed the The same holds for ??? ?????with one bit of advice. 1 2+ 1/ ?-barrier for ??0[ ]
Strong Average-Case Lower Bounds From Non-trivial Derandomization It is in ? under the widely believed conjecture promise? = ?????????? CIRCUIT ACCEPTANCE PROBABILITY PROBLEM (CAPP) Given a circuit ? on ? bits of size ?, estimate Pr ?? ? = 1 within an additive error of 1/? Theorem 2? ??-time CAPP for 2??-size ? circuits ??? cannot be 2+ 1/????(?) -approximated by ?. (Similar results for ?? and ?? (fixed-polynomial)) 1
The Circuit Lower Bounds Program for ?? ? THR THR Circuits THR gates : ? ? = ? ? ?? ??, ? ?. Potential Approach in this Talk! MAJ gates : when ?? s and ? are bounded by poly(n). Frontier Open Questions: Is NEXP ??? ???? Is NEXP ??? ??? ???? THR THR: We can also define ??? ??? ??? ??? ??? ??? THR Note: ??? ??? ??? ??? ??? THR THR THR Exponential Lower Bounds are known!
Strong Average-Case Lower Bounds for ???? ??? [Williams 14] Non-trivial derandomization for ???0 ??? circuits (???0 circuits extended with a bottom layer of ??? gates) Does ??? ???0 contain ???? If so, we already have ??? ??? lower bounds! Cor 1 2+ 1/????(?) -approximated by polynomial-size NQP cannot be ???? ???circuits. Consequently, ??? cannot be computed by ??? ???? ???circuits (very close to ??? ???!) (??0 ??? contains ???) The same holds for ??? ?????with one bit of advice.
Potential Approach to ??? ??? ??? Lower Bounds If there is a 2?/??(1)-time derandomization for ??? ???, Then NEXP not in ??? ??? ???. Can we mine any non-trivial derandomization algorithms from the exponential lower bound proofs for ??? ???or ??? ???? Would imply NEXP not in ??? ??? ???!
Application Black-box and White-box Derandomization Building PRGs seems hard, so why stick to them? PRG does not ``look at the given circuit (Black-box derand.) Maybe looking at the given circuit helps? What about White-box derandomization? [Impagliazzo-Kabanets-Wigderson 02] In certain settings, Looking into the circuit does not help for ?/????! Equivalent sub-exp-time white-box Derandomization of ?/???? sub-exp-time black-box Derandomization of ?/???? Conditions apply: Infinite-Often, with ?? advice, non-deterministic
Black-box and White-box Derand Equivalence for All Circuit Classes We proved that non-trivial white-box derandomization Implies strong average-case lower bounds, which further implies PRGs Some small technical conditions Corollary In certain settings, Looking into the circuit does nothelp for all circuit classes ?! Equivalent sub-exp-time white-box Derandomization of ? sub-exp-time black-box Derandomization of ? Conditions apply: Infinite-Often, with ?? advice, non-deterministic
How this Work relies on recent works ``Almost almost everywhere (a.a.e.) ?? circuit lower bounds [Murray and Williams 2018] Applying PCP of Proximity to help derandomization [C. and Williams 2019] Average-case a.a.e. MA circuit lower bounds [C. 2019]
Line of works [Wil 10] [Wil 11] 2? ??-time algorithm for CAPP of 2? ??-size ???0 circuits Conditional i.o. NPRG for ?/???? Today s Plan [MW 18] [Wil 13] ([Wil 11]) Conditional a.e. MA lower bounds, and ???? ???0. a.a.e. MA lower bounds, and ??? ???0. Give a roadmap and a perspective on all these works [C.W 19] CAPP for approximate sum of ???0 Derandomization Based on Circuit Lower Bounds via [C.R 20] [C. 19] Conditional i.o. NPRG for ??1 Conditional collapse from ??1 to approx. sum of ???0 ???can t be 1 2+ 1/???? ? approximated by ???0 Conditional i.o. NPRG for ??1 a.a.e. MA average-case lower bounds, Conditional collapse from ??1 to ???0 ???can t be 1 2+ 1/??????? ? approximated by ???0 PCP of Proximity pushing evaluations to oracles
Why Average-Case Lower Bounds are Harder? [MW 18] s Worst-Case Lower Bound for NQP Assume ??? ???0 Apply Easy-Witness Lemma, every ??? verifier has polynomial-size ???0 witnesses Easy Witness Lemma ??? ???0 All verifiers ? for ? ??? have ???0 succinct witnesses. Use that and a non-trivial algorithm to contradict non- deterministic-time hierarchy! That is, ``something follows from ??? ???0, which is crucial for the proof
Alternative Plan for Average-case? Assume ??? can be approximated by ???0 circuits Problematic Apply Easy-Witness Lemma(?), every ??? verifier has polynomial-size ???0 witnesses Can we show an average-case easy- witness lemma ? (??? can be approximated by ???0 ??? has ???0 succinct witnesses) Use that and a non-trivial algorithm to contradict non- deterministic-time hierarchy! The old proof breaks
Chen-Oliveira-Santhanams approach: NEXP is average-case hard for ???? [COS 18]: Well, let us bypass this issue with a big weapon: Worst-case to Average-case Hardness Amplification Start with [Wil 14]: ? ???? ??????/1 is (worst-case) hard for ???0. Idea: compute the error correcting code of the entire truth-table of ?, and make it the truth-table of new language ?. Then ? is avg-case hard for ???0. Issue: this requires at least exponential time! Even if ? (??? ?????), ? will notbe in ??? anymore
[COS18]: NEXP is average-case hard for ???? However, even for ??, [COS 18] can only give ? ?+ ? ?(?)-inapproximability bounds The complexity of local-list- decoder To obtain a contradiction, we need ?? is still in ???0! If ? can be approximated by an ???0 circuit ?, we can use a local-decoder ? to correct the error. Now ?? computes ? in the worst case, contradiction! [SV 10, Grinberg-Shaltiel-Viola 18] If D can correct 1 at least as powerful as majority 2 ? ?-error, then ? is
Difficulties with previous approaches That is, we need to prove an average-case lower bound directly, without going through either Hardness Amplification Reason I (requires at least exp-time) Hardness Amplification Reason II (requires majority in decoder) Easy-witness Lemma (we don t have that in average case) So use a more direct approach! Combining MA lower bounds and (nondeterministic) PRGs
Circuit Lower Bounds and Derandomization MA Algorithm NP with a randomized verifier! [BFT 98] ????? is not in P/poly Promise-P = Promise-BPP ?????= NEXP, so ???? not in ?/????. Given an input ?, guess some witness ?, toss some coins ?. ? ? ?Pr ?? ?,?,? = 1 2/3; ?? ?,?,? = 1 1/3 . ? ? ?Pr Pessimistic View Derandomization is hard MATIME[T(n)]: A(x, y, r) runs in T(|x|) time. ??=??????[????(?)] Optimistic View Let us do derandomization!
How to Derandomize Merlin-Arthur Merlin-Arthur Algorithm Given an input ?, guess some witness ?, toss some coins ?. ? ? ?Pr ?? ?,?,? = 1 2/3; ? ? ?Pr ?? ?,?,? = 1 1/3. Derandomization of Merlin-Arthur Given ?, guess ?, estimate Pr ?? ?,?,? = 1 deterministically, and accept if it s > 1/2 If ?????????? = ????????, then ?? = ??! (?????=NEXP as well)
Average-Case? [Buhrman-Fortnow-Thierauf 98] (adapted) ????? cannot be 1 2+ 1/????(?)-approximated by P/poly. Case II Case I Otherwise, using the random-self-reducible EXP- complete language, ??? = ?/???? ?? = ??? ?????= ????[22?] ?/???? If ??? cannot be 1 approximated by ?/????. DONE 2+ 1/????(?)- If Promise-BPP = Promise-P, then NEXP = MAEXP, so NEXP cannot be 1 2+ ????(?)-approximated by P/poly! Therefore, derandomization directly gives average-case lower bounds!
Circuit Lower Bounds for MA are Known, even for average-case [Buhrman-Fortnow-Thierauf 98] ?????can t be ? ?+ ?/????(?)-approximated by P/poly. [Santhanam 09] ??/?can t be ? ?+ ? ?-approximated by SIZE[??] for any ?.
Derandomizing Merlin-Arthur yields Average-Case Circuit Lower Bounds Derandomization of Merlin-Arthur Given ?, guess ?, estimate Pr ?? ?,?,? = 1 deterministically, and accept if it s > 1/2 [Santhanam 09] ??/?can t be ? ?+ ? ?-approximated by SIZE[??] for any ?. If Promise-BPP is in P, then ??can t be approx. by SIZE[??]. If Promise-BPP is in ????[????????(?)], then NQP can t be approx. by ?/????. Sad Reality: derandomization is super hard Can we relax our condition?
Observation I: NPRG suffices! MA Algorithm (NP with a randomized verifier!) Given an input ?, guess some witness ?, toss some coins ?. Nondeterministic PRG Given input 1?, guess a witness ? first. either rejects w and STOP, or takes a seed and computes a PRG ? ? ?Pr ?? ?,?,? = 1 2/3; ?? ?,?,? = 1 1/3. ? ? ?Pr Derandomization of MA with NPRG We can apply NPRG to derandomize MA to NP! Given input ? ( ? = ?), we guess both ? and ?, if NPRG accepts ?, use it to estimate Pr r[? ?,?,? = 1]! (and accept only if 1/2).
Observation II: Conditional Construction suffices! To show ??? not in ? It suffices to prove, assuming ??? in ?, one can construct a polylog(n) seed length NPRG.
Bootstrapping of Derandomization to NPRG How to get it? So, looks like we Circuit Lower Bounds! should have ??? ???0 back in 2011? conditional NPRG [Wil 10] Bootstrapping 2? ??-time Algorithm for CAPP of 2?? circuits ???????(?) seed-length NPRG! [Wil 11] 2? ??-time algorithm for CAPP of 2??-size ???0 circuits! Caveat 1. The resulting NPRG only works infinite-often 2. Bootstrapping only works for general circuits
Conditional Construction of NPRG We only have a 2? ??-time Algorithm for CAPP of 2??-size ???? circuits (the bootstrapping theorem requires such an algorithm for general circuits) Since we can assume ??? ???0 (for proving worst-case lower bound), ?/???? collapses to ????. Intuition Due to the collapse, we can then pretend the 2? ??-time CAPP algorithm works for 2??-size general circuits!
Issue: i.o. NPRG vs MA lower bounds ?? not in ????(??) says that there the hard language ? is not in ????(??)on an infinite number of input lengths What if our infinite-often NPRG does not work for these input lengths? we need an ?? hard language ? which is hard on all input lengths (a.e.)! However, this is an annoying open question. ? ?? ???? G
Partial Solution: Conditional A.E. MA Lower Bounds [Williams 2013], [IKW 02] Assuming ???? ?/????, ?? = ??? = ????[IKW 02], and This is viewpoint is mostly from Natural Proofs versus Derandomization [STOC, 2013] ??????? = ????[22???????(?)] not in P/poly, a.e. which is very different from the famous Non-Uniform ACC Circuit Lower Bounds [CCC, 2011] Under the assumption we want to disprove (???? ???0 ?? = ??? = ????), We have a.e. MA lower bounds Unfortunately, this only works for lower bounds against ???? This is the major reason why previous proof only works for NEXP
Full Solution: a.a.e. MA Lower Bounds [Murray-Williams 2018] Key Observation Each ``good length of the NPRG can be used to derandomize an interval of input lengths of the MA language [MW 18] For a ???????(?)-seed length NPRG G, the interval could be of quasi- polynomial stretch. proved such a lower bound Almost Almost-Everywhere MA lower bounds Informally, for all ?, there is ? [?,????????(?)] such that ? is hard on input length ?.
[MW18]: Apply conditional NPRG to derandomize circuit lower bounds for MA [Wil 10] 2? ??-time Algorithm for CAPP of 2?? circuits ???????(?) seed-length NPRG! [MW 18] [Wil 11] 2? ??-time algorithm for CAPP of 2??-size ???0 circuits! Almost almost-everywhere MA circuit lower bounds Conditional i.o. NPRG Assuming ??? ???0, polylog(n) seed NPRG for general circuits. NQP not in ????!
Adaptation to the Average-Case Worst-Case Lower Bounds a.a.e. MA lower bounds + conditional i.o. NPRG Two New Pieces a.a.e average-case MA circuit lower bounds Polylog(n) seed-length conditional NPRG [C., 2019]
Conditional Construction of NPRG: Adapted [Wil 10] 2? ??-time Algorithm for CAPP of 2?? circuits ???????(?) seed-length NPRG! Bootstrapping only works with ?/???? In the worst-case lower bound, we use the assumption ??? ???0, which implies ?/???? collapses to ???0, and then we can pretend we have algorithms for ?/poly. Solution Indeed, bootstrapping also works for ??1 (circuits of ?(log?) depth)! ??? can be approximated by ???0 ??1 collapses to ???0
[C.19]s Approach in Three Steps Step I: (Conditional Simulation) Assuming ??? can be 0.99-approximated by ???0, ??? can be simulated by ????. Step II: (An NPRG for ???) Since ??1= ???0, now we can pretend we have non- trivial algorithms for ??1, use bootstrapping to get polylog(n) seed length NPRG for ??1. Step III: (The Lower Bound) Prove that there is a language ? in ??????[2???????(?)] such that ? cannot be of Step II to derandomize ? in ???. Contradiction! 1 2+ ? ?-approximated by ??1. Apply NPRG
The Bottleneck of [C.19] Step I (?): (Conditional Simulation) Assuming ??? can be (1 ??? can be simulated by ????? 1 2+ ? ?- Now, suppose we want to prove ??? cannot be approximated by ???0 instead, which steps break? 2+ ? ?)-approximated by ???0, Step II: (An NPRG for ???) not affected! Since ??1= ???0, now we can pretend we have non- trivial algorithms for ??1, use bootstrapping to get polylog(n) seed length NPRG for ??1. The problem is Step I! Step III: (The Lower Bound) Prove that there is a language ? in ???? such that ? cannot be 1 2+ ? ?-approximated by ??1. Apply NPRG of Step II to derandomize ? in ???. Contradiction!
Collapse Theorem The Question 1 2+ ? -approximated by ???0, Assuming ??? can be how do we show a collapse from ??1 to ???0? Idea: Random Self-Reducibility Consider a random self-reducible ??1-complete language ?. That is, there is an error corrector ? such that, if ? computes ? on a of inputs, then ?? computes ? exactly. 1 2+ ? -fraction
The Collapse Theorem in [C.19] The Question Assuming ??? can be 0.99-approximated by ???0, how do we show a collapse from ??1 to ???0? Error Correction in ??? There is an ??1-complete language ? with an ??0 error corrector ?, such that if ? can be 0.99-approximated by ?, then ?? computes ? exactly. If ? can be ?.??- approximated by ????. Then ??? collapses to ????.
The Key Issue on Improving [C.19] The Updated Question Assuming ??? can be how do we show a collapse from ??1 to ???0? 1 2+ ? ?-approximated by ???0, Circuit Complexity of Error Correction Now we need an error corrector corrects 1 2 ? ? error. Typically, such an error corrector requires MAJORITY. ? ?+ ? ?- If ? can be approximated by ????. Then ??? collapses to ??? ????. We don t know how to do circuit-analysis on ??? ???0
Approximate Sum Let ? be a circuit class. A Linear Sum of ? is ? = ?1 ?1+ ?2 ?2+ + ?? ?? where ?? , and ?? ?. ?,? 1 ?,1 + ? if ? ? = 1 if ? ? = 0 We say ?: 0,1? {0,1} is an approximate (linear) sum of ?, if there is an ? as above such that ? ? ? ? ?1 ?? ? for all ?. ?2 ?1 ?2 ?? For example, a function ?: 0,1? {0,1}, has approximate degree ?, iff it is an approximate linear sum of ??? functions on ? bits.
Error Correction with Approximate Sum Lemma There is an ??1-hard language with an approximate sum error corrector! (From Cryptography in ??? [Applebaum-Ishai-Kushilevitz]) Cor 1 2+ ? ?- If ? can be approximated by ???0. Then ??1 collapses to Approximate Sum of ???0