Vibrational Spectrum in Diatomic Chain Structures: Analysis and Eigenmodes
V
i
b
r
a
t
i
o
n
a
l
s
p
e
c
t
r
u
m
f
o
r
s
t
r
u
c
t
u
r
e
s
w
i
t
h
2
a
t
o
m
s
/
p
r
i
m
i
t
i
v
e
b
a
s
i
s
Linear diatomic chain:
2n
2n+1
2n+2
2n-1
2n-2
2a
Equation of motion for atoms on even positions
:
Equation of motion for atoms on odd positions
:
Solution with:
and
Note different
convention for a
than Kittel. I have
a good reason!
Only the labeling convenient is different from monatomic.
If that’s all, why might this be any different from monatomic?
Why should we label it differently?
2
2
What happens?
2
=C
C
Show video
Transverse
acoustic
mode for
diatomic chain
A/B=1
Technically
longitudinal
only in 1D
Transverse
optical
mode for
diatomic chain
Transverse
acoustic
mode for
diatomic chain
Amplitudes
of different
atoms
A/B=-m/M
A/B=1
Technically
longitudinal
only in 1D
Longitudinal Eigenmodes in 1D
Optical Mode:
These
atoms,
if oppositely
charged
, would form an
oscillating dipole which
would couple to optical
fields with
λ
~a
What if the atoms were opposite charged?
Phonon Dispersion in 3D
•
The 1D model can be extended
to 3D if the variables
u
refer
not to displacements of atoms
but planes of atoms.
1
D
m
o
d
e
l
3
D
m
o
d
e
l
Phonon Dispersion in 3D
•
The 1D model can be extended
to 3D if the variables
u
refer
not to displacements of atoms
but planes of atoms.
•
Need to include motions that
are perpendicular to the wave
vector.
1
D
m
o
d
e
l
3
D
m
o
d
e
l
Phonon Dispersion in 3D
•
The 1D model can be extended
to 3D if the variables
u
refer
not to displacements of atoms
but planes of atoms.
•
Need to include motions that
are perpendicular to the wave
vector.
•
These are called
transverse
acoustic modes
(TA), as
opposed to
longitudinal
acoustic modes
(LA).
1
D
m
o
d
e
l
3
D
m
o
d
e
l
Every 3D crystal
has 3 acoustic
branches, 1
longitudinal and 2
transverse
Are the branches
degenerate?
“
P
r
i
m
a
r
y
w
a
v
e
”
=
f
a
s
t
e
r
w
a
v
e
L
A
“
S
e
c
o
n
d
a
r
y
w
a
v
e
”
=
s
l
o
w
e
r
w
a
v
e
T
A
3D Dispersion curves
E
x
a
m
p
l
e
:
E
a
r
t
h
q
u
a
k
e
w
a
v
e
s
No, the perpendicular
displacements will have
different force (“spring”)
constants from the
longitudinal force
constants.
Would you expect the two
transverse branches to be
degenerate?
Think about a tetragonal lattice to debate this.
Number and Type of Branches
•
Every crystal has 3 acoustic
branches, 1 longitudinal and 2
transverse
•
Every additional atom in the
primitive basis contributes 3
further optical branches (again
2 transverse and 1 longitudinal)
3 acoustic branches
+ 3(p-1) optical branches
= 3p branches
1LA +2TA
(p-1)LO +2(p-1)TO
Sometimes transverse will be degenerate
H
o
w
w
o
u
l
d
y
o
u
k
n
o
w
w
h
i
c
h
b
r
a
n
c
h
i
s
l
o
n
g
i
t
u
d
i
n
a
l
?
How many branches and of what type for a perovskite ABO
3
?
2D Square Lattice
Write down the
equation(s) of motion and
guess solution
2D Square Lattice
U
lm
U
l+1,m
U
l,m-1
U
l,m+1
U
l-1,m
•
Write down the
equation(s) of motion
and guess solution
•
How will ṻ relate to u?
How would you add in second
nearest neighbor interactions?
2D Lattice
K
U
lm
U
l+1,m
U
l,m-1
U
l,m+1
U
l-1,m
Compare to 1D solution:
2D Lattice
K
U
lm
U
l+1,m
U
l,m-1
U
l,m+1
U
l-1,m
Compare to 1D solution:
How do you think
you might change
this if a rectangular
lattice?
2D Lattice
K
U
lm
U
l+1,m
U
l,m-1
U
l,m+1
U
l-1,m
Plot
w vs k
for the
[10]
and
[11]
directions.
Identify the values of
at
k=0 and at the BZ edges.
(Hint: draw the BZ first)
2D Lattice
K
U
lm
U
l+1,m
U
l,m-1
U
l-1,m
Plot
w vs k
for the
[10]
and
[11]
directions.
Identify the values of
at
k=0 and at the BZ edges.
(Hint: draw the BZ first)
K
U
lm
U
l+1,m
U
l,m-1
U
l-1,m
Plot
w vs k
for the
[10]
and
[11]
directions.
Identify the values of
at
k=0 and at the BZ edges.
(Hint: draw the BZ first)
Real Phonon
Spectra Might
Look Slightly
Different
W
h
a
t
a
r
e
s
o
m
e
d
i
f
f
e
r
e
n
c
e
s
?
Why might they
be different?
fcc
bcc
fcc, 2 atoms
Remember we made several simplifications:
•
Interactions beyond nearest neighbors are
not included
•
Assumed harmonic potential
•
Ignored electron-phonon coupling
Real Phonon
Spectra Might
Look Slightly
Different
W
h
a
t
a
r
e
s
o
m
e
d
i
f
f
e
r
e
n
c
e
s
?
Why might they
be different?
fcc
bcc
fcc, 2 atoms
A and B are amplitudes of the motion of the two different atoms. The amplitudes need not be the same, but they could be.
The book actually makes the distance between same atoms a instead of my choice of 2a. Both are common. You will see shortly why I choose the axis this way. By doing this, I’m able to directly compare my result to the monatomic lattice as I make the masses more similar (next slide)
It’s also good for you to see it solved two different ways, so you can appreciate the subtle differences it makes in the solution.
The vibrational spectrum of structures with two atoms in a linear diatomic chain is examined, focusing on the equation of motion for atoms at even and odd positions, phonon dispersion, transverse acoustic and optical modes, longitudinal eigenmodes in 1D, and extending the 1D model to 3D for phonon dispersion. The discussion includes the unique labeling convention, different from monatomic structures, and the potential implications of opposite charged atoms in the optical mode.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
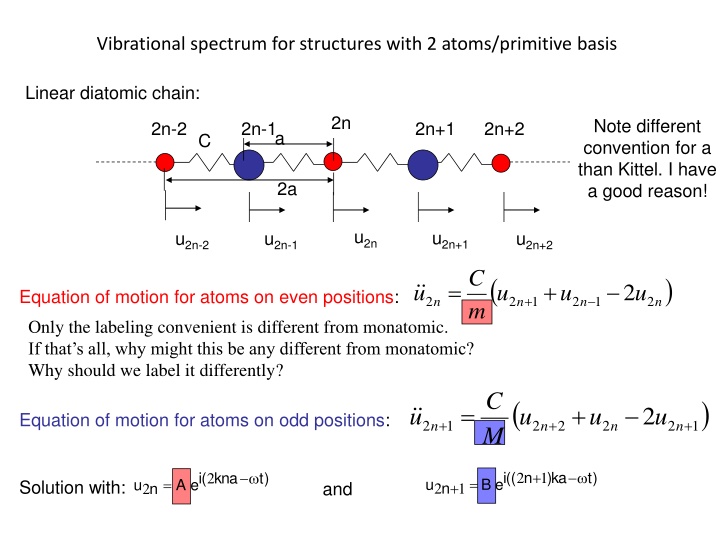
Vibrational spectrum for structures with 2 atoms/primitive basis Linear diatomic chain: 2n Note different convention for a than Kittel. I have a good reason! 2n-2 2n-1 2n+1 2n+2 a C 2a u2n u2n+1 u2n-2 u2n-1 u2n+2 C ( ) = + 2 u u u u Equation of motion for atoms on even positions: + 2 2 1 2 1 2 n n n n m Only the labeling convenient is different from monatomic. If that s all, why might this be any different from monatomic? Why should we label it differently? C ( ) = + 2 u u u u Equation of motion for atoms on odd positions: + + + 2 1 2 2 2 2 1 n n n n M + (( ie n ka ) 1 ) t ( ie kna 2 ) t 2 = = u B u A Solution with: and + n n 2 1 2
cos C C B ka C C C = 2 A 2= = + 2 ika ika 2 2 cos A B ka ( ) 2 A B e e A m m m m 2 2 m C C 2= C 2 2 cos B A ka = + 2 ika ika ( ) 2 B A e e B What happens? M M M C 1 1 = 2 = + 2 C m m M 2 C C C Phononendispersion = 2 2 2 2 2 4 cos ka m M Mm C = 2 2 2 C C C C Show video M + = 2 2 4 2 4 2 2 4 cos ka Mm M m Mm ( 1 u ) 0 = 2 C C C C 2 ( ) = m + + n 2 4 2 2 4 1 cos n ka u 2 M + Mm 2 u u m n + 2 2 1 n 2 2 sin2 ( ie kna 2 ) t ka = u A n 2 2 1 1 1 1 = k : 2 2=C = + C D D a 2 m M m M C ( 4 ) 2 2 + n 1 u 1 2 + 1 1 u sin ka = + 2 u C u = M + 2 1 2 + (( ie n ka ) 1 ) t C 2 + + 2 1 2 2 = n n n u B + C n 2 1 C , m M m M Mm = = 2 2 M m
Technically longitudinal only in 1D Transverse acoustic mode for diatomic chain A/B=1 + (( ie n ka ) 1 ) t 2 ( ie kna 2 ) t = u B = u A + n 2 1 n 2
Transverse optical mode for diatomic chain Technically longitudinal only in 1D Amplitudes of different atoms A/B=-m/M Transverse acoustic mode for diatomic chain A/B=1 + (( ie n ka ) 1 ) t 2 ( ie kna 2 ) t = u B = u A + n 2 1 n 2
Longitudinal Eigenmodes in 1D What if the atoms were opposite charged? Optical Mode: These atoms, if oppositely charged, would form an oscillating dipole which would couple to optical fields with ~a
Phonon Dispersion in 3D 1D model The 1D model can be extended to 3D if the variables u refer not to displacements of atoms but planes of atoms. 3D model
Phonon Dispersion in 3D 1D model The 1D model can be extended to 3D if the variables u refer not to displacements of atoms but planes of atoms. Need to include motions that are perpendicular to the wave vector. 3D model
Phonon Dispersion in 3D 1D model The 1D model can be extended to 3D if the variables u refer not to displacements of atoms but planes of atoms. Need to include motions that are perpendicular to the wave vector. These are called transverse acoustic modes (TA), as opposed to longitudinal acoustic modes (LA). 3D model
3D Dispersion curves Every 3D crystal has 3 acoustic branches, 1 longitudinal and 2 transverse Are the branches degenerate? LA Primary wave = faster wave TA Secondary wave = slower wave No, the perpendicular displacements will have different force ( spring ) constants from the longitudinal force constants. Example: Earthquake waves
Would you expect the two transverse branches to be degenerate? Think about a tetragonal lattice to debate this.
Number and Type of Branches Every crystal has 3 acoustic branches, 1 longitudinal and 2 transverse Every additional atom in the primitive basis contributes 3 further optical branches (again 2 transverse and 1 longitudinal) Sometimes transverse will be degenerate How would you know which branch is longitudinal? p atoms/primitive unit cell ( primitive basis of p atoms): 3 acoustic branches + 3(p-1) optical branches = 3p branches 1LA +2TA (p-1)LO +2(p-1)TO How many branches and of what type for a perovskite ABO3?
Write down the equation(s) of motion and guess solution 2D Square Lattice
.. u = + + + ( 2 ) ( 2 ) M C u u u C u u u lm , 1 + , 1 + , 1 , 1 l m l m lm l m l m lm ( ) C u u Write down the equation(s) of motion and guess solution + , 1 l m lm Ul,m+1 l,m+1 ( ) C u u ( ) C u u How would you add in second nearest neighbor interactions? , 1 l m lm , 1 + l m lm + ( ) i lk a mk a t = u u e x y Ulm lm Ul l- -1,m Ul+1,m l+1,m How will relate to u? lm o 1,m ( ) C u u + , 1 l m lm Ul,m 2D Square Lattice l,m- -1 1
.. u = + + + ( 2 ) ( 2 ) M C u u u C u u u lm , 1 + , 1 + , 1 , 1 l m l m lm l m l m lm ?2=2? Ul,m+1 l,m+1 ?(2 cos??? cos???) K Compare to 1D solution: ?2=2? 1 cos ?? ? Ulm lm Ul l- -1,m Ul+1,m l+1,m 1,m Ul,m l,m- -1 1 + ( ) i lk a mk a t = 2D Lattice u u e x y lm o
.. u = + + + ( 2 ) ( 2 ) M C u u u C u u u lm , 1 + , 1 + , 1 , 1 l m l m lm l m l m lm ?2=2? Ul,m+1 l,m+1 ?(2 cos??? cos???) K Compare to 1D solution: ?2=2? 1 cos ?? ? Ulm lm Ul l- -1,m Ul+1,m l+1,m How do you think you might change this if a rectangular lattice? 1,m Ul,m l,m- -1 1 + ( ) i lk a mk a t = 2D Lattice u u e x y lm o
.. u = + + + ( 2 ) ( 2 ) M C u u u C u u u lm , 1 + , 1 + , 1 , 1 l m l m lm l m l m lm ?2=2? Ul,m+1 l,m+1 ?(2 cos??? cos???) K Plot w vs k for the [10] and [11] directions. Ulm lm Ul l- -1,m Ul+1,m l+1,m 1,m Identify the values of at k=0 and at the BZ edges. (Hint: draw the BZ first) Ul,m l,m- -1 1 2D Lattice
.. u = + + + ( 2 ) ( 2 ) M C u u u C u u u lm , 1 + , 1 + , 1 , 1 l m l m lm l m l m lm ?2=2? ?(2 cos??? cos???) K Plot w vs k for the [10] and [11] directions. Ulm lm Ul l- -1,m Ul+1,m l+1,m 1,m Identify the values of at k=0 and at the BZ edges. (Hint: draw the BZ first) Ul,m l,m- -1 1 2D Lattice
?2=2? ?(2 cos??? cos???) K Plot w vs k for the [10] and [11] directions. Ulm lm Ul l- -1,m Ul+1,m l+1,m 1,m Identify the values of at k=0 and at the BZ edges. (Hint: draw the BZ first) Ul,m l,m- -1 1
Real Phonon Spectra Might Look Slightly Different What are some differences? Why might they be different? fcc bcc fcc, 2 atoms
Real Phonon Spectra Might Look Slightly Different What are some differences? Why might they be different? fcc bcc fcc, 2 atoms Remember we made several simplifications: Interactions beyond nearest neighbors are not included Assumed harmonic potential Ignored electron-phonon coupling
