Vectors: Magnitude, Direction, and Vector Addition
Vectors in physics are essential for understanding magnitude, direction, and addition. Explore concepts like scalars, Cartesian coordinates, and graphical methods for adding vectors graphically and mathematically. The properties of vector addition, including commutative and associative laws, are vital to solving physics problems involving motion and forces.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Chapter 3: Vectors Reading assignment: Chapter 3 Homework 3.1 (due Thursday, Sept. 13): CQ3, CQ4, 7, 11, 13, 20 Homework 3.2 (due Tuesday, Sept. 18): 19, 24, 29, 32, 36, 43, 48, AE1, AE4, AE5 CQ Conceptual question, AF active figure, AE active example No need to turn in paper homework for problems that mention it. In this chapter we will learn about vectors. properties, addition, components of vectors When you see a vector, think components! Multiplication of vectors will come in later chapters. Vectors have magnitude and direction.
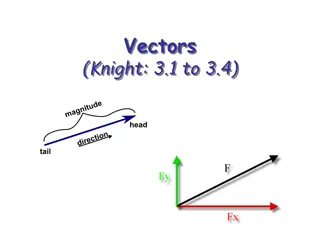
Vectors: Magnitude and direction Scalars: Only Magnitude A scalar quantity has a single value with an appropriate unit and has no direction. Examples for each: Vectors: Scalars: Motion of a particle from A to B along an arbitrary path (dotted line). Displacement is a vector
Coordinate systems Cartesian coordinates: ordinate abscissa
Vectors: Represented by arrows (example: displacement). Tip points away from the starting point. Length of the arrow represents the magnitude. In text: a vector is often represented in bold face (A) or by an arrow over the letter; . A A In text: Magnitude is written as A or . This four vectors are all equal because they have the same magnitude (length) and the same direction.
Adding vectors: Graphical method (triangle method): Example on blackboard: Draw vector A. Draw vector B starting at the tip of vector A. The resultant vector R = A + B is drawn from the tail of A to the tip of B.
Adding several vectors together. Resultant vector = + B C + + R A D is drawn from the tail of the first vector to the tip of the last vector. Example on blackboard:
Commutative Law of vector addition Example on blackboard: Order does not matter for additions + = + A B B A (Parallelogram rule of addition)
Associative Law of vector addition Example on blackboard: + B C + = + + ( ) ( ) A A B C The order in which vectors are added together does not matter.
Negative of a vector. The vectors A and A have the same magnitude but opposite directions. + = ( ) 0 A A A -A
Subtracting vectors: A B = + ( ) A B Example on blackboard:
Multiplying a vector by a scalar The product mA is a vector that has the same direction as A and magnitude mA (same direction, m times longer). The product mA is a vector that has the opposite direction of A and magnitude mA. Examples: 5 A 1 3 B
Components of a vector Example on blackboard: The x- and y-components of a vector: = cos A A x = sin A A y The magnitude (length) of a vector: 2 2 = + A = A A A x y A y = 1 tan The angle between vector and x-axis: A x
i-clicker: You walk diagonally from one corner of a room with sides of 4 m and 3 m to the other corner. What is the magnitude of your displacement (length of the vector )? A A. 3 m B. 4 m C. 5 m D. 7 m E. 12 m A What is the angle
The signs of the components Ax and Ay depend on the angle and they can be positive or negative. (Examples)
Unit vectors A unit vector is a dimensionless vector having a magnitude of 1. Unit vectors are used to indicate a direction. i, j, k represent unit vectors along the x-, y- and z- direction i, j, k form a right-handed coordinate system Right-handed coordinate system: Use your right hand: x thumb x index y index finger or: y middle finger z middle finger z thumb
i-clicker: Which of the following coordinate systems is not a right-handed coordinate system? A B C z x y y z y x x z
The unit vector notation for the vector A is: A = Axi + Ayj The column notation often used in this class: = A A x A y
Vector addition using unit vectors: Only add components!!!!! R = A + B We want to calculate: R = (Ax + Bx)i + (Ay + By)j From diagram: Rx = Ax+ Bx Ry = Ay+ By The components of R:
Vector addition using unit vectors: The magnitude of a R: 2 2 = + = + + + 2 2 ( ) ( ) R R R A B A B x y x x y y + + R R A A B B y y y = = tan The angle between vector R and x-axis: R x x x
Blackboard example 3.1 A commuter airplane takes the route shown in the figure. First, it flies from the origin to city A, located 175 km in a direction 30 north of east. Next, it flies 153 km 20 west of north to city B. Finally, it flies 195 km due west to city C (a) Find the location of city C relative to the origin (the x- and y- components, magnitude and direction (angle) of R. (b) The pilot is heading straight back to the origin. What are the coordinates of this vector.
Polar Coordinates A point in a plane: Instead of x and y coordinates a point in a plane can be represented by its polar coordinates r and = cos x r y = = + 2 2 tan r x y = sin y r x
Blackboard example 3.2 3 3 = A vector and a vector are given in 4 = A B 2 Cartesian coordinates. = 3 + . B 4 C A (a) Calculate the components of vector C (b) What is the magnitude of ? C (c) Find the polar coordinates of .