Exploring Vectors: Magnitude, Direction, and Operations
Delve into the world of vectors, understanding their properties, how to add and subtract them, and determining their components in different coordinate systems. Learn about scalar quantities, vector quantities, the tip-to-tail rule, and the role of unit vectors in calculations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
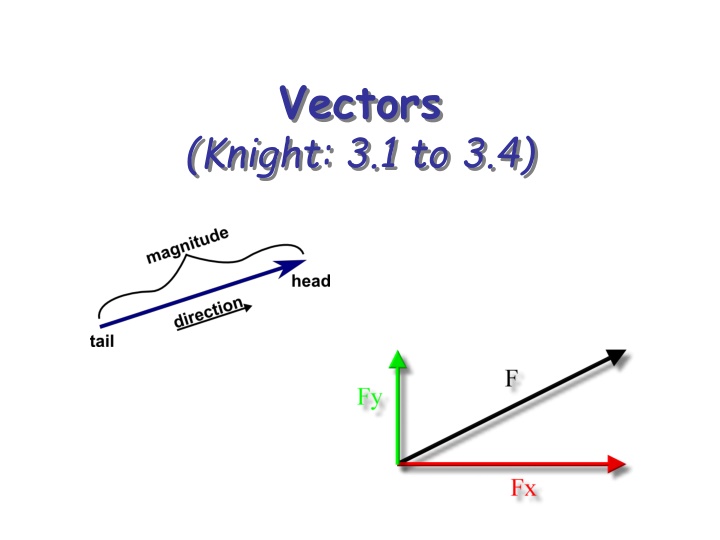
Vectors (Knight: 3.1 to 3.4)
Scalars and Vectors Temperature = Scalar Quantity is specified by a single number giving its magnitude. Velocity = Vector Quantity is specified by three numbers that give its magnitude and direction (or its components in three perpendicular directions).
Properties of Vectors Two vectors are equal if they have the same magnitude and direction.
Clicker Question 1 Question: Which vector shows the sum of A1 + A2 + A3 ?
Coordinate Systems and Vector Components Determining the Components of a Vector 1. The absolute value |Ax| of the x-component Ax is the magnitude of the component vector . 2. The sign of Axis positive if points in the positive x-direction, negative if points in the negative x-direction. 3. The y- and z-components, Ay and Az, are determined similarly. xA x A x A Knight s Terminology: The x-component Ax is a scalar. The component vector is a vector that always points along the x axis. x A The vector is , and it can point in any direction. A
Cartesian and Polar Coordinate Representations
Unit Vectors i = = = = (1,0,0) unit vector in +x-direction = "i-hat" j (0,1,0) unit vector in +x-direction = "j-hat" = = (0,0,1) unit vector in +z-direction = "k-hat" k = + + = + + = ( , , ) A A A A A i A j A k A A A x y k x y z x y z Example: i j = + = (4, 2,5) 4 2 5 B k
Working with Vectors ^ A = 100 i m B = ( 200 Cos 450 i + 200 Cos 450 j ) m = ( 141 i + 141 j ) m ^ ^ ^ ^ C = A + B = (100 i m) + (-141 i + 141 j ) m = (-41 i + 141 j ) m ^ ^ ^ ^ C = [Cx2 + Cy2] = [(-41 m)2 + (141 m)2] = 147 m = Tan-1[Cy/|Cx|] = Tan-1[141/41] = 740 Note: Tan-1 ATan = arc-tangent = the angle whose tangent is
Tilted Axes Cx = C Cos Cy = C Sin