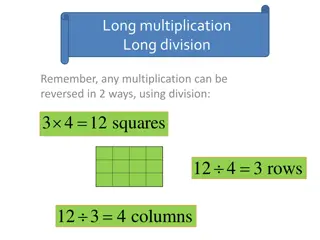
Vector Multiplication
Learn about vector multiplication, unit vectors, magnitude calculations, scalar dot products, cross products, and angle determinations between vectors. Explore video explanations and visual representations for a comprehensive understanding of vector mathematics concepts.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Vector Multiplication Return to Table of Contents https://njctl.org/video/?v=byuPJNfJT1U
Unit Vectors Unit vectors describe directions in space. They do not represent any physical quantity and have a magnitude of 1. indicates the x direction indicates the y direction indicates the z direction Any given Vector can be presented in terms of unit vectors:
Unit Vectors When two vectors A and B are represented by their components in the xyz plane using unit vectors, the resultant vector R = A + B is expressed as: The magnitude of R is: Pythagoras in 3D!
13 What is the magnitude of the sum of the following vectors? A B C D E 9.3 12.3 5.1 10.7 3 C Answer https://njctl.org/video/?v=N0jzk3Wi3Xc
15 What is the closest value for the scalar dot product of vectors A and C ? A B C D E 0 14 42 -14 -42 4 Answer 7 D 6 65o 45o https://njctl.org/video/?v=VspBDduAT44
Vector Cross Product The vector cross product yields a vector quantity and its magnitude is defined as: The cross product can be viewed as the "projection" of the magnitude of A on a line perpendicular to vector B(Asin ), multiplied by the magnitude of B. The magnitude of this product can be positive or zero depending on angle . ranges from 0 to 1800. The vector cross product is a minimum when the two vectors are in line, = 00. It is a maximum when = 900. https://njctl.org/video/?v=N1WKTxZt_xE
Vector Cross Product The vector cross product yields a vector quantity and its magnitude is defined as: Since the cross product results in a vector, it must also have a direction. In previous physics courses, the concept of the "right hand rule" was developed to give this direction. Physicists don't use the right hand rule to solve complex problems - they use the vector cross product.
19 Solve for the angle between vectors and Answer 98o 278o 57o 85o 124o A B C D E A https://njctl.org/video/?v=ak5u5eVQHzs
20 Two vectors are given: The angle between vectors A and B, in degrees, is: Answer o A B C D E 117 o 76 150 o o 29 161 B o https://njctl.org/video/?v=BkKKnh__U9c
21 Two vectors are given: Solve for the magnitude of Answer 33 29 25 21 17 A B C D E A See next slide for worked out solution. https://njctl.org/video/?v=-oJOuHBjJTs
Two vectors are given: Worked Out Solution Solve for the magnitude of
