Understanding Volume Formulas for Geometric Shapes
Exploring the concepts of volume calculation for various geometric shapes like cylinders, prisms, cones, and pyramids. Learn about the formulas, properties, and relationships between different parts of these shapes. Visual aids and step-by-step explanations provided for better understanding.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
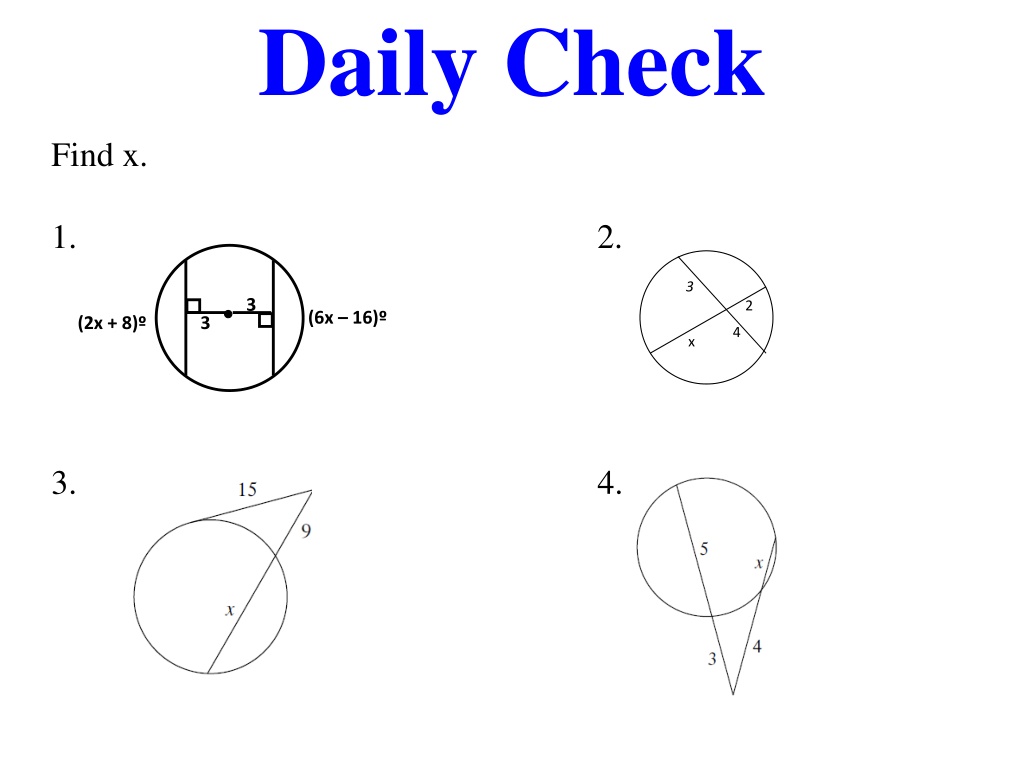
Daily Check Find x. 1. 2. 3 3 2 (6x 16) (2x + 8) 3 4 x 3. 4.
CCGPS Geometry UNIT QUESTION: What special properties are found with the parts of a circle? Standard: MMC9-12.G.C.1-5,G.GMD.1-3 Today s Question: How do we find the volume of cylinders, prisms, cones, and pyramids? Standard: MMC9-12.G.GMD1 and 3
VOLUME has cubic units Cm3, ft3, units3 VOLUME = the number of cubic units contained in its interior
Volume = lengthwidthheight In a CUBE they are all the same The volume of a cube is side3 Volume = s3 Volume = 43 Volume = 64 ft3 4 ft
When a prism is NOT a cube B(area of the BASE) The formula for B will depend on the shape of the base.
Volume Formula for Prisms & Cylinders V = Bh
Volume of a Prism V = Bh B = area of the BASE h = HEIGHT V = area of the Base h 4 in 3 in 5 . = base 5 . = of 3 height 4 of 2 2 V V 2 in V = 12 in3
Volume of a Cylinder V = Round to the nearest tenth. Bh = = 2 V V r h 7 cm 72 5 5 cm V = 769.7 cm3
How many cones will it take to fill the cylinder? They have the same size base. They also have the same height.
Volume Formula for Cones & Pyramids 1 3 = V Bh
1 3 Find the volume. = V Bh 8 ft (12 10 8) = V 3 = 320 ft 3 V 10 ft 12 ft
What is the volume of this cone? Round to the nearest tenth. 1 3 = V Bh 2 ( r 3 ) h = V 3 cm 2 ( 2 3 3 ) 2 cm = V = 12.6 cm 3 V
2 Types of Answers Exact Pi will be in your answer Rounded Type the Pi button on your calculator Toggle your answer Do NOT write Pi in your answer
If you cut a sphere right down the middle you would create two congruent halves called HEMISPHERES. You can think of the globe. The equator cuts the earth into the northern and southern hemisphere.
Look at the cross section formed when you cut a sphere in half. What shape is it? A circle!!! This is called the GREAT CIRCLE of the sphere.
Surface Area of a Sphere = 2 4 SA r
Surface Area of a Sphere SA=4 r2 SA=4 82 (round to the nearest hundredths) 8 in SA 804.25 in2
Surface Area of a Sphere SA=4 r2 SA=4 52 (round to the nearest hundredths) 10 cm SA 31416 cm2 .
The circumference of a great circle of a sphere is 25 inches. Find the surface area of the sphere. (Round to the nearest tenths.) 25 2 = r 25 2 12.5 r = = 2 12.5 in 25 in SA 4 = 2 SA 198.9 =
A sphere is inscribed in a cube of volume 27 cubic meters. What is the surface area of the sphere? Give an exact answer and an answer rounded to the nearest hundredth. SA=4 r2 SA ( ) 2 4 1.5 = 2 2 SA 9 m = 28.27m
Volume of a Sphere 4 3 = 3 V r
Volume of a Sphere (round to the nearest hundredths) 4 3 = 3 V r 2 cm = 4 3 3 2 V 3 V 33.51 cm =
Volume of a Sphere (round to the nearest hundredths) 4 3 = 3 V r 10 cm = 4 3 3 5 V 3 V 523.60 cm =
Volume of a Sphere A sphere is inside a cube. The cube has a volume of 27 cm3. Find volume of the sphere. Round to the nearest hundredths. 4 1.5 3 14.14 m V = ( ) 3 v = 3 c