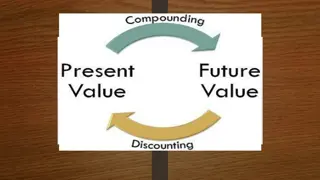
Understanding the Importance of Time Value of Money
Explore the significance of time value of money in financial decisions through topics like interest rates, types of interest, compound interest, future values, and comparing simple versus compound interest. Learn how time allows for earning interest, postponing consumption, and increasing the value of investments over time.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
TIME VALUE OF MONEY R.A. EF KA ONAT A
The Interest Rate The Interest Rate Which would you prefer -- $10,000 today or $10,000 in 5 years? Obviously, $10,000 today. You already recognize that there is TIME VALUE TO MONEY!!
Why TIME? Why TIME? Why is TIME such an important element in your decision? TIME allows you the opportunity to postpone consumption and earn INTEREST.
INTEREST INTEREST Interest is the difference between Future Value and Present Value. Interest isthe PRICE of the MONEY
Interest Rate Interest Rate What I put, What I got! r= I/ PV
Types of Interest Types of Interest Simple Interest Interest earned only on the original investment; no interest is earned on interest. Compound Interest Interest earned on any previous interest earned, as well as on the principal borrowed (lent).
The greatest mathematical discovery of all time is compound interest. Albert Einstein 7
Why Compound Interest? Why Compound Interest? Future Value of a Single $1,000 Deposit 20000 Future Value (U.S. Dollars) 10% Simple Interest 7% Compound Interest 10% Compound Interest 15000 10000 5000 0 1st Year 10th 20th Year 30th Year Year
Future Values Future Value: Amount to which an investment will grow after earning interest. Let r = annual interest rate Let t = time (years) Simple Interest Compound Interest r t + FV = Initial investment (1 ) + )t FV = Initial investment (1 r Simple Compound
Compare the interest earned from an investment 125 TL for 10 years at 12% simple interest with that earned by the same amount for 10 years at 12 % compounded annually? Simple interest Compound interest r t + + FV = Initial investment (1 ) )t FV = Initial investment (1 r Simple Compound = 125*(1+12%*10) =275 =125*(1+12%)^10 =388 275-125=150 388-125=263 Interest on interest: 263-150= 113
INTEREST SYSTEM INTEREST SYSTEM Present Value or Rate (r) Principal (P or PV) Annuities (A) PMT Periods (t) NPER Future Value (FV) Interest: The PRICE of the MONEY
How long would it take for an investor to double his Money at 10% interest per year, compounded annually? Ans: 7 years
What is the present value of a future payment 100 TL to be received 20 years from now, if the principle is invested at 8% per year, compounded annually? Ans: 21.45 TL
Annuities Annuity: a sequence of equal cash flows, occurring at the end of each period. This is known as an ordinary annuity. 0 PV 1 2 3 4 FV 14
Annuity-due A sequence of periodic cash flows occurring at the beginning of each period. 0 1 2 3 4 PV FV 15
What is the difference between an ordinary annuity and an annuity due? Ordinary Annuity 0 1 2 3 i% PMT PMT PMT Annuity Due 0 1 2 3 i% PMT PMT PMT 16
Example of an Example of an Ordinary Annuity Ordinary Annuity -- -- FVA FVA Cash flows occur at the end of the period 0 1 2 3 4 7% $1,000 $1,000 $1,000 $1,070 $1,145 FVA3= $1,000(1.07)2 + $1,000(1.07)1 + $1,000(1.07)0 $3,215 = FVA3 = $1,145 + $1,070 + $1,000 = $3,215
Examples of Annuities Examples of Annuities Student Loan Payments Car Loan Payments Insurance Premiums Mortgage Payments Retirement Savings
Example of an Example of an Ordinary Annuity Ordinary Annuity -- -- PVA PVA Cash flows occur at the end of the period 0 1 2 3 4 7% $1,000 $1,000 $1,000 $934.58 $873.44 $816.30 $1,000/(1.07)1 + $1,000/(1.07)2 + $1,000/(1.07)3 = $934.58 + $873.44 + $816.30 = $2,624.32 PVA3= $2,624.32 = PVA3
Piece Piece- -At At- -A A- -Time Time 0 1 2 3 4 5 10% $600 $600 $400 $400 $100 $545.45 $495.87 $300.53 $273.21 $ 62.09 $1677.15 = PV0of the Mixed Flow
Impact of Frequency Impact of Frequency Julie Miller has $1,000 to invest for 2 Years at an annual interest rate of 12%. Annual FV2 = 1,000(1+ [.12/1])(1)(2) = 1,254.40 Semi FV2= 1,000(1+ [.12/2])(2)(2) = 1,262.48
Impact of Frequency Impact of Frequency FV2= 1,000(1+ [.12/4])(4)(2) Qrtly 1,266.77 Monthly FV2 = = 1,000(1+ [.12/12])(12)(2) = 1,269.73 FV2= 1,000(1+[.12/365])(365)(2) = 1,271.20 Daily
Which is more desirable 10% compounded monthly than 10% compounded yearly?
Effective Annual Effective Annual Interest Rate Interest Rate Effective Annual Interest Rate The actual rate of interest earned (paid) after adjusting the nominal rate for factors such as the number of compounding periods per year. (1 + [ i / m ] )m- 1
Effective Annual Interest Rate Effective Annual Interest Rate Basket Wonders (BW) has a $1,000 CD at the bank. The interest rate is 6% compounded quarterly for 1 year. What is the Effective Annual Interest Rate (EAR)? = ( 1 + 6% / 4 )4- 1 = 1.0614 - 1 = .0614 or 6.14%! EAR
If you take out an 24.000 TL car loan that callls for 48 monthly payments starting after 1 month at an APR of 12%, A) What is your monthly payment? B) What is the effective annual interest rate on the loan? Answer A: PMT (0.12/12; 48; 24.000) Answer B: EFFECTIVE (0.12; 12)
PRACTISES PRACTISES 1.You will require 700 TL in 5 years. If you earn 5% interest on your funds, how much will you need to invest today in order to reach your savings goal? Ans: 548.47
2. What is the present value of the following cash- flow stream if the interest rate is 6% Year 1 2 3 Casf Flow 200 400 300 Ans: 796.54
3. How long will it take for 400 TL to grow to 1000 TL at the interest rate specified? A. 4% B. 8% C. 16% Answer: A: 23,36
4. Find the effective annual interest rate for each case APR COMPOUNDING PERIOD 1 Month 3 Month 6 Month 12% 8% 10%
5. A famous quarterback just signed a 15 milllion contract providing 3 million a year. A less famous receiver signed a 14 milion 5 year contract providing 4 million now and 2 million a year for 5 years. Who is better paid? (The interest rate is 10%)
6. If you take out an 8000 car loan that calls for 48 monthly payments of 240 each, what is the APR of the loan ? What is the effective annual interest rate on the loan?
7. Your landscaping company can lease a truck for 8000 a year (paid at year-end) for 6 years. It can instead buy the truck for 40000. The truck will be valueless after 6 years. It can instead buy the truck for 40000 . If the interest rate your company can earn on its funds is 7%, is it cheaper to buy or lease?
8. I now have 20000 in the bank earning interest of 0.5% per month. I need 30000 to make a down payment on a house. I can save an additional 100 per month. How long will it take me to accumulate the 30000?
9. You invest 1000 today and expect to sell your investment for 2000 in 10 years. a) Is this a good deal if the discount rate is 6%? b) What if the discount rate is 10%?
10. You believe you will need to have saved 500.000 by the time you retire 40 years in order to live comfortably. If the interest rate is 6% per year, how much must you save year to meet you retirement goal?
11) You believe you will spend 40.000 a year for 20 years once you retire in 40 years. If the interest rate 6% per year, how much must you save each year until retirement to meet your retirement goal?
12. Your wealthy uncle established a 1000 bank account for you when you born. For the first 8 years of your life, the interest rate earned on the account was 6%. Since then, rates have been only 4%. Now you are 21 years old and ready to cash in. How much is in your account?
13. Suppose that 100 TL is deposited in the bank each year. How long will it take to accumulate 2.101, 60 TL if the interest rate 6% per year, compounded annually? Ans. 14 years
Net Present Value as an Investment Criteria Year Project A Project B 0 1 - 200 80 - 200 100 2 80 100 3 80 100 4 80 a. If the opportunity cost of capital is 11%, which of these projects is worth pursuing? b. Which project would you choose if the opportunity cost of capital were 16%?
15. Calculate the net present value of the following project for discount rates 0%, 50% and 100% . C0 - 6.750 C1 4.500 C2 18.000