Understanding Rotational Motion and Angular Variables in Physics
Exploring rotational motion in physics, including the definition of angles in radians, conversion between degrees and radians, angular variables, torque, Newton's second law for rotating bodies, moment of inertia, rotational kinetic energy, and angular momentum. Learn about key concepts and equations related to rotational motion and how they apply in various scenarios like ice-skating stunts and rolling cylinders.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
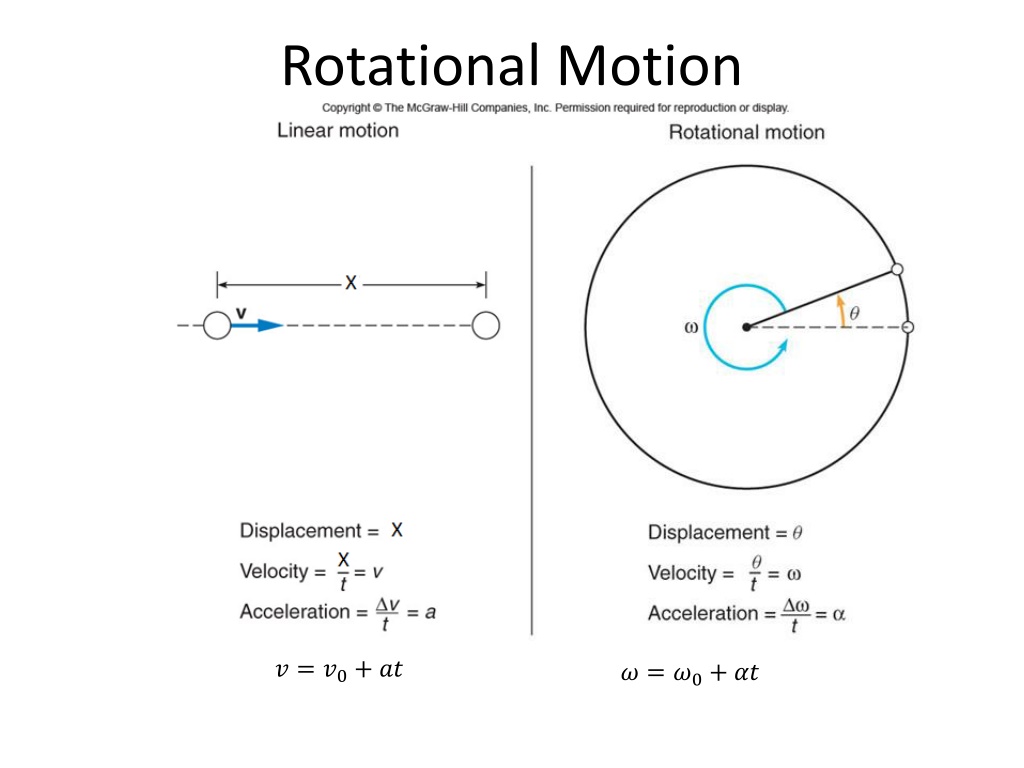
Rotational Motion ? = ?0+ ?? ? = ?0+ ??
The angle In radian measure, the angle is defined to be the arc length s divided by the radius r.
Conversion between degree and radian rad = 1800
Angular Variables and Tangential/Linear Variables In the ice-skating stunt known as crack- the-whip, a number of skaters attempt to maintain a straight line as they skate around one person (the pivot) who remains in place. ? =? ? = ?? ? ? ?= ?? ? ? = ?? ? ?= ?? ? ? = ??
Torque, Torque depends on the applied force and lever-arm. Torque = Force x lever-arm Torque is a vector. It comes in clockwise and counter-clock wise directions. Unit of torque = N m
Newtons 2nd law and Rotational Inertia ? = ?? ?? = ??? ?? = ???? ?? = ??2? ? = ?? ? = ??2 I = Rotational Inertia or Moment of inertia.
NEWTONS SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS
Moment of Inertia of point masses ? = ?1?12+ ?2?2 2+ Moment of inertia (or Rotational inertia) is a scalar. SI unit for I: kg.m2
Moment of Inertia, I for Extended regular- shaped objects
ROTATIONAL KINETIC ENERGY
Angular Momentum The angular momentum L of a body rotating about a fixed axis is the product of the body's moment of inertia I and its angular velocity with respect to that axis: Angular momentum is a vector. SI Unit of Angular Momentum: kg m2/s.
Conservation of Angular Momentum
Angular momentum and Bicycles Explain the role of angular momentum in riding a bicycle?
Equations Sheet MOTION Linear t d; (d = r ) v = d/t; (v = r ) = /t a = v/t; (a = r ) v = v0 + at v2 = v02 + 2ad d = v0t + at2 d = (v + v0)t force = F Mass =m Rotational t Time interval Displacement Velocity Acceleration = /t = 0+ t 2= 02+ 2 = 0t + t2 = ( + 0)t torque = Rotational inertia = I = miri2 net= I L= I Ii i= If f Kinematic equations To create Inertia Newton s 2nd Law Momentum Conservation of momentum Fnet = ma p = m V mivi = mfvf Kinetic Energy Translational Kinetic Energy = TKE = mv2 W=F d Rotational Kinetic Energy = RKE = I 2 W= Work