Understanding Pyramids and Prisms in Geometry
Explore the common characteristics of pyramids and prisms, learn about their definitions, faces, edges, and vertices, and understand Euler's formula for polyhedra. Discover the properties of different pyramids and prisms and predict results based on various base shapes. Verify Euler's formula for prisms and delve into the fascinating world of geometrical solids.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
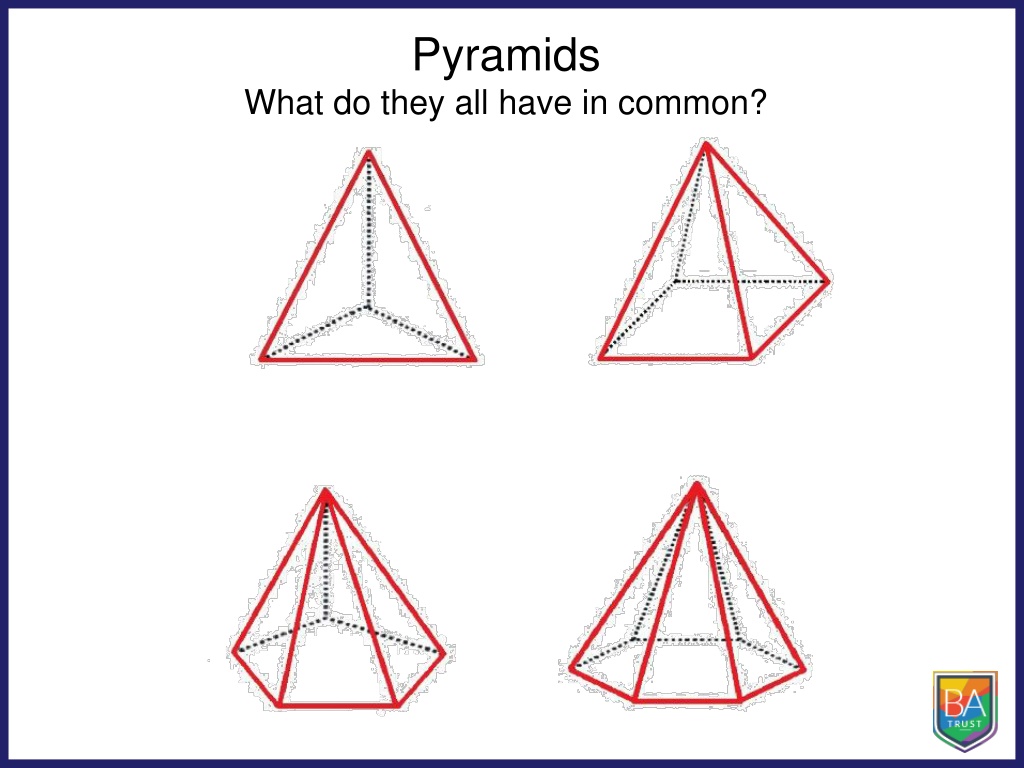
Pyramids What do they all have in common?
Pyramids Definition A solid object where: The base is a polygon (a straight- sided flat shape) The sides are triangles which meet at the top (the apex).
Prisms What do they all have in common?
Prisms Definition A solid object with two identical ends and flat sides: The sides are rectangles (or parallelograms) The cross section is the same all along its length The shape of the ends give the prism a name, such as "triangular prism"
Pyramids Fill in the table for each of the pyramids Solid Number of Faces Number of Edges Number of Vertices Can you find a predict the results for a heptagonal or octagonal based pyramid? What about an n-agonal based pyramid?
Pyramids Fill in the table for each of the pyramids Solid Number of Faces Number of Edges Number of Vertices Can you find a connection between the Faces, Edges and Vertices?
Eulers Formula for Polyhedra V + F - E = 2. The formula was discovered by and bears the name of the famous Swiss mathematician Leonhard Euler (1707 - 1783) It is true for all polyhedra. (singular polyhedron)
Prisms Fill in the table for each of the prisms Solid Number of Faces Number of Edges Number of Vertices Can you find a predict the results for a heptagonal or octagonal prism? What about an n-agonal prism?
Prisms Fill in the table for each of the prisms Solid Number of Faces Number of Edges Number of Vertices Verify that Euler s formula also works for the prisms in this table
Other Polyhedra Fill in the table for each of these platonic solids Solid Number of Faces Number of Edges Number of Vertices Octahedron Dodecahedron Icosahedron How can you use Euler s formula to fill in this table?