Understanding Platonic Solids: Shapes of Harmony and Elements
Explore the fascinating world of Platonic solids, 3D shapes with faces made of regular polygons, each representing a different element. Dive into the history, symbolism, and unique characteristics of the tetrahedron, cube, octahedron, and dodecahedron through their elemental associations. Discover the profound geometric relationships that define these sacred shapes and their significance in various philosophies and disciplines.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
PLATONIC SOLIDS BY: PRABHNOOR KAUR AND OLIVIA COHEN
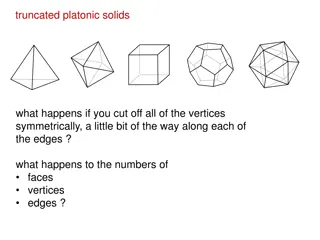
WHAT IS A PLATONIC SOLID? A 3-D solid figure with faces made of the same regular polygon This 3-D shape is created because of the interior angle sum at a vertex in each platonic sold the interior angle of certain polygons multiplied by the number of faces at each vertex is less than 360 degrees creating a 3D structure. In a platonic solid, the angles sum of all vertices has to be less than 360 degrees which is why only a tetrahedron, cube, octahedron, dodecahedron, icosahedron are the only platonic solids able to be formed because of the polygons they use for their faces. The relationship between the faces, edges and vertices of a platonic solid is F+V-2=E
THE HISTORY OF PLATONIC SOLIDS THE HISTORY OF PLATONIC SOLIDS Based off of the writings of Plato who was a Greek philosopher (430 B.C) he associated each of the solids with the five different atoms of the universe which were fire, air, water, earth, and cosmos (the universe). Plato associated the tetrahedron with fire, cube with the earth, octahedron with air, icosahedron with water, and the dodecahedron with cosmos
TETRAHEDRON Fire element: symbol of spiritual balance because of its flat sitting Regular polygon used: triangle There are 4 faces, 6 edges, and 4 vertices There are 3 faces and 3 edges at a vertex The interior angles at a vertex is 60 degrees -The sum of the interior angles at a vertex is 180 degrees
CUBE Earth element: symbol of connection and stability because it stands grounded Regular polygon used: the square There are 6 faces, 12 edges, and 8 vertices There are 3 faces at a vertex and 3 edges at a vertex The interior angles at a vertex is 90 degrees -The sum of the interior angles at a vertex is 270 degrees
OCTAHEDRON Air element: symbol of reflection in life because of its self- reflecting shape Regular polygon used: triangle There are 8 faces, 12 edges, and 6 vertices There are 4 faces and 4 edges at a vertex The interior angles at a vertex is 60 degrees -The sum of the interior angles at a vertex is 240 degrees
DODECAHEDRON Universe element: symbolized a higher connection with the universe Regular polygon used: pentagon There are 12 faces, 30 edges, and 20 vertices There are 3 faces and 3 edges at a vertex The interior angles at a vertex is 108 degrees -The sum of the interior angles at a vertex is 324 degrees
ICOSAHEDRON Water element: symbolized the importance of transformation and movement Regular polygon used: triangle There are 20 faces, 30 edges, and 12 vertices There are 5 faces and 5 edges at a vertex The interior angles at a vertex is 60 degrees -The sum of the interior angles at a vertex is 300 degrees
EACH PLATONIC SOLID HAS A DUAL Every platonic solid has a dual pair A dual pair has a pattern between the vertices and faces A platonic solid with the same number of vertices as another platonic solid s sides, fits into that platonic solid A platonic solid s dual pair can be made by putting a dot on each face of the platonic solid and then connecting them all Duals have the same amount of edges
PATTERN OF DUALS Platonic Solid # Faces # Edges # Vertices Tetrahedron 4 6 4 Cube 6 12 8 Octahedron 8 12 6 Dodecahedron 12 30 20 Icosahedron 20 30 12
IMAGES OF DUALS Icosahedron and Dodecahedron Octahedron and Cube Tetrahedron
BIBLIOGRAPHY https://www.asiact.org/archive/numerology/10sequence.asp http://www.latroika.com/mathoman/pix/ http://www.thingiverse.com/thing:693660 http://www.shlomifish.org/MathVentures/dodeca. gif https://encrypted- tbn3.gstatic.com/images?q=tbn:ANd9GcTGJujUE3 _wOlN2FpXuA1- 3v2FUnfzZCSJYonj7OIyyLXae8Sux http://nlvm.usu.edu/en/nav/frames_asid_131_g_4_t_3.html?o pen=instructions&from=category_g_4_t_3.html