Understanding Persistent Data Structures and Version Control
Exploring persistent data structures and version control concepts, including partial persistence, full confluence, purely functional approaches, and ephemeral versions. Delve into tree lists, full and partial persistence, query methods, retroactive updates, planar point location, path copying in trees, and version identification in a time-based system. Discover the intricacies of updating, merging, and querying across different versions to maintain data integrity and efficiency while managing evolving datasets.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
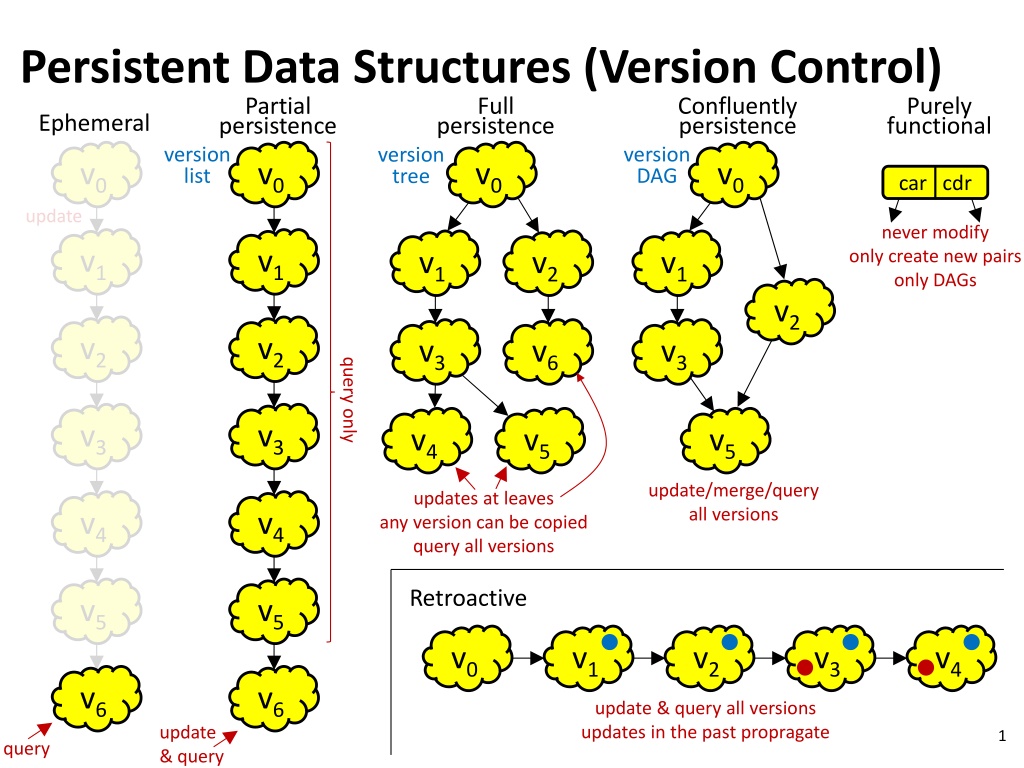
Persistent Data Structures (Version Control) Partial persistence persistence version tree list Full Confluently persistence version DAG Purely functional Ephemeral version v0 v0 v0 v0 car cdr update never modify only create new pairs only DAGs v1 v1 v1 v2 v1 v2 v2 v2 v3 v6 v3 query only v3 v3 v4 v5 v5 update/merge/query all versions updates at leaves any version can be copied query all versions v4 v4 Retroactive v5 v5 v0 v1 v2 v3 v4 v6 v6 update & query all versions updates in the past propragate update & query 1 query
Planar Point Location T1 T2 T3 T4 T5 T6 T7 Partial persistent search trees update O(n log n) preprocessing, O(log n) query 2
Path Copying (trees) root pointer c c a f f d e g 3
Partial Persistence Version ID = time = 0,1,2,... Fat node (any data structure) record all updates in node (version,value) pairs field updates O(1) field queries predecessor wrt version id (search tree/vEB) field1: field2: (0,x) (3,y) (7,z) (0,a) (14,c) (16,b) Node copying (O(1) degree data structures) Persistent node = collection of nodes, each valid for an interval of versions, with extra updates, = max indegree pointers must have subinterval of the node pointing to; otherwise copy and insert pointers (cascading copying) NB: Needs to keep track of back-pointers [0,8[ [8,13[ [13, [ field1: field2: (0,x) (3,y) field1: field2: (8,z) (10,w) field1: field2: (13,w) (15,y) (0,a) (7,c) (8,c) (9,d) (13,e) (14,c) 4
Full Persistence 1 4 3 2 increasing version 1 4 7 5 3 6 2 preorder traversal Version list 7 5 6 (order maintenance data structure) Version tree (numbers = version ids) Fat node Updates (1,x) (6,y) (7,z) to a field Queries = binary search among versions Update (7,z): Insert 7 as leftmost child of 4; insert pairs for 7 and 5=succ(7) Node splitting ( 2 ekstra fields) field: (1,x) (7,z) (5,x) (6,y) (2,x) [5,3[ [4,3[ [4,5[ [5, [ [0, [ [0,5[ split field1: (1,a) (4,b) field2: (1,f) (7,g) field1: (1,a) (4,b) (3,a) (2,c) field2: (1,f) (7,g) (5,f) field1: (5,b) (3,a) (2,c) field2: (5,f) 5 version 5
Persistence Techniques [N. Sarnak, R.E. Tarjan, Planar point location using persistent search trees, Communications of the ACM, 29(7), 669-679, 1986] Partial persistence, trees, O(1) access, amortized O(1) update [J.R. Driscoll, N. Sarnak, D.D. Sleator, R.E. Tarjan, Making Data Structures Persistent, Journal of Computer and System Sciences, 38(1), 86-124, 1989] Partial & full persistence, O(1) degree data structures, O(1) access, amortized O(1) update [P.F. Dietz, R. Raman, Persistence, Amortization and Randomization. Proceedings 2nd Annual ACM-SIAM Symposium on Discrete Algorithms, 78-88, 1991] [G.S. Brodal, Partially Persistent Data Structures of Bounded Degree with Constant Update Time,Nordic Journal of Computing, volume 3(3), pages 238-255, 1996] Partial persistence, O(1) degree data structures, O(1) access & updates update [P.F. Dietz, Fully Persistent Arrays. Proceedings 1st Workshop on Algorithms and Data Structures, LNCS 382, 67-74, 1989] Full persistence, RAM structures, O(loglog n) access, O(loglog n) amortized expected updates 6
Comparison of Persistence Techniques Copy data structure for each version no query overhead, slow updates & wastes a lot of space Record updates & keep current version fast updates & queries to current version, space efficient, slow queries in the past Path copying applies to trees, no query overhead, space overhead = depth of update Fat node partial persistence: O(1) updates and space optimal, loglog n query overhead full persistence: O(loglog n) expected amortized updates and space optimal, loglog n query overhead Node copying/splitting fast updates & queries (amortized updates for full persistence) only works for pointer-based structures with O(1) degree 7
Fractional Cascading Basic Idea : 2 x BinSearch(x) 1 BinSearch(x) + O(1) L1 L2 5 8 12 14 17 L1 2 5 8 11 21 25 27 31 33 42 L2 catalog graph 19 20 35 37 41 Build bridges (and pointers to nearest original element) Searches to next list : Traverse nearest bridge Construction : Repeatedly create bridges until all gaps O(1) O(1) nodes 18 2 5 8 11 14 20 21 25 27 31 33 41 42 bridges 5 8 12 14 17 19 20 27 35 37 41 Generalizes to catalog graphs of degree O(1) 8
Fractional Cascading Techniques [Bernard Chazelle, Leonidas J. Guibas, Fractional Cascading: I. A Data Structuring Technique, Algorithmica, 1(2): 133-162, 1986.] [Bernard Chazelle, Leonidas J. Guibas: Fractional Cascading: II. Applications. Algorithmica 1(2): 163-191 (1986)] Static fractional cascading, O(1) worst-case access [Kurt Mehlhorn, Stefan N her: Dynamic Fractional Cascading. Algorithmica 5(2): 215-241 (1990)] Dynamic fractional cascading, O(loglog N) worst-case access, amortized insert and delete Insertion or deletion only, O(1) per worst-case access, amortized insert or delete 9