Understanding Measurement Bounds and Accuracy
Exploring the concepts of significant figures, bounds, accuracy, and ranges in measurement. From determining the smallest and largest possible lengths to finding lower and upper bounds based on accuracy, this content focuses on practical exercises and explanations to enhance understanding. Learn how to represent ranges on a number line and easily calculate bounds with simple methods. Dive into scenarios involving concert capacities, insect lengths, runner speeds, and cube dimensions, all aimed at improving measurement comprehension.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Year 8: Bounds Dr J Frost (jfrost@tiffin.kingston.sch.uk) Last modified: 20th June 2014
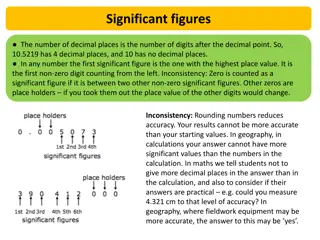
Starter Write down the number 24.98063 to the following number of significant figures: ? ? ? ? ? 1sf 20 2sf 25 3sf 25.0 (the .0 is required!) 4sf 24.98 5sf 24.981 The length of a squirrel is measured as 14cm correct to the nearest cm. What is the smallest possible length the squirrel could be? What is the largest possible length? ? Smallest possible length: 13.5cm 14.5cm* ? Largest possible length:
More Squirreling For a length of 14cm measured, the range of possible values was 13.5cm to 14.5cm. Lower Bound: Upper Bound: 13.5cm 14.5cm Question 1: How would we represent the range of possible values on a number line? ? 12cm 13cm 14cm 15cm The value of 14.5cm isn t include, because this would have rounded to 15cm.
Activity In pairs, work on the handout. Value 7cm 5.3m 200km 8.04mm Accuracy Nearest cm Nearest 0.1m Nearest 10km Nearest hundredth of a mm Nearest cm 2sf 3sf 1sf Lower Bound 6.5cm 5.25m 195km 8.035mm Upper Bound 7.5cm 5.35m 205km 8.045mm ? ? ? ? ? ? ? ? ? ? ? ? ? ? 3m 830 litres 830 litres 100 miles 2.995m 825 litres 829.5 litres 95m 3.005m 835 litres 830.5 litres 150m Can you think of an easy way of getting the bounds given the accuracy?
Easily getting bounds To find bounds, just add or subtract half the accuracy! Value: 250m Correct to: nearest 10m ? ? Lower Bound = 250 (10/2) = 245m Upper Bound = 250 + (10/2) = 255m Value: 423mm Correct to: tenth of a mm ? ? Lower Bound = 423 (0.1/2) = 423.05mm Upper Bound = 423 + (0.1/2) = 422.95mm
Exercises A laser measures a distance and displays 3 metres to some given degree of accuracy. Find the lower and upper bound when the accuracy was: To the nearest metre. ?.?? ?.?? To the nearest cm. ?.???? ?.???? To the nearest mm. ?.????? ?.????? 1 ??? An Events Organiser is planning a concert is told that a stadium has a capacity of 30,000, correct to 1 significant figure. The organiser want to ensure that anyone he sells tickets to is guaranteed a seat. How many tickets can he sell? 25000 2 ? The length of an ant is 6.54cm correct to 2 decimal places. Calculate the upper and lower bounds. ?.?????, What if the length in Question 3 was correct to 3 decimal places? ?.??????, 3 ? ?.????? 4 ? ?.?????? The distance travelled by a runner is 100m correct to the nearest metre and their time 9.7s correct to the nearest 0.1s. What s their slowest possible average speed? ? = ???.? ?.?? = ??.???/? A cube is 10m3 correct to 1 significant figure. What is the maximum and minimum possible side length? ????? ????? = ? ? ??? = ?.???? ??.? = ?.???? ????? ????? =