Understanding Hooke's Law for Elastic Springs
Robert Hooke discovered Hooke's Law, stating that the extension of a spring is directly proportional to the tension applied to it, with a constant called stiffness. The modulus of elasticity is the inverse of the natural length of the spring. By applying the formulas derived from Hooke's Law, you can calculate parameters like modulus of elasticity, tension, stiffness, and natural length of springs accurately in various scenarios discussed in the content.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
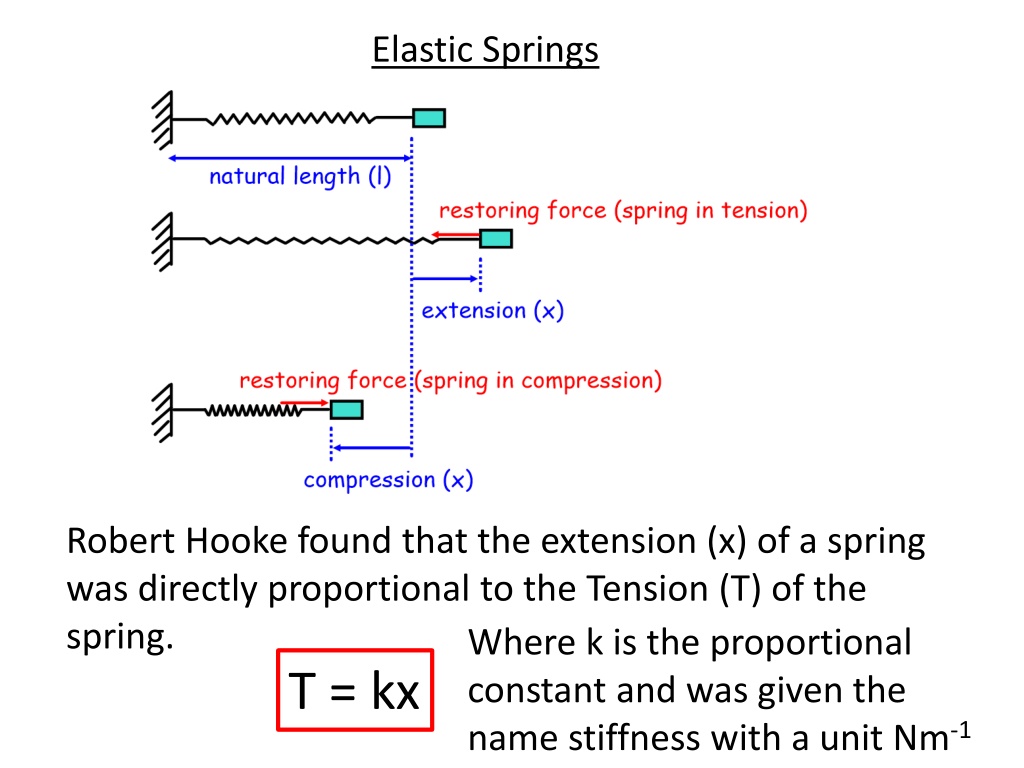
Elastic Springs Robert Hooke found that the extension (x) of a spring was directly proportional to the Tension (T) of the spring. T = kx constant and was given the name stiffness with a unit Nm-1 Where k is the proportional
Hooke also found that this constant was inversely proportional to the natural length(l) of the string. Where the constant is now called the modulus of elasticity which is measured in Newtons. T = x l These two formula for the tension of a spring are known as Hooke s Law
1) An elastic rope is extended by 20% when it is used to secure goods on a lorry. If the tension on the rope is 140N what is the modulus of elasticity? T = x l 140 = 0.2l l 140 = 0.2 = 140 0.2 = 700N
2) The spring in suspension exerts a thrust of 3kN when it is compressed to a length of 17.5cm. The modulus is 24kN. Find its natural length. T = x l 3000 = 24000(l 0.175) l 3000l = 24000(1 0.175) l = 8l 1.4 -7l = 1.4 l = 0.2m l = 24000(l 0.175) 3000 l = 8 (l 0.175)
3) A tension of 3N produces an extension of 2.5cm in an elastic string. Find a) The stiffness k b) The tension when the extension is 15cm. T = kx 3 = k x 0.025 k = 120 Nm-1 T = kx T = 160 x 0.15 T = 24N
4) A particle P is attached to the midpoint of a light elastic spring of natural length 0.5m and modulus 56N. The ends of the string are fixed at points A and B which are on the same horizontal level and 0.6m apart. When in equilibrium AP and PB are inclined 60o to the horizontal. Find the mass of the particle. T = x Resolve vertically 0.6m T1 = T2 cos 60 = 0.3 A B l 60o 60o mg = 2 x 78.4sin60 T = 56x0.7 AP 0.5 0.3 cos60 mg = 135.79 AP = T = 78.4N T1 T2 m = 13.856 AP = 0.6m m = 13.9kg x + l = 0.6 x 2 P x + l = 1.2 x = 1.2 0.5 x = 0.7m mg
5) A tennis ball of mass 60g is attached to a post in a garden by an elastic string of natural length 3m. When using this equipment for practice a player holds the ball so that the string is horizontal and stretched by 15cm. If the force applied to the ball by the player is F newtons acting at 15o above the horizontal find: a) The value of F b) The modulus of the string. Resolve horizontally Resolve vertically F 0.06g = Fsin15 F = 0.06g sin15 T = Fcos15 T = x l = Fcos15 0.15 3 = 2.27cos15 = 43.9N T 15o F = 2.27 N 0.06g
6) A body of mass Mkg lies on a smooth horizontal surface and is connected to a point O on the surface by a light elastic string of natural length 50cm and modulus 70N. When the body moves in a horizontal circular path about O with a constant speed of 3.5ms-1 the extension of the string is 20cm. Find the mass of the body. T = mv2 T = x R l r T = 700.2 28 = Mx3.52 0.5 0.7 O T = 28N 28 = 17.5M 0.7m Mg M = 1.6kg
Energy Stored in a Spring We know that Work done is equal to the Force x distance however the Force varies with the distance so you can integrate to find the Work done or find the average Force and use that. F at O = 0N F at x = x lN Average Force = (0 + x l) 2 = x 2l This Work done can also be found using the stiffness k. F at x = kxN F at O = 0N Average Force = (0 + kx) 2 = kx Work done = x 2 2 x x 2l x x Work done = kx Work done = x2 Work done = kx2 2l 2 Ep= x2 2l = kx2 This Work done is in the form of Potential Energy. 2
The firing mechanism in a pinball machine contains a spring of natural length 4cm whose modulus is 10N. The work done im compressing the spring is 0.05J. By how much is the spring compressed? Ep= x2 2l x2 0.05 = 10 2x0.04 x2 = 0.05 x 2 x 0.04 10 x2 = 0.0004 x = 0.02m
Conservation of Energy in a Spring The principles of conservation of energy of course also applies to springs i.e. the sum of the potential and kenetic energies are always constant in a system. Potential Energy from gravity Potential Energy from spring Kinetic Energy from movement Constant Value Total Energy = = + + ET = EP + EEP + EK
A particle P of mass 0.5kg is attached to one end of a light elastic string of natural length 40cm and modulus 7N. The other end is attached to a fixed point O. The particle is released from rest at the point A, which is 1m vertically below O. Find the velocity of the particle when the string becomes slack. Initial Position Position ET = EP + EEP + EK ET = 0 + x2 Initial Energy Energy at B ET = EP + EEP + EK Slack O O 2l+ 0 0.62 2 x 0.4 3.15= (0.5gx0.6) + 0+ 1 20.5v2 0.4m ET = 7 1m 3.15 = 2.94 + 0.25v2 B ET = 3.15J 0.21 = 0.25v2 v2 = 0.84 v= 0.92ms-1 A 0.5g 0.5g
A toy engine has a mass of 800g. When it reaches a buffer at the end of the line it is travelling at 0.1ms-1. The buffer consists of a spring of natural length 3cm and modulus 4.5N. Find the compression in the spring when the engine comes to rest. EK = EP = x2 Engine s energy v = 0.1ms-1 2l EK = 1 EK = 1 2 mv2 0.004 = 4.5x2 2x0.03 2 x 0.8 x 0.12 x2= 0.0000533 EK = 0.004J 0.03m m = 0.8kg x = 0.0073029 No Ep as movement is horizontal x = 0.0073m x = 7.3mm
A man, of mass 70kg is going to carry out a sponsored bungee jump from a bridge. The bridge is 64m above the river which flows beneath. The rope he intends to use has a modulus of 4kN. Taking g = 10ms-2 find the natural length of the rope needed if he plans to fall a distance of 60m. When on bridge ET = 0J At lowest point 4000x(60 l)2 2l - 42 000 = 0 EK = 0J 4000x(60 l)2 2l = 42 000 60m EP = mgh m = 70kg 3600 120l + l2 = 84000 l EP = 70x10x(-60) 4000 EP = -42 000J EP = x2 2l 3600 120l + l2 = 21l l2 141l +3600 = 0 Use quad formula EP = 4000x(60 l)2 2l l = 33.48m or 107.52m
The previous example ignore air resistance. However if a constant force of 80N opposed the motion the solution is altered: 4000x(60 l)2 2l - 42 000 + 4800 = 0 80N 4000x(60 l)2 2l 60m = 37200 m = 70kg 3600 120l + l2 = 74400 l 4000 3600 120l + l2 = 18.6l l2 138.6l +3600 = 0 WD by air = F x d Use quad formula WD by air = 80 x 60 l = 34.3m or 103.7m WD by air = 4800J
Newtons Law of Restitution If a ball is dropped from a certain height the height to which it bounces back will depend on the material of the ball and the surface it is bouncing on. In general the speed after the collision will be less than before the collision: v = e x u u is the speed before and e coefficient of restitution This is Newton s Law of Restitution e must always be smaller than 1 as the speed after is less so 0 e 1. If e = 1 this is called a perfectly elastic collision. Where v is the speed after Add speeds if travelling away from each other If e = 0 this is called an inelastic collision. The coefficient of restitution can be found by using the speeds before and after the collision: difference in speeds after difference in speeds before = v2 v1 e = u2 u1 or v2 v1 = e(u2 u1)
The diagram illustrates collisions between smooth spheres with identical radius. Calculate e between each pair of spheres: v2 = 1.5ms 1 v1 = 0.5ms 1 u2 = 1ms 1 u1 = 3ms 1 a) after before v1 = 1ms 1 v2 = 1.5ms 1 u1 = 3ms 1 u2 = 0ms 1 b) before after e = v2 v1 u1 u2 e = v2 + v1 u1 u2 a) b) e = 1.5 0.5 3 1 e = 1 + 1.5 3 0 e = 5 6 e = 1 2
Two smooth spheres A and B are travelling towards each other with speeds of 0.1ms-1 and 0.4ms-1. After impact the direction of A is reversed and its speed doubled. If e = 0.6, what is the speed of B. after before u2 = 0.4ms 1 v1 = 0.2ms 1 v2 = ? u1 = 0.1ms 1 v1 + v2 = e(u1 + u2) 0.2 + v2 = 0.6(0.1 + 0.4) v2 = (0.6 x 0.5) 0.2 v2 = 0.1ms-1
A smooth sphere is travelling with a speed of 5ms-1 towards a vertical wall. After impact with the wall it rebounds with an initial speed of 4ms-1. Calculate the coefficient of restitution. after before v1 = 4ms 1 u1 = 5ms 1 e = v1 + v2 u1 + u2 e = 4 + 0 5 + 0 e = 4 5
A smooth sphere of mass 4m is travelling in a straight line on a horizontal table. It collides with another sphere with identical radius and mass 8m moving on the same straight line but in the opposite direction. Before collision, the speed of A is u ms-1 and B 0.6ms-1. After A s speed is doubled and reversed. Given e 1 2= determine the speeds of both spheres after impact. u1 u2 = 0.6ms 1v1 = 2u1 4m 8m v2 = ? 4m 8m before after Use Law of Restitution: Use principle of conservation of momentum: 4m x u1 + 8m x (-0.6) = 4m x (-2u1)+ 8m x v2 v1 + v2 = e(u1 + u2) 2u1 + v2 = 0.5(u1 + 0.6) 4u1 + 2v2 = u1 + 0.6 3u1 + 2v2 = 0.6 4mu1 4.8m = -8mu1 + 8mv2 u1 1.2 = -2u1 + 2v2 3u1 - 2v2 = 1.2 Use simultaneous equations to solve:
3u1 - 2v2 = 1.2 3u1 + 2v2 = 0.6 1 2 Sub v2 = -0.15ms-1 in 1 - 2 1 3u1 2(-0.15) = 1.2 3u1 + 0.3 = 1.2 4v2 = -0.6 v2 = -0.15ms-1 3u1 = 0.9 u1 = 0.3ms-1 Therefore both spheres are moving to the left with respective speeds of 0.6ms-1 and 0.15ms-1.
Simple Harmonic Motion Simple Harmonic Motion occurs when an object is displaced in one direction from a position of rest, travels back through that position to the same displacement on the other side. For example, a floating cork pushed under the surface or a child pushed on a swing or a model plane on a vertical sping which is pulled down and released. In practice each of these would come to rest due to resistance to motion however if there was no resistance then the oscilation would go on forever. This movement is called Simple Harmonic Motion (SHM). The distance from the centre of motion to the end of the path is called the amplitude (A). The resultant force acting on the body increases the further it is from the centre and hence the greater the acceleration.
Linear SHM is motion which the acceleration is directed towards a fixed point and is proportional to the distance from the fixed point (the centre of oscillation). SHM is a form of circular motion, using the eqution for displacement from circular motion: x = A sin t Differentiating gives v = A cos t Differentiating again gives a = - A 2 sin t Replace with x we get a = - 2 x 2 is the constant of proportionality in SHM
Seven SHM formulae to remember: x = Asin( t + ) a = - 2 x is the constant of integration v = A cos( t + ) v2 = 2(A2 x2) T = 2 T is the period or periodic time vmax = A amax = - 2A
1) Find the maximum speed and acceleration of a particle moving with SHM of period 4 and amplitude 25cm = T = 2 4 = 8 vmax = A vmax = 8 x 0.25 vmax = 2ms-1 amax = - 2A amax = -(8)2 x 0.25 amax = -16ms-2
2) A particle moves with SHM about O. When it is 50cm from O its speed is 3.6ms-1 and when it is 120 cm from O its speed is 1.5ms-1. Find the amplitude and period of motion v2 = 2(A2 x2) 3.62 = 2(A2 0.52) You can multiply out and use simultaneous equations or a shortcut is to divide the two equations. 3.62 1.52 = 2(A2 0.52) 2(A2 1.22) 3.62 1.52 = A2 0.52 A2 1.22 3.62(A2 1.22) = 1.52(A2 0.52) v2 = 2(A2 x2) 1.52 = 2(A2 1.22) 10.71A2= 18.0999 A2= 1.69 A = 1.3m 1.52 = 2(1.32 1.22) 1.52 = 0.25 2 9 = 2 3.62A2 (3.62x1.22) = 1.52A2 (1.52x0.52) = 3
A = 1.3m = 3 T = 2 T = 2 secs 3
Springs and Simple Harmonic Motion 1) A particle, P, of mass 1.5kg is attached to one end of a spring of natural length 50cm and modulus 6N. The other end, O, is attached to a point on a smooth horizontal surface. P is held at rest on the surface with OP = 0.75m and then released. Show P performs SHM and find the maximum acceleration. At equilibrium x = 0.75 - 0.5mO P O m = 1.5kg m = 1.5kg l = 0.5m If this system gives an equation in the form of a = - 2 x this proves SHM occurs.
T x = 0.75 - 0.5mO P m = 1.5kg 2= 8 = 8 = 2 2 T = - x l = ma -6 x ? 0.5 = 1.5a A will be the initial displacement A = 0.25m -12x = 1.5a a = -8x amax = -( 8)2 x 0.25 This is in the form of a = - 2 x therefore SHM occurs. amax = -2ms-2
2) A light elastic spring of natural length 50cm and modulus 20gN, hangs vertically with its upper end fixed and a body of mass 6kg attached at the other. The body initially rests in equilibrium but is then pulled down 0.25m and released. Show the motion is SHM and find the period of motion and maximum speed. Find extension at equilibrium T = x l = mg 20ge 0.5 = 6g 40e = 6 e = 0.15m 0.5m T e Equilibrium point 0.25m After using balance of Forces mg T = ma 6g 20g0.15+? 0.5 = 6a 6g 40g(0.15 + x) = 6a m = 6kg -40gx = 6a a = 40gx 6g 6 In the form of a = - 2 x SHM occurs. 6g (6g + 40gx) = 6a
Extension beyond equilibrium is 0.25m therefore Amplitude is 0.25m. 0.5m T a = 40gx e Equilibrium point 6 0.25m 2= 40g m = 6kg 6 6 = 14 vmax = A vmax = 14 vmax = 14 vmax = 7 vmax = 7 3 = 40g 6g 3 3x0.25 T = 2 14 3 4 3 T = 3 2 3 secs 7 6ms-1
3) A light elastic string of natural length 2.4m and modulus 15N is stretched between two points A and B 3m apart on a smooth horizontal surface. A body of mass 4kg is attached at the midpoint. The mass is then stretched 10cm towards B. Show that the motion is SHM, find the speed of the body 158cm from A. 1.2m0.3m 1.2m0.3m 0.1m T1 T2 T1 T2 A A B B 1.5m 1.5m 1.5m 1.5m Equilibrium point Equilibrium point Using balance of Forces 3.75 - 12.5x (3.75 + 12.5x) = 4a T1 T2 = ma 15x0.3 ? -25x = 4a a = 25x 1.2 - 15x0.3+? In the form of a =- 2x SHM occurs. 1.2 = 4a 4
At 158cm from A x = 0.08m. A = 0.1m v2 = 2(A2 x2) v2 = 25 (0.12 0.082) 4 v2 = 0.0225 v = 0.15ms-1
4) On a smooth horizontal surface points A and B are 3.1 metres apart. A body with mass of 5kg sits between them. A light elastic string of natural length 1.1m and modulus 22N joins point A to the body and another with natural length 80cm and modulus 8N joins B and the body. If the body is moved 30cm towards A and released show that SHM occurs and find the velocity when the body is 1.7m from A. Equilibrium point 1 = 22N At equilibrium T1 = T2 2 = 8N 1x1 1.1 = 8x2 l1 = 2x2 l2 l2 = 0.8m T2 l1 = 1.1m T1 22x1 5kg 0.8 B A 20 x1 = 10 x2 2x1 = x2 3.1m 1.1 + x1 + 0.8 + x2 = 3.1 x1 + x2 = 1.2 x1 + 2x1 = 1.2 Sub in 2x1 = x2 x1 = 0.4m x2 = 0.8m
Equilibrium point 0.3m 2 = 8N 1 = 22N l2 = 0.8m T2 l1 = 1.1m T1 5kg B A 3.1m 1.1m 0.4m 0.8m 0.8m 1.7m 0.2m Using balance of Forces T1 T2 = ma 22x0.4 ? 2 = 6 = 6 A= 0.3m x= 0.2m v2 = 2(A2 x2) v2 = 6(0.32 0.22) 1.1 - 8x0.8+? 8 - 20x (8 + 10x) = 5a 0.8 = 5a v2 = 0.3 v = 0.55ms-1 -30x = 5a a = -6x In the form of a =- 2x SHM occurs.
A Simple Pendulum If a particle of mass m kg is suspended from a fixed point by a light inextensible string of length l metres, the motion of the mass when moved would be SHM. The Period of the SHM is given by: l l g TP= 2 x This formula can be derived.
Definition of a Radian A radian is the angle made by taking the radius and wrapping it round the circle. r One Radian is (180/ ) degrees, which is about 57.2958 degrees. (in radians) = arc length (x) x radius (?)
Deriving The Period of A Simple Pendulum F is the force along the tangent of the swing back towards the vertical positionF = - mg sin For small values of in radians sin l F = - mg F = - mg x a = F m a = - g x 2 = g l x l g l = mg Tp = 2 Tp = 2 The Tension in the string may include mv2 l a = -g r l x g l In the form of a =- 2x SHM occurs. l g Tp = 2