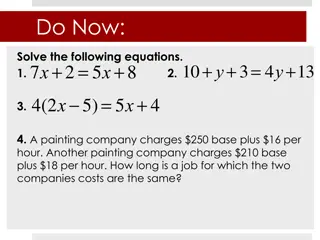Solving Systems of Equations by Elimination
undefined
Warm Up/Activating Strategy
1.
Find the numbers that make the equations true for the following.
____ +
__-5__
= 0
__2_
+ ____ = 0
+ ____ = 0
(___)_
(___)_
5
5
_ +
_ +
_-10
_-10
_ = 0
_ = 0
2.
In your own words what do you see that is unique about the
In your own words what do you see that is unique about the
numbers that equal to zero?
numbers that equal to zero?
What are these numbers called?
1.
Arrange
the equations with like terms
in columns
2.
Multiply
, if necessary, to create
opposite coefficients for one variable.
3.
Add
the equations.
4.
Substitute
the value to solve for the
other variable.
5.
Check
4x + 3y = 16
2x – 3y = 8
3x + 2y = 7
-3x + 4y = 5
2x – 3y = 4
-4x + 5y = -8
2x + 3y = 1
4x – 2y = 10
5x + 2y = 7
-4x + y = –16
Please solve the first set of practice problems #1-9. I
have provided an answer key. Here is a link for
instructions if you need help working them out.
The second set of problems you will work on your
own. I will provide key so you can check as you go.
Please free to ask questions.
You will be assigned 5 questions at the end of the
lesson to turn in.
Use elimination to solve each system of equations.
1.
6x + 5y = 4
2. 3m – 4n = -14 3. 3a + b = 1
6x – 7y = -20
3m + 2n = -2 a + b = 3
4.
-3x – 4y = -23 5. x – 3y = 11 6. x – 2y = 6
-3x + y = 2 2x – 3y = 16 x + y = 3
7.
2a – 3b = -13
8. 4x + 2y = 6
9. 5x – y = 6
2a + 2b = 7 4x + 4y = 10
5x + 2y = 3
Set 2
Set 2
Use elimination to solve each system of equations.
1.
2x + 3y = 6
2. 2m + 3n = 4 3. 3a - b = 2
x + 2y = 5
-m + 2n = 5 a + 2b = 3
4.
4x + 5y = 6
5. 4x – 3y = 22 6. 3x – 4y = -4
6x - 7y = -20 2x – y = 10 x + 3y = -10
7.
4x – y = 9
8. 4a – 3b = -8
9. 2x + 2y = 5
5x + 2y = 8 2a + 2b = 3
4x - 4y = 10
Practice
Practice
Worksheet
Worksheet
Learn how to solve systems of equations by elimination method through examples, warm-up exercises, steps for elimination, and practice problems. Master this technique to find the unique values that make the equations true. Get ready to enhance your algebra skills with step-by-step guidance and visual aids.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
EQ: How do we solve Systems of Equations by Elimination?
Warm Up/Activating Strategy 1. Find the numbers that make the equations true for the following. ____ + __-5__ = 0 __2_ + ____ = 0 (___)_5_ + _-10_ = 0 2. In your own words what do you see that is unique about the numbers that equal to zero? What are these numbers called?
Steps for Elimination: 1. Arrange the equations with like terms in columns 2. Multiply, if necessary, to create opposite coefficients for one variable. 3. Add the equations. 4. Substitute the value to solve for the other variable. 5. Check
EXAMPLE 1 (continued) 2 2 x x 2 2 y y 8 + = = 4 (-1, 3)
EXAMPLE 2 4x + 3y = 16 2x 3y = 8 (4, 0)
EXAMPLE 3 3x + 2y = 7 -3x + 4y = 5 (1, 2)
EXAMPLE 4 2x 3y = 4 -4x + 5y = -8 (2, 0)
EXAMPLE 5 2x + 3y = 1 4x 2y = 10 (2, -1)
EXAMPLE 6 5x + 2y = 7 -4x + y = 16 (3, -4)
Classwork Please solve the first set of practice problems #1-9. I have provided an answer key. Here is a link for instructions if you need help working them out. The second set of problems you will work on your own. I will provide key so you can check as you go. Please free to ask questions. You will be assigned 5 questions at the end of the lesson to turn in.
Practice Problems Set 1 Use elimination to solve each system of equations. 1. 6x + 5y = 4 2. 3m 4n = -14 3. 3a + b = 1 6x 7y = -20 3m + 2n = -2 a + b = 3 1, 4) 2, 2) 1, 2) 4. -3x 4y = -23 5. x 3y = 11 6. x 2y = 6 -3x + y = 2 2x 3y = 16 x + y = 3 (1, 5) 7. 2a 3b = -13 8. 4x + 2y = 6 2a + 2b = 7 4x + 4y = 10 (5, 2) (4, 1) 9. 5x y = 6 5x + 2y = 3 1/2, 4) (1/2, 2) (1, 1)
Set 2 Practice Problems Use elimination to solve each system of equations. 1. 2x + 3y = 6 2. 2m + 3n = 4 3. 3a - b = 2 x + 2y = 5 -m + 2n = 5 a + 2b = 3 (1, 1) 1, 2) 3, 4) 4. 4x + 5y = 6 5. 4x 3y = 22 6. 3x 4y = -4 6x - 7y = -20 2x y = 10 x + 3y = -10 1, 2) (4, 2) 4, 2) 7. 4x y = 9 5x + 2y = 8 2a + 2b = 3 8. 4a 3b = -8 9. 2x + 2y = 5 4x - 4y = 10 (2, 1) 1/2, 2) (2.5, 0)
Homework Practice Worksheet
