Simplified Linear Transformation for N Application Rates in Corn and Wheat

Dr. Brenda Ortiz and Dr. Bill Raun led an investigation on predicting grain yield using optical sensors in corn and wheat. The challenges with the symmetric sigmoid model for yield prediction led to the development of a simplified linear transformation approach. Assumptions were made to create a model linking NDVI and crop yield, emphasizing linearity in a specific region. Despite concerns about complex nonlinear models, the need for N-Lin models in agriculture remains, including the use of the symmetric sigmoid growth model.

• Corn
• Wheat
• Linear Transformation
• N Application Rates
• Optical Sensors

lasseter_j Follow

Uploaded on Sep 11, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. A Simplified Linear Transformation to Calculate N Application Rates in Corn and Wheat

2. Dr. Brenda Ortiz Who Built The Unique Corn Optical Sensor Data Set Required for This Investigation And Dr. Bill Raun Who Kept this Investigation going Through Hell and High Water Dr. Jim Schepers Whose argument for measuring NDVI at Two Different Locations Without an N Rich Strip caused me to Modify my approach to the problem.

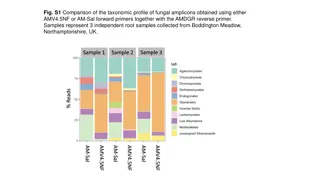
3. Corn at three growth stages symmetric sigmoid model 6.00 5.00 Yield Goal, mg/Ha 4.00 3.00 Meas.GS V-6 Meas.GS V-8 Meas.GS V-10 2.00 GS V-6 GS V-8 1.00 GS V-10 0.00 0 0.2 Normalized Difference Vegetative Index 0.4 0.6 0.8 1

4. Difficulty with the symmetric sigmoid for predicting grain yield This equation is Parametric each parameter is a function of an equation. This means that you cannot directly solve for any value of the yield equation. This isn t good. We must adjust the parameters until the equation predicts known yield values. Consequently, we can t directly solve the yield equation for exact values. We need a simpler approach which replaces parameters with constants and linearizes the relationship between the independent dependent variable (FP ndvi) and the dependent variable yield.

5. We can make the following assumptions when developing We can make the following assumptions when developing a model to predict grain yield with optical sensors a model to predict grain yield with optical sensors Yield without additional N is proportional to Farmer Practice NDVI. NRich NDVI is independent of location within an area in a field where production variables exhibit geostatistical relatedness. A straight line can be constructed between the maximum value of NRich NDVI and the minimum value of Farmer Practice NDVI. Because NDVI is linearly proportional to crop yield, a straight line can be fit through NDVI and crop Yield. (Dr. Jim Schepers)

6. Corn and Wheat there is a region where symmetric sigmoid exhibits high linearity 6.00 5.00 Yield Goal, mg/Ha 4.00 3.00 2.00 1.00 0.00 0 0.2 Normalized Difference Vegetative Index 0.4 0.6 0.8 1

7. linearization Despite the concerns about using sophisticated non-linear models, agronomist have need to use N-Lin models to describe and predict complex biological phenomena. One of these model is the symmetric sigmoid which is a step function i.e. growth models. Many of these models are parametric requiring input of data to change values of coefficients as inputs change. In effect, two, three, or more additional equations are needed to define the coefficients required to implement the non-linear model. One approach often used by engineers when creating models to control machines and processes, is to break the model up into segments which can be treated as independent models within the range of interest. In the case of symmetric sigmoid, most of the change in the value of the dependent variable occurs for NDVI values ranging form 0.20 and 0.80. Nearly all change occurs between 0.10 and 0.90 NDVI.

8. Consistently, yield data were linear functions of NDVI

9. Data Linearization Fit a straight line (linear regression) through the data Fit a straight line through at least two N-Rich reference strips Locate one NRich strip in the highest yielding portion of the field and one from the natural occurring lowest producing area of the field. Exclude alkali spots, pot-holes, abnormally low producing regions, etc. Although only two carefully selected areas are needed to establish the linear regression line, additional N-Rich strips will improve the accuracy and precision of the fitted straight line.

10. Linearized Generalized N Rate Algorithm AONR Corn Experiment - 2014 0.9 0.8 0.7 Yield Goal Plateau Normalized Yield 0.6 0.5 0.4 0.3 Linearized Yield Goal 0.2 0.1 0 0 0.2 0.4 0.6 0.8 1 Normalized Difference Vegetative Index

11. NDVI Farmer Practice vs NRich NDVI 23 Site Years 1.0000 0.9000 0.8000 0.7000 N Rich NDVI 0.6000 0.5000 0.4000 y = 0.5411x + 0.4364 R = 0.3956 0.3000 0.2000 0.1000 0.0000 0.0000 0.2000 Farmer Practice NDVI 0.4000 0.6000 0.8000 1.0000

12. 6 LCB 2004 109 1416 5 y = 5.895x - 0.2524 R = 0.5905 Wheat Yield, t/Ha 4 3 2 1 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Farmer Practice NDVI

13. Efaw 2004 75 846 6 5 Corn Yield mT/HA 4 3 2 y = 10.941x - 1.1069 R = 0.5882 1 0 0 0.1 0.2 0.3 0.4 0.5 NDVI 0.6 0.7 0.8 0.9 1

14. Why Linearize Data Establishes a straight line relationship between NDVI and Grain Yield. Differences between NDVI values are equivalent to differences in yield. Yield goal is the maximum expected yield

15. Additional Steps NDVI of the yield goal for the most productive area and for the least productive area must be determined using an N-Rich reference strip. Although peak yield generally occurs at approximately 0.80 NDVI, there is no guarantee that it will. A second N-Rich reference strip must be established in the least productive area in the field. Yield goals must be established at each location. The literature contains several methods for establishing reasonable yield goals. A linear curve must be fitted to the data with NDVI being the independent variable and yield goal being the dependent variable. Use standard regression equations for linear curves.

16. Corn - 57-gd,Haskell 2004, 99day 14.00 y = 15.491x - 2.0775 R = 0.7334 12.00 10.00 Corn Yield mT/Ha 8.00 6.00 Yield Goal 4.00 MinYld=Yld Goal*0.48/0.81 2.00 0.00 0 0.2 0.4 0.6 0.8 1 NDVI

17. Corn - 57-gd,Haskell 2004, 99day Defines the yield limit without additional N. Increase in yield will be proportional to increase in NDVI 14.00 y = 15.491x - 2.0775 R = 0.7334 12.00 10.00 Corn Yield mT/Ha 8.00 6.00 4.00 2.00 0.00 0 0.2 0.4 0.6 0.8 1 NDVI

18. 56-gd, Efaw OFFIt, 2006 Circles are approximate locations for Nrich NDVI and minimum NDVI 14.00 Expected Yield mT/Ha 12.00 y = 26.348x - 10.101 R = 0.3986 10.00 8.00 6.00 4.00 2.00 0.00 0 0.2 0.4 0.6 0.8 1 NDVI

19. Appendix Additional Examples

20. 12.00 52-gd, LCB N Study 2006 10.00 y = 24.321x - 9.5855 R = 0.477 8.00 Corn Yield mg/Ha 6.00 4.00 2.00 0.00 0 0.2 0.4 NDVI 0.6 0.8

21. 57-gd, Haskel 2004, 113 Day Corn 14.00 12.00 Corn Yield mT/Ha y = 21.178x - 6.3523 R = 0.5878 10.00 8.00 6.00 4.00 2.00 0.00 0 0.2 0.4 NDVI 0.6 0.8 1

22. 53-gd, LCB Catchup 2005 16.00 14.00 Corn Yield mT/Ha 12.00 10.00 8.00 y = 54.362x - 33.409 R = 0.4606 6.00 4.00 2.00 0.00 0.78 0.8 0.82 0.84 0.86 0.88 NDVI

23. 61-gd, Haskell 2004, 115 Day 14.00 12.00 y = 28.192x - 12.357 R = 0.5474 10.00 Corn Yield mT/Ha 8.00 6.00 4.00 2.00 0.00 0 0.2 0.4 0.6 0.8 1 NDVI

24. TVS BT 2009- 709 GDD GCS ST 2009- 712 GDD 14.0 10.0 9.0 12.0 8.0 y = 12.734x + 1.202 R = 0.2311 y = 36.344x - 6.5653 R = 0.6287 10.0 Corn Yield, mT/ha 7.0 Corn Yield, mT/ha 6.0 8.0 5.0 6.0 4.0 4.0 3.0 2.0 2.0 1.0 0.0 0.0 0.0000 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.0000 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 Farmer Practice NDVI Farmer Practice NDVI EVS ST 2010- 883 GDD EVS BT 2010- 1106 GDD 10 10.0 9 y = 26.431x - 7.8409 R = 0.7382 9.0 8 8.0 Corn Yield , mT/Ha 7 y = 18.834x - 5.6357 R = 0.3182 7.0 Corn Yield, mT/Ha 6 6.0 5 5.0 4 4.0 3 3.0 2 2.0 1 1.0 0 0.0000 0.0 0.1000 0.2000 0.3000 Farmer Practice NDVI 0.4000 0.5000 0.6000 0.7000 0.0000 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Farmer Practice NDVI

25. TVS BT 2011- 844 GDD EVS BT 2011- 879 GDD 6.0 12.0 Corn Yield, mT/HA 5.0 Corn Yield, mT/Ha y = 24.706x - 12.037 R = 0.4469 10.0 y = 9.0009x - 2.7958 R = 0.1896 4.0 8.0 3.0 6.0 4.0 2.0 2.0 1.0 0.0 0.0 0.0000 0.0000 0.2000 0.4000 0.6000 0.8000 1.0000 0.2000 0.4000 Farmer Practice NDVI 0.6000 0.8000 1.0000 Farmer Practice NDVI EVS BT 2012 - 773 GDD EVS ST 2012- 773 GDD 12.0 10.0 Corn Yi,eld, mT/Ha Corn Yield, mT/Ha 10.0 9.0 y = 30.878x - 17.498 R = 0.6082 8.0 8.0 7.0 6.0 6.0 5.0 4.0 4.0 y = -3.1691x + 9.3598 R = 0.0066 3.0 2.0 2.0 1.0 0.0 0.7000 0.0 0.7500 Farmer Pactice NDVI 0.8000 0.8500 0.0000 0.2000 0.4000 0.6000 0.8000 1.0000 Farmer Practice NDVI

26. Corn - 57-gd,Haskell 2004, 99day 14.00 y = 15.491x - 2.0775 R = 0.7334 12.00 10.00 Corn Yield mT/Ha 8.00 6.00 4.00 2.00 0.00 0 0.2 0.4 0.6 0.8 1 NDVI

27. 6 LCB 2004 109 1416 5 y = 5.895x - 0.2524 R = 0.5905 Wheat Yield, t/Ha 4 3 2 1 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Farmer Practice NDVI

28. Efaw2004 124 1521 7 6 y = 6.8536x - 1.3034 R = 0.9225 124-GD 5 Corn Yld, mT/Ha TC Model 4 Linear (124-GD) 3 2 1 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 NDVI