Shape Enlargement and Transformation
E
n
l
a
r
g
e
t
h
i
s
s
h
a
p
e
u
s
i
n
g
s
c
a
l
e
f
a
c
t
o
r
:
(a) 2
(b) 4
(c) 1
(d) 0.5
E
n
l
a
r
g
e
t
h
i
s
s
h
a
p
e
u
s
i
n
g
s
c
a
l
e
f
a
c
t
o
r
:
(a) 2
(b) 4
(c) 1
(d) 0.5
A:(6,6) B:(6,3) C:(12,3) D:(12,6)
You should have a rectangle.
A
D
C
B
Plot the coordinates, join them up and label the vertices
A:(6,6) B:(6,3) C:(12,3) D:(12,6)
A
D
C
B
Label the new vertices A’, B’, C’ and D’
D’
A’
C’
B’
What can we
say about
the new
shape?
Can you include these
words in your discussion?
Scale
Vertices
Centre
Angles
Congruent
A
D
C
B
D’
A’
C’
B’
The
centre of enlargement
is
(0,0)
A
D
C
B
D’
A’
C’
B’
The
centre of enlargement
is
(0,0)
“
DON’T
RUB ME
OFF”
A
D
C
B
D’
A’
C’
B’
“
DON’T
RUB ME
OFF”
A:(6,6) B:(6,3) C:(12,3) D:(12,6)
A
D
C
B
Label the new vertices A’, B’, C’ and D’
What is the same?
What is different?
D’
C’
B’
A’
Can you
include
these words
in your
discussion?
Scale
Centre
Vertices
Intersect
A:(6,6) B:(6,3) C:(12,3) D:(12,6)
A
D
C
B
Label the new vertices A’, B’, C’ and D’
Counting squares
to check
D’
C’
B’
A’
A
D
C
B
D’
C’
B’
A’
S
h
a
p
e
1
A
(
-
9
,
6
)
B
:
(
-
9
,
2
)
C
:
(
-
5
,
2
)
D
:
(
-
5
,
6
)
S
h
a
p
e
2
A
’
:
(
-
9
,
1
)
B
’
:
(
-
9
,
-
1
)
C
’
:
(
-
7
,
-
1
)
D
’
:
(
-
7
,
1
)
Where is the
centre of
enlargement?
Draw the two shapes and label the vertices
A
D’
C’
B’
A’
D
C
B
“
DON’T
RUB ME
OFF”
S
h
a
p
e
1
A
(
-
9
,
6
)
B
:
(
-
9
,
2
)
C
:
(
-
5
,
2
)
D
:
(
-
5
,
6
)
S
h
a
p
e
2
A
’
:
(
-
9
,
1
)
B
’
:
(
-
9
,
-
1
)
C
’
:
(
-
7
,
-
1
)
D
’
:
(
-
7
,
1
)
Check by
counting squares
Draw the two shapes and label the vertices
A
D’
C’
B’
A’
D
C
B
“
DON’T
RUB ME
OFF”
S
h
a
p
e
1
A
(
-
9
,
6
)
B
:
(
-
9
,
2
)
C
:
(
-
5
,
2
)
D
:
(
-
5
,
6
)
S
h
a
p
e
2
A
’
:
(
-
9
,
1
)
B
’
:
(
-
9
,
-
1
)
C
’
:
(
-
7
,
-
1
)
D
’
:
(
-
7
,
1
)
C
h
e
c
k
b
y
l
o
o
k
i
n
g
a
t
v
e
c
t
o
r
s
Draw the two shapes and label the vertices
A
D’
C’
B’
A’
D
C
B
“
DON’T
RUB ME
OFF”
S
h
a
p
e
1
A
(
-
9
,
6
)
B
:
(
-
9
,
2
)
C
:
(
-
5
,
2
)
D
:
(
-
5
,
6
)
S
h
a
p
e
2
A
’
:
(
-
8
,
5
)
B
’
:
(
-
8
,
3
)
C
’
:
(
-
6
,
3
)
D
’
:
(
-
6
,
5
)
Where is the
centre of
enlargement?
Draw the two shapes and label the vertices
A
B’
C’
A’
D
C
B
D’
S
h
a
p
e
1
A
(
-
9
,
6
)
B
:
(
-
9
,
2
)
C
:
(
-
5
,
2
)
D
:
(
-
5
,
6
)
S
h
a
p
e
2
A
’
:
(
-
8
,
5
)
B
’
:
(
-
8
,
3
)
C
’
:
(
-
6
,
3
)
D
’
:
(
-
6
,
5
)
Check by
counting squares
Draw the two shapes and label the vertices
A
B’
C’
A’
D
C
B
D’
S
h
a
p
e
1
A
(
-
9
,
6
)
B
:
(
-
9
,
2
)
C
:
(
-
5
,
2
)
D
:
(
-
5
,
6
)
S
h
a
p
e
2
A
’
:
(
-
8
,
5
)
B
’
:
(
-
8
,
3
)
C
’
:
(
-
6
,
3
)
D
’
:
(
-
6
,
5
)
Check by looking
at vectors
Draw the two shapes and label the vertices
A
B’
C’
A’
D
C
B
D’
S
h
a
p
e
1
A
(
-
9
,
6
)
B
:
(
-
9
,
2
)
C
:
(
-
5
,
2
)
D
:
(
-
5
,
6
)
S
h
a
p
e
2
A
’
:
(
-
9
,
5
)
B
’
:
(
-
9
,
2
)
C
’
:
(
-
6
,
2
)
D
’
:
(
-
6
,
5
)
Where is the
centre of
enlargement?
Draw the two shapes and label the vertices
Notice how B = B’
This point is a fixed point and
is called an INVARIANT point.
A
D’
C’
A’
D
C
B
S
h
a
p
e
1
A
(
-
9
,
6
)
B
:
(
-
9
,
2
)
C
:
(
-
5
,
2
)
D
:
(
-
5
,
6
)
S
h
a
p
e
2
A
’
:
(
-
9
,
5
)
B
’
:
(
-
9
,
2
)
C
’
:
(
-
6
,
2
)
D
’
:
(
-
6
,
5
)
Check by
counting square
Draw the two shapes and label the vertices
Notice how B = B’
This point is a fixed point and
is called an INVARIANT point.
A
D’
C’
A’
D
C
B
T
i
t
l
e
:
E
n
l
a
r
g
e
m
e
n
t
To enlarge a 2D shape, two pieces of information are required:
•
Scale Factor
•
Centre of Enlargement
The scale factor describes how much bigger or smaller the enlarged image is to be.
The centre of enlargement determines where the enlarged image will be drawn.
Enlarged images are not the same size, therefore they are not congruent.
Invariant points are points that do not move when they are transformed.
D
e
s
c
r
i
b
e
t
h
e
t
r
a
n
s
f
o
r
m
a
t
i
o
n
o
f
A
t
o
B
A
B
A
B
W
o
r
k
e
d
E
x
a
m
p
l
e
Y
o
u
r
T
u
r
n
Enlargement, scale factor 2, (2, 4)
Enlargement, scale factor 3, (0, 3)
Enlargement, scale factor 2, (5, 3)
Enlargement, scale factor 3, (3, -4)
Enlargement, scale factor 1.5, (-5, 1)
Enlargement, scale factor 2.5, (-5, 5)
Enlargements increase the
size of a shape.
Always true,
sometimes true
or never true?
Using a fractional scale factor
will result in a smaller shape
Always true,
sometimes true
or never true?
For an enlargement to create
an invariant point the centre of
enlargement must
also be a vertex.
Always true,
sometimes true
or never true?
Dive into the world of shape enlargement and transformation through an intriguing visual journey. From plotting coordinates and labeling vertices to exploring scale factors and centers of enlargement, discover the fascinating properties of shapes and their transitions.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
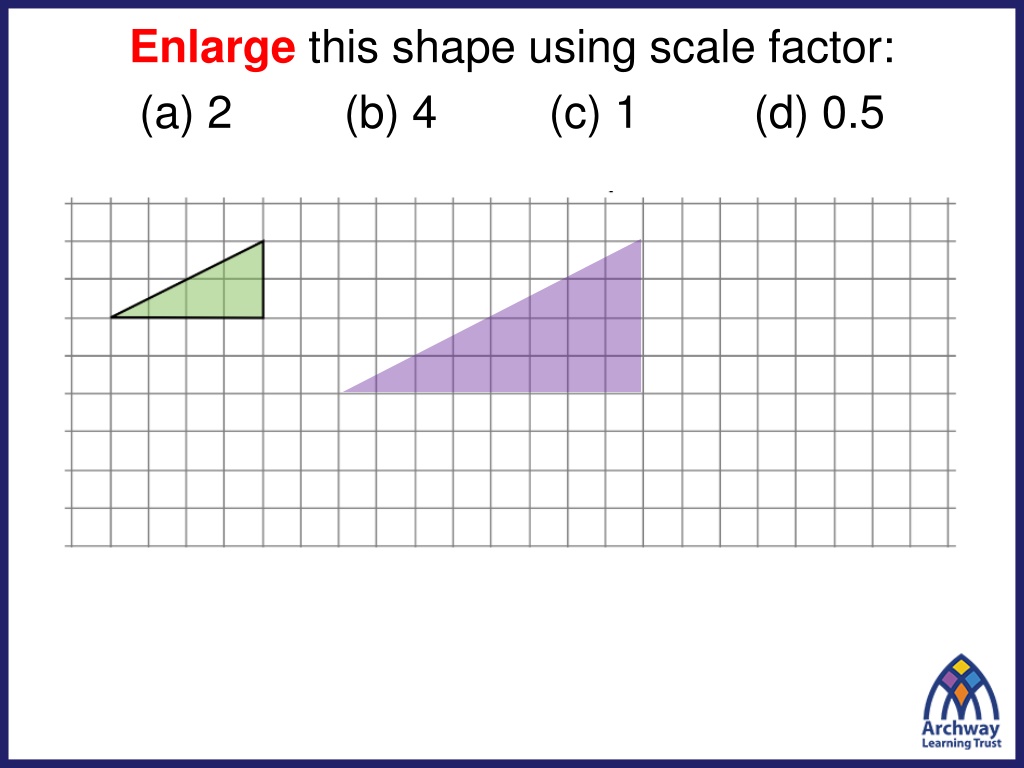
Enlarge this shape using scale factor: (a) 2 (b) 4 (c) 1 (d) 0.5
Enlarge this shape using scale factor: (a) 2 (b) 4 (c) 1 (d) 0.5
Plot the coordinates, join them up and label the vertices A D C B A:(6,6) B:(6,3) C:(12,3) D:(12,6) You should have a rectangle.
A D Can you include these words in your discussion? Scale Vertices Centre Angles Congruent A D C B C B What can we say about the new shape? A:(6,6) B:(6,3) C:(12,3) D:(12,6) Label the new vertices A , B , C and D
A D A D C B C B The centre of enlargement is (0,0)
A D DON T RUB ME OFF A D C B C B The centre of enlargement is (0,0)
A D DON T RUB ME OFF A D C B C B Notice that: Vector OA = ?? = 6 6 2 2 Vector OA = ?? =
A D What is the same? What is different? Can you include these words in your discussion? Scale Centre Vertices Intersect C B A D B C A:(6,6) B:(6,3) C:(12,3) D:(12,6) Label the new vertices A , B , C and D
A D Counting squares to check C B A D B C A:(6,6) B:(6,3) C:(12,3) D:(12,6) Label the new vertices A , B , C and D
A D C B A D B C ? Notice that: Vector XC = ?? = 15 6 5 2 Vector XC = ?? =
Draw the two shapes and label the vertices Shape 1 A(-9,6) B:(-9,2) C:(-5,2) D:(-5, 6) Shape 2 A : (-9,1) B :(-9,-1) C :(-7, -1) D :(-7, 1) A D Where is the centre of enlargement? DON T RUB ME OFF B C A D B C
Draw the two shapes and label the vertices Shape 1 A(-9,6) B:(-9,2) C:(-5,2) D:(-5, 6) Shape 2 A : (-9,1) B :(-9,-1) C :(-7, -1) D :(-7, 1) A D Check by counting squares DON T RUB ME OFF B C A D B C
Draw the two shapes and label the vertices Shape 1 A(-9,6) B:(-9,2) C:(-5,2) D:(-5, 6) Shape 2 A : (-9,1) B :(-9,-1) C :(-7, -1) D :(-7, 1) A D Check by looking at vectors DON T RUB ME OFF B C A D B C 0 6 0 3 Vector XB = ?? = Vector XB = ?? = ?
Draw the two shapes and label the vertices Shape 1 A(-9,6) B:(-9,2) C:(-5,2) D:(-5, 6) Shape 2 A :(-8,5) B :(-8,3) C :(-6,3) D :(-6,5) A D Where is the centre of enlargement? A D C B B C
Draw the two shapes and label the vertices Shape 1 A(-9,6) B:(-9,2) C:(-5,2) D:(-5, 6) Shape 2 A :(-8,5) B :(-8,3) C :(-6,3) D :(-6,5) A D Check by counting squares A D C B B C
Draw the two shapes and label the vertices Shape 1 A(-9,6) B:(-9,2) C:(-5,2) D:(-5, 6) Shape 2 A :(-8,5) B :(-8,3) C :(-6,3) D :(-6,5) A D Check by looking at vectors A D ? C B B C 2 2 1 1 Vector XA = ?? = Vector XA = ?? =
Draw the two shapes and label the vertices Shape 1 A(-9,6) B:(-9,2) C:(-5,2) D:(-5, 6) Shape 2 A :(-9,5) B :(-9,2) C :(-6,2) D :(-6,5) A D Where is the centre of enlargement? D A Notice how B = B C B C This point is a fixed point and is called an INVARIANT point.
Draw the two shapes and label the vertices Shape 1 A(-9,6) B:(-9,2) C:(-5,2) D:(-5, 6) Shape 2 A :(-9,5) B :(-9,2) C :(-6,2) D :(-6,5) A D Check by counting square D A Notice how B = B C B C This point is a fixed point and is called an INVARIANT point.
Title: Enlargement To enlarge a 2D shape, two pieces of information are required: Scale Factor Centre of Enlargement The scale factor describes how much bigger or smaller the enlarged image is to be. The centre of enlargement determines where the enlarged image will be drawn. Enlarged images are not the same size, therefore they are not congruent. Invariant points are points that do not move when they are transformed.
Describe the transformation of A to B Worked Example Your Turn B A A B This is an enlargement This is an enlargement Scale factor 2 Scale factor 0.5 Centre of enlargement is 1,3 Centre of enlargement is 0,3
Enlargement, scale factor 2, (2, 4) Enlargement, scale factor 3, (0, 3) Enlargement, scale factor 2, (5, 3) Enlargement, scale factor 3, (3, -4) Enlargement, scale factor 1.5, (-5, 1) Enlargement, scale factor 2.5, (-5, 5)
Always true, sometimes true or never true? Enlargements increase the size of a shape.
Always true, sometimes true or never true? Using a fractional scale factor will result in a smaller shape
Always true, sometimes true or never true? For an enlargement to create an invariant point the centre of enlargement must also be a vertex.
