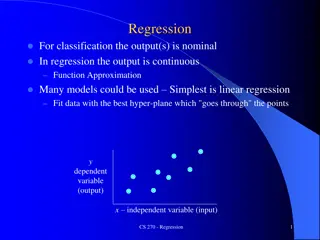
Regression Analysis in Social Sciences
Explore a practical regression example involving sales productivity evaluation in a software company. Learn how to draw scatterplots, estimate correlations, and determine significant relationships between sales calls and systems sold. Discover the process of predicting sales using regression analysis techniques.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Introduction to Statistics for the Social Sciences SBS200 - Lecture Section 001, Fall 2019 Social Sciences Room 100 10:00 - 10:50 Mondays, Wednesdays & Fridays. December 2
Schedule of readings Before next exam (December 9) OpenStax Chapters 1 13 (Chapter 12 is emphasized) Please read Chapters 17 and 18 Plous Chapter 17: Social Influences Chapter 18: Group Judgments and Decisions
Labs Continue this week
Regression Example Rory is an owner of a small software company and employs 10 sales staff. Rory send his staff all over the world consulting, selling and setting up his system. He wants to evaluate his staff in terms of who are the most (and least) productive sales people and also whether more sales calls actually result in more systems being sold. So, he simply measures the number of sales calls made by each sales person and how many systems they successfully sold.
Regression Example Ava 70 Emily Do more sales calls result in more sales made? Isabella 60 Emma 50 40 Step 1: Draw scatterplot Ethan 30 20 Joshua Step 2: Estimate r Jacob 10 Dependent Variable 0 0 1 2 3 4 Number of sales calls made Independent Variable
Regression Example Do more sales calls result in more sales made? Step 3: Calculate r Step 4: Is it a significant correlation?
Do more sales calls result in more sales made? Step 4: Is it a significant correlation? n = 10, df = 8 alpha = .05 Observed r is larger than critical r (0.71 > 0.632) therefore we reject the null hypothesis. Yes it is a significant correlation r (8) = 0.71; p < 0.05
Regression: Predicting sales Step 1: Draw prediction line r = 0.71 b = 11.579 (slope) a = 20.526 (intercept) Draw a regression line and regression equation
Regression: Predicting sales You should sell 32.105 systems Step 1: Predict sales for a certain number of sales calls Madison Step 2: State the regression equation Y = a + bx Y = 20.526 + 11.579x Joshua If make one sales call Step 3: Solve for some value of Y Y = 20.526 + 11.579(1) Y = 32.105 What should you expect from a salesperson who makes 1 calls? They should sell 32.105 systems If they sell more over performing If they sell fewer underperforming
Regression: Predicting sales You should sell 43.684 systems Step 1: Predict sales for a certain number of sales calls Isabella Step 2: State the regression equation Y = a + bx Y = 20.526 + 11.579x Jacob If make two sales call Step 3: Solve for some value of Y Y = 20.526 + 11.579(2) Y = 43.684 What should you expect from a salesperson who makes 2 calls? They should sell 43.68 systems If they sell more over performing If they sell fewer underperforming
Regression: Predicting sales You should sell 55.263 systems Ava Step 1: Predict sales for a certain number of sales calls Emma Step 2: State the regression equation Y = a + bx Y = 20.526 + 11.579x If make three sales call Step 3: Solve for some value of Y Y = 20.526 + 11.579(3) Y = 55.263 What should you expect from a salesperson who makes 3 calls? They should sell 55.263 systems If they sell more over performing If they sell fewer underperforming
Regression: Predicting sales You should sell 66.84 systems Step 1: Predict sales for a certain number of sales calls Emily Step 2: State the regression equation Y = a + bx Y = 20.526 + 11.579x If make four sales calls Step 3: Solve for some value of Y Y = 20.526 + 11.579(4) Y = 66.842 What should you expect from a salesperson who makes 4 calls? They should sell 66.84 systems If they sell more over performing If they sell fewer underperforming
Regression: Evaluating Staff Step 1: Compare expected sales levels to actual sales levels Ava Emma Isabella Emily Madison Joshua What should you expect from each salesperson Jacob They should sell x systems depending on sales calls If they sell more over performing If they sell fewer underperforming
Regression: Evaluating Staff Step 1: Compare expected sales levels to actual sales levels 70-55.3=14.7 Difference between expected Y and actual Y is called residual (it s a deviation score) Ava 14.7 How did Ava do? Ava sold 14.7 more than expected taking into account how many sales calls she made over performing
Regression: Evaluating Staff Step 1: Compare expected sales levels to actual sales levels 20-43.7=-23.7 Difference between expected Y and actual Y is called residual (it s a deviation score) Ava How did Jacob do? Jacob sold 23.684 fewer than expected taking into account how many sales calls he made under performing -23.7 Jacob
Regression: Evaluating Staff Step 1: Compare expected sales levels to actual sales levels Difference between expected Y and actual Y is called residual (it s a deviation score) Ava 14.7 Emma Isabella Emily Madison -23.7 Joshua Jacob
Regression: Evaluating Staff Step 1: Compare expected sales levels to actual sales levels Ava Emma Isabella Emily Madison Joshua What should you expect from each salesperson Jacob They should sell x systems depending on sales calls If they sell more over performing If they sell fewer underperforming
Regression: Evaluating Staff Step 1: Compare expected sales levels to actual sales levels Difference between expected Y and actual Y is called residual (it s a deviation score) Ava 14.7 Emma Isabella -6.8 Emily Madison -23.7 7.9 Joshua Jacob
Residual scores How do we find the average amount of error in our prediction Ava is 14.7 Jacob is -23.7 Emily is -6.8 Madison is 7.9 The average amount by which actual scores deviate on either side of the predicted score Step 1: Find error for each value (just the residuals) Y Y Difference between expected Y and actual Y is called residual (it s a deviation score) Step 2: Add up the residuals Big (Y Y ) = 0 problem Square the deviations 2 (Y Y ) x How would we find our average residual ? N Square root 2 (Y Y ) The green lines show how much error there is in our prediction line how much we are wrong in our predictions Divide by df n - 2
How do we find the average amount of error in our prediction Deviation scores Diallo is 0 Preston is 2 Mike is -4 Hunter is -2 Step 1: Find error for each value (just the residuals) Y Y Step 2: Find average Difference between expected Y and actual Y is called residual (it s a deviation score) (Y Y )2 n - 2 How would we find our average residual ? x N The green lines show how much error there is in our prediction line how much we are wrong in our predictions
Standard error of the estimate (line) = These would be helpful to know by heart please memorize these formula
How well does the prediction line predict the predicted variable when using the predictor variable? Standard error of the estimate (line) Standard error of the estimate: a measure of the average amount of predictive error the average amount that Y scores differ from Y scores a mean of the lengths of the green lines Slope doesn t give variability info Intercept doesn t give variability info Correlation r does give variability info Residuals do give variability info
A note about curvilinear relationships and patterns of the residuals How well does the prediction line predict the Ys from the Xs? Residuals Shorter green lines suggest better prediction smaller error Longer green lines suggest worse prediction larger error Why are green lines vertical? Remember, we are predicting the variable on the Y axis So, error would be how we are wrong about Y (vertical)
Does the regression line perfectly predict the dependent variable? No, we are wrong sometimes How can we estimate how much error we have? Difference between expected Y and actual Y is called residual (it s a deviation score) 14.7 The green lines show how much error there is in our prediction line how much we are wrong in our predictions -23.7 Perfect correlation = +1.00 or -1.00 Each variable perfectly predicts the other No variability in the scatterplot The dots approximate a straight line
Is the regression line better than just guessing the mean of the Y variable? How much does the information about the relationship actually help? Which minimizes error better? How much better does the regression line predict the observed results? r r2 2
What is r2? r2 = The proportion of the total variance in the predicted variable that is explained by its relationship with the predictor variable Examples If mother s and daughter s heights are correlated with an r = .8, then what amount (proportion or percentage) of variance of mother s height is accounted for by daughter s height? .64 because (.8)2 = .64
What is r2? r2 = The proportion of the total variance in the predicted variable that is explained by its relationship with the predictor variable Examples If mother s and daughter s heights are correlated with an r = .8, then what proportion of variance of mother s height is not accounted for by daughter s height? .36 because (1.0 - .64) = .36 or 36% because 100% - 64% = 36%
What is r2? r2 = The proportion of the total variance in the predicted variable that is explained by its relationship with the predictor variable Examples If ice cream sales and temperature are correlated with an r = .5, then what amount (proportion or percentage) of variance of ice cream sales is accounted for by temperature? .25 because (.5)2 = .25
What is r2? r2 = The proportion of the total variance in the predicted variable that is explained by its relationship with the predictor variable Examples If ice cream sales and temperature are correlated with an r = .5, then what amount (proportion or percentage) of variance of ice cream sales is not accounted for by temperature? .75 because (1.0 - .25) = .75 or 75% because 100% - 25% = 75%
Interpreting regression equation Prediction line Y = a+ b1X1 Cost will be about 95.06 The expected cost for dinner as predicted by the number of people Cost = 15.22 + 19.96 Persons Y-intercept People If People = 4 Slope If Persons = 4, what is the prediction for Cost ? Cost = 15.22 + 19.96 Persons Cost = 15.22 + 19.96 (4) Cost = 15.22 + 79.84 = 95.06 If Persons = 1, what is the prediction for Cost ? Cost = 15.22 + 19.96 Persons Cost = 15.22 + 19.96 (1) Cost = 15.22 + 19.96 = 35.18