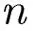Rainbow Cycles in Flip Graphs and Associahedra: Combinatorial Study
Exploring rainbow cycles and associated properties in the context of flip graphs and triangulations, this study delves into the diameter, realiability, automorphism group, and more of the associahedron. Motivated by binary reflected Gray codes, the research aims to find balanced Gray codes for various combinatorial classes.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Rainbow cycles in flip graphs Torsten M tze joint work with Stefan Felsner, Linda Kleist, Leon Sering (TU Berlin)
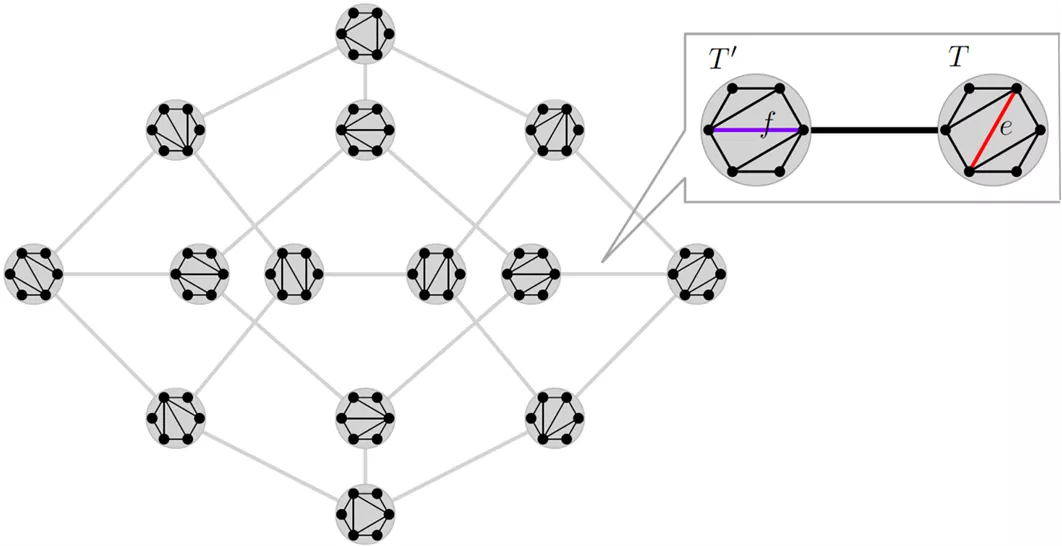
Flip graph of triangulations Define a graph Vertices = triangulations of a convex -gon Edges = flip a single edge of the triangulation sometimes called associahedron Example:
Properties of the associahedron What is the diameter of ? for sufficiently large for [Sleator, Tarjan, Thurston 88] , combinatorial proof [Pournin 14, Adv. Math.] Realizability as a convex polytope [Ceballos, Santos, Ziegler 15] Automorphism group, vertex-connectivity, chromatic number [Lee 89], [Hurtado, Noy 99], [Fabila-Monroy et al. 09] Hamiltonicity [Lucas 87], [Hurtado, Noy 99] Gray code for triangulations other Gray codes: - non-crossing perfect matchings [Hernando, Hurtado, Noy 02] - plane spanning trees [Aichholzer et al. 07] - non-crossing partitions, dissections of a convex polygon [Huemer et al. 09]
Rainbow cycles Hamilton cycle: cyclic listing of all combinatorial objects so that each object appears exactly once Dual problem: cyclic listing of some combinatorial objects so that each flip operation appears exactly once We call this a rainbow cycle -rainbow cycle = each edge appears times
Motivation binary reflected Gray code [Frank Gray 53] an algorithm to generate all bitstrings of length single bit in each step by flipping a 000 001 011 010 110 111 101 100 224 balanced Gray code: each bit is flipped many times (requires that [Tootill 53], [Bhat, Savage 96] this is a -rainbow cycle Our work: first step towards balanced Gray codes for other combinatorial classes (triangulations, matchings etc.) is a power of two)
Rainbow cycles Five settings triangulations of convex polygon spanning trees on arbitrary point sets non-crossing matchings permutations subsets
Triangulations Theorem: For , the graph Proof: Consider the following flip sequence has a 2-rainbow cycle. 3 2 1 Claim: - every edge appears twice: - uniqueness: can recognize and from intermediate triangulation is a 2-rainbow cycle
Matchings Theorem: For , the graph Assume that is even has no 1-rainbow cycle. Definition: Length of an edge := min. number of points on either side, divided by 2 Centered flip := sum of lengths of quadrilateral equals centered not centered Observation: A flip is centered iff quadrilateral contains origin.
Matchings Lemma: All flips along a rainbow cycle must be centered flips. Proof: same number of matching edges of each length Average length of edges that appear or disappear along a rainbow cycle = Average length of centered flip = Average length of non-centered flip <
Matchings Lemma: All flips along a rainbow cycle must be centered flips. Analyze subgraph of on centered flips to prove non-existence.
Subsets Graph : vertices = -element subsets of edges = subsets that differ in exchanging one element B A vertices edge colors Observation: For , a rainbow cycle is a Hamilton cycle.
Subsets Observation: For , a 1-rainbow cycle can be interpreted as an iterative 2-coloring of the edges of . blue = 2-subsets, red = exchanges
Subsets Theorem: For odd Hamilton cycle. Proof: and , the graph has a 1-rainbow cyclical right-shifts
Subsets Theorem: For odd Hamilton cycle. and , the graph has a rainbow 1 7 Proof: 6 2 starting element 1234567 1 2 3 1 2 3 3 1 2 3 5 4 rainbow block Lemma: Shifting a rainbow block yields a rainbow Hamilton cycle. Construct rainbow block directly.
Open problems -rainbow cycles for larger values of ? Other combinatorial classes? Matchings: prove non-existence of 1-rainbow cycle for even number of matching edges -subsets of : prove existence of 1-rainbow cycle for