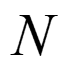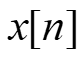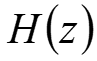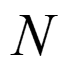Multirate Systems and their Applications
4
.
M
u
l
t
i
r
a
t
e
S
y
s
t
e
m
s
a
n
d
t
h
e
i
r
A
p
p
l
i
c
a
t
i
o
n
s
We compute here … and throw away most of them here!!!!
I
n
e
f
f
i
c
i
e
n
t
I
m
p
l
e
m
e
n
t
a
t
i
o
n
o
f
D
o
w
n
s
a
m
p
l
i
n
g
Most terms here are zero … and waste time to process them here!!!!
I
n
e
f
f
i
c
i
e
n
t
I
m
p
l
e
m
e
n
t
a
t
i
o
n
o
f
U
p
s
a
m
p
l
i
n
g
Same!!!
R
e
c
a
l
l
t
h
e
N
o
b
l
e
I
d
e
n
t
i
t
i
e
s
E
x
a
m
p
l
e
…
…
c
o
n
t
i
n
u
e
d
E
x
a
m
p
l
e
…
Same
…
c
o
n
t
i
n
u
e
d
In general: Polyphase Decomposition.
Take
N=
2:
G
e
n
e
r
a
l
F
i
l
t
e
r
:
P
o
l
y
p
h
a
s
e
D
e
c
o
m
p
o
s
i
t
i
o
n
with
Polyphase
Components
NOBLE
IDENTITY
POLYPHASE
D
o
w
n
s
a
m
p
l
i
n
g
u
s
i
n
g
P
o
l
y
p
h
a
s
e
D
e
c
o
m
p
o
s
i
t
i
o
n
This is a Serial to Parallel (a Buffer):
S/P
0 0 0 1 2 3 4 5 6 7
0 2 4 6
0 1 3 5
S
e
r
i
a
l
t
o
P
a
r
a
l
l
e
l
(
B
u
f
f
e
r
)
NOBLE IDENTITY
POLYPHASE
NOBLE
IDENTITY
U
p
s
a
m
p
l
i
n
g
u
s
i
n
g
P
o
l
y
p
h
a
s
e
D
e
c
o
m
p
o
s
i
t
i
o
n
This is a Parallel to Serial (an
Unbuffer):
P/S
0 2 4 6
0 1 3 5
0 0 0 1 2 3 4 5 6 7
P
a
r
a
l
l
e
l
t
o
S
e
r
i
a
l
(
U
n
b
u
f
f
e
r
o
r
I
n
t
e
r
l
a
c
e
r
)
Given any integer
N
:
Example: take
N=
3
G
e
n
e
r
a
l
P
o
l
y
p
h
a
s
e
D
e
c
o
m
p
o
s
i
t
i
o
n
POLYPHASE
A
p
p
l
y
t
o
D
o
w
n
s
a
m
p
l
i
n
g
…
…
a
p
p
l
y
N
o
b
l
e
I
d
e
n
t
i
t
y
S/P
1
2
3
4
5
1
2
6
3
4
5
6
Serial to Parallel (Buffer):
S
e
r
i
a
l
t
o
P
a
r
a
l
l
e
l
(
B
u
f
f
e
r
)
POLYPHASE
S
a
m
e
f
o
r
U
p
s
a
m
p
l
i
n
g
…
NOBLE IDENTITY
…
a
p
p
l
y
N
o
b
l
e
I
d
e
n
t
i
t
y
This is a Parallel to Serial (an
Unbuffer):
P/S
1
2
3
4
5
6
1
2
3
4
5
6
P
a
r
a
l
l
e
l
t
o
S
e
r
i
a
l
(
U
n
b
u
f
f
e
r
o
r
I
n
t
e
r
l
a
c
e
r
)
P
r
o
c
e
s
s
i
n
g
D
a
t
a
b
y
B
l
o
c
k
s
•
In most efficient implementations we process data by blocks, rather than one sample
at a time.
•
Real Time simulation and design software such as Simulink are designed to take
advantages of block processing for two purposes:
•
efficient computations, thus faster simulations;
•
efficient design.
“
S
a
m
p
l
e
B
a
s
e
d
”
a
n
d
“
F
r
a
m
e
B
a
s
e
d
”
S
i
g
n
a
l
s
Sample Based
:
time
They are MN
distinct
signals arranged in a matrix
Particular Case:
is like M distinct signals
“
S
a
m
p
l
e
B
a
s
e
d
”
a
n
d
“
F
r
a
m
e
B
a
s
e
d
”
S
i
g
n
a
l
s
Frame Based
:
They are N
distinct
signals, each one represented
as a sequence of frames of length M
Particular Case:
one signal as a sequence of
frames of length M
y0=
Frame based
y1=
Sample based
y2=y0=
Frame based
C
o
n
v
e
r
t
“
t
o
S
a
m
p
l
e
”
a
n
d
“
t
o
F
r
a
m
e
”
Example:
S
e
r
i
a
l
t
o
P
a
r
a
l
l
e
l
i
n
S
i
m
u
l
i
n
k
Serial to Parallel is implemented by the “Buffer” Simulink block in
Signal Processing Blcokset > Signal Management > Buffers:
S/P
Sample based
Frame based
E
x
a
m
p
l
e
o
f
D
o
w
n
s
a
m
p
l
i
n
g
P
a
r
a
l
l
e
l
t
o
S
e
r
i
a
l
i
n
S
i
m
u
l
i
n
k
Parallel to Serial is implemented by the “UnBuffer” Simulink block in
Signal Processing Blcokset > Signal Management > Buffers:
Frame based
Sample based
P/S
E
x
a
m
p
l
e
o
f
U
p
s
a
m
p
l
i
n
g
The implementation of downsampling and upsampling techniques in multirate systems, along with the use of Noble Identities for efficient processing. Dive into examples and polyphase decomposition for effective filtering. Learn about serial to parallel conversion using buffers in signal processing.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Inefficient Implementation of Downsampling [m y ] [n x ] ( ) z N H We compute here and throw away most of them here!!!! N
Inefficient Implementation of Upsampling [m y ] [n x ] ( ) z N H Most terms here are zero and waste time to process them here!!!! [m y ] ( ) z N H $$ $$
Recall the Noble Identities [n x ] [m y ] [n x ] Same!!! [m y ] ( ) z ( ) z N N N H H [n x ] [n x ] [m y ] [m y ] ( ) z ( ) z N N H N H
Example [n ] h = [ ] for 0 odd n h n = = + + + = 2 4 2 ( ) [ ] ] 0 [ h ] 2 [ h ] 4 [ h ... ( ) H z h n z z H z n [n x ] ( ) [m y ] 2z H 2 ( ) z = 5 . 1 + 5 . 1 2 . 1 + 2 2 4 6 0 . 2 H z z z [m y ] [n x ] ( ) z H 2 ( ) z = 5 . 1 + 5 . 1 2 . 1 + 1 2 3 0 . 2 H z z z
continued ( ) [n x ] [m y ] 2z H 2 [n ] h [m h ] m n ( ) z [n x ] [m y ] H 2
Example [n ] h Same [m y ] [n x ] ( ) 2z H 2 ( ) z = 5 . 1 + 5 . 1 2 . 1 + 2 2 4 6 0 . 2 H z z z [n x ] ( ) z [m y ] H 2 ( ) z = 5 . 1 + 5 . 1 2 . 1 + 1 2 3 0 . 2 H z z z
continued ( ) [n x ] [m y ] 2z H 2 [m h ] [n ] h m n [n x ] ( ) z [m y ] H 2
General Filter: Polyphase Decomposition In general: Polyphase Decomposition. Take N=2: ( ) z = + + + 2 4 ] 0 [ h ] 2 [ + ] 4 [ + ... + H h z h z ( ) + 1 2 5 ] 1 [ h ] 3 [ h ] 5 [ h ... z z z ( ) z ( ) z ( ) z = + 2 1 2 H H z H 0 1 m = 2 2 m ( ) 2 [ ] H z h m z Polyphase Components 0 with m = + 2 2 m ( ) 2 [ ] 1 H z h m z 1
Downsampling using Polyphase Decomposition [m y ] [n x ] ( ) z ( ) z 2 H1 2 H 1 z [m y ] [n x ] ( ) z 2 H0 POLYPHASE NOBLE IDENTITY ( ) 2 H 1z 1 z [n x ] [m y ] ( ) 2 2 H 0z
Serial to Parallel (Buffer) = 2 1[ ] x m [2 1] x m 1 z [n x ] = 2 0[ ] x m [2 ] x m This is a Serial to Parallel (a Buffer): [ ] 1m x 0 1 3 5 [n x ] S/P 0 0 0 1 2 3 4 5 6 7 2 0 2 4 6 [ ] 0m x = 0 n m = 0
Upsampling using Polyphase Decomposition [n x ] [m y ] ( ) z NOBLE IDENTITY 2 H ( ) z [n x ] [m y ] 2 H0 1 z ( ) z 2 H1 POLYPHASE [n x ] NOBLE IDENTITY ( ) [m y ] 2 2 H 0z 1 z ( ) 2 H 1z
Parallel to Serial (Unbuffer or Interlacer) [ ] y m 2 [ ] y 0n 1 z 2 [ ] 1n y This is a Parallel to Serial (an Unbuffer): 0[ ] y n [ ] y m 0 1 3 5 P/S 2 0 2 4 6 0 0 0 1 2 3 4 5 6 7 1[ ] y n n = 0 m = 0
General Polyphase Decomposition Given any integer N: + + 1 N ( ) z = n = k = = = + ( ) n Nk [ ] [ ] H h n z z h kN H z 0 N kz ( ) z ( ) z ( ) z ) 1 = + + + 1 ( N N N N ( ) ... H z H z H z H 0 1 1 N Example: take N=3 = 5 . 3 . + 2 . 4 6 . 0 + 4 . 1 2 . 0 7 . 0 + 1 2 3 4 5 6 7 ( ) 1 . 2 H z z z z z z z z = = = 2 . 4 + 3 3 6 ( ) 1 . 2 2 . 0 H z z z 0 + 3 3 6 ( ) 5 . 6 . 0 7 . 0 H z z z 1 3 3 ( ) 3 . 4 . 1 H z z 2
Apply to Downsampling ( ) z N [m y ] H [n x ] POLYPHASE ( ) N H z 1 N 1 z ( ) N H z 2 1 z ( ) N H z 1 1 z [n x ] [m y ] ( ) N N H z 0
apply Noble Identity N ( ) z H 1 N 1 z ( ) z N H 2 1 z ( ) z N H 1 1 z [n x ] [m y ] ( ) z N H 0
Serial to Parallel (Buffer) N = + 1[ ] m [( 1) 1] N x x m N 1 z N = 1[ ] x m [ 1] x mN 1 z [n x ] N = 0[ ] x m [ ] x mN Serial to Parallel (Buffer): 1[ ] m N x [n x ] 1 3 5 S/P 1 2 3 4 5 6 2 4 6 N [ ] 0m x = = 0 n n N m = 0
Same for Upsampling ( ) z N H [n x ] [m y ] POLYPHASE ( ) z [n x ] N [m y ] N H0 1 z ( ) z N H1 1 z ( ) z N H 1 N
apply Noble Identity ( ) z N [n x ] H [m y ] NOBLE IDENTITY [n x ] ( ) z [m y ] H0 N 1 z ( ) z H1 N 1 z ( ) z HN 1 N
Parallel to Serial (Unbuffer or Interlacer) N [ ] y m [ ] y 0n 1 z N 1[ ] n y N This is a Parallel to Serial (an Unbuffer): 0[ ] y n [ ] y m P/S 1 3 5 2 4 6 N 1 2 3 4 5 6 1[ ] n y N = n = m = m N 1 0 n = 0
Processing Data by Blocks In most efficient implementations we process data by blocks, rather than one sample at a time. Real Time simulation and design software such as Simulink are designed to take advantages of block processing for two purposes: efficient computations, thus faster simulations; efficient design.
Sample Based and Frame Based Signals N Sample Based: M M [ ] N time They are MN distinct signals arranged in a matrix Particular Case: M [ 1] 1[ ] x n [n x ] is like M distinct signals [ ] n x M
Sample Based and Frame Based Signals M Frame Based: 1[ ] x n M [ ] N [ ] N x n They are N distinct signals, each one represented as a sequence of frames of length M Particular Case: M [ 1] [n x ] one signal as a sequence of frames of length M M
Convert to Sample and to Frame Example: 5 y0= Frame based y1= Sample based 5 y2=y0= Frame based
Serial to Parallel in Simulink Serial to Parallel is implemented by the Buffer Simulink block in Signal Processing Blcokset > Signal Management > Buffers: 1[ ] m N x [n x ] S/P N [ ] 0m x N [ 1] 1 [ ] 1 Sample based Frame based Buffer
Example of Downsampling DF FIR DF FIR x1[m] x1[m] H1(z) H1(z) [2x1] [2x1] [2x1] [2x1] 1 1 1 1 x[n] x[n] x0[m] x0[m] y[m] y[m] Add Add Buffer Buffer DF FIR DF FIR H0(z) H0(z) 1[ ] x m x m 1[ ] ( ) z ( ) z 2 2 H1 H1 1 1 z z ( ) z ( ) z 2 2 H0 H0 [n x [n x ] ] [m y [m y ] ] 0[ ] x m x m 0[ ]
Parallel to Serial in Simulink Parallel to Serial is implemented by the UnBuffer Simulink block in Signal Processing Blcokset > Signal Management > Buffers: 0[ ] y n [ ] y m P/S N 1[ ] n y N N [ 1] 1 [ ] 1 Frame based Sample based Unbuffer
Example of Upsampling DF FIR DF FIR y0[n] y0[n] 1 1 H0(z) H0(z) To To 2 2 [2x1] [2x1] x[n] x[n] 1 1 Frame Frame 2 2 [2x1] [2x1] y[m] y[m] y1[n] y1[n] Frame Conversion Frame Conversion DF FIR DF FIR Unbuffer Unbuffer H1(z) H1(z) [ [ ] ] y y 0n 0n ( ) z ( ) z 2 2 [n x [n x ] ] [m y [m y ] ] H0 H0 1 1 z z ( ) z ( ) z 2 2 H1 H1 1[ ] y n y n 1[ ]
