Continuous-Time Markov Chains in Manufacturing Systems
Explore the world of Continuous-Time Markov Chains (CTMC) in manufacturing systems through the lens of stochastic processes and performance analysis. Learn about basic definitions, characteristics, and behaviors of CTMC, including homogeneous CTMC and Poisson arrivals. Gain insights into the memoryless property and steady-state performances of CTMC models.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Chapter 5 Continuous time Markov Chains Learning objectives : Introduce continuous time Markov Chain Model manufacturing systems using Markov Chain Able to evaluate the steady-state performances Textbook : C. Cassandras and S. Lafortune, Introduction to Discrete Event Systems, Springer, 2007 1
Plan Basic definitions of continuous time Markov chains Characteristics of CTMC Performance analysis of CTMC Poisson process Approximation of general distributions by phase type distribution 2
Basic definitions of continuous time Markov chains 3
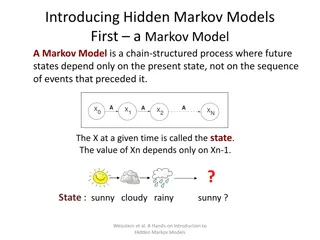
Continuous Time Markov Chain (CTMC) Stochastic process Continuous event Discrete events Continuous time A CTMC is a continuous time and memoriless discrete event stochastic process. Discrete time Memoryless 4
Continuous Time Markov Chain (CTMC) Definition : a stochastic process with discrete state space and continuous time {X(t), t > 0} is a continuous time Markov Chain (CTMC) iff P[X(t+s)= j X(u), 0 u t] = P[X(t+s)= j X(t)], t, s, j Memoryless: In a CTMC, the past history impacts on the future evolution of the system via the current state of the system 5
Continuous Time Markov Chain (CTMC) Exponential service time Poisson Arrivals N(t) : number of customers at time t Customer Arrivals Customer departures 6
Homogenuous CTMC Definition : A CTMC {X(t), t > 0} is homogeneous iff P[X(t+s)= j X(t) = i] = P[X(s)= j X(0) = i] = pij(s) Homogeneous memoryless: In reliability, we only say "a machine that does not fail at age t is as good as new" Only homogeneous CTMC will be considered in this chapter. 7
Behavior of a CTMC X(t) Two major components: Ti = sojourn time in state i (random variable) pij = probability of moving to state j when leaving state i 9
Sojourn time in a state Let Tibe the random variable corresponding to the time spent in state i The memoryless property of the homogenuous CTMC implies P T + = , , t x T t P T x t x i i i The exponential distribution is the only continuous probability distribution having this property. In an CTMC, the sojourn time in any state is exponentially distributed. 10
Exponential distribution Let T be a continuous random variable with an exponential distribution of parameter Distribution Function (figure) : FT(t) = P{T t} t 1 0, , 0 0 e t t ( ) t = F T Probability density function : fT(t) = dFT(t)/dt t , 0 0 e t t ( ) t = f T 0, Mean : E[T] = 1/ Standard deviation: [T] = 1/ Coeficient of variation: Cv(T) = [T]/ E[T] = 1 Parameter often corresponds to some event rate (failure rate, repair rate, production rate, ...) 11
Exponential distribution Memoryless : + P t T t t s + = P T t s T t P T ( ) t s + t e e = = = s 1 e P T s t e For a machine with exponentially distributed lifetime, we say that it is "as good as new" if it is not failed. The remaining lifetime of an used but UP machine has the same distribution as a new machine. 12
Transition probability When a CTMC leaves state i, it jumps to state j with probability pij. This probability is: independent of time as the CTMC is homogeneous independent of sojourn time Ti as the process is markovian (memoryless) 13
1st characterization of a CTMC An CTMC is fully characterized by the following parameters: { i}i E with i as the parameter of the exponential distribution of sojourn time Ti {pij}i j , with pij as the transition probability from i to j when leaving state i 14
Classification of a CTMC Each CTMC is associated an underlying DTMC by neglecting sojourn times. A state i of a CTMC is said transient (resp. recurrent, absorbing) if it is transient (resp. recurrent, absorbing) in the underlying DTCM A CTMC is irreducible if its underlying DTMC is irreducible. Remark: the concept of periodicity is not relevant. 15
2nd characterization of a CTMC Each state activates several potential events leading to different transitions. A CTMC travels from state i to state j in Tijtime, an exponentially distributed random variable with parameter ij. iis called transition rate from i to j. 16
Equivalence of the two representation Let Ti= MINj{Tij} pij= P{Tij= Ti} Result to prove: Ti= EXP( ij), pijis independent of Ti Moment generating function MX(u) = E[exp(uX)] 17
Probability distribution State probability i(t) = P{X(t) = i} state probability vector, also called probability distribution (t) = ( 1(t), 2(t), ...) 19
Transient analysis By conditionning on X(t), With 20
Transient analysis It can be shown, Letting dt go to 0, 21
Infinitesimal generator Let The matrix Q = [qij] is called infinitesimal generator of the CTMC As a ressult, 22
Transient state + ( ) Laplace transforms of function f(t) ( ) ( ) ( ) t Q s dt s sI Q = = st ( ) F s e f t dt 0 d t ( ) 0 ( ) s Q = = s ( ) ( )( 0 ) 1 Example + + 1 s 1 ( ) s ( ) 0 = + 0 1 1 + + + + 1 s ( ) t ( ) 0 ( ) + t = + e 1 1 23
Transient state = 0.1, = 0.5 = 0.9, = 0.8 1 1 0.9 0.9 0.8 0.8 0.7 0.7 p1(t) p0(t) 0.6 0.6 0.5 0.5 0.4 0.4 0.3 0.3 p1(t) p0(t) 0.2 0.2 0.1 0.1 0 0 0 5 10 15 20 25 0 5 10 15 20 25 = 0.01, = 0.05 = 0.09, = 0.08 1 1 0.9 0.9 0.8 0.8 0.7 0.7 0.6 0.6 0.5 p1(t) p0(t) 0.5 0.4 0.4 0.3 0.3 0.2 0.2 p1(t) p0(t) 0.1 0.1 0 0 0 5 10 15 20 25 0 5 10 15 20 25 24
Transient state: numerical computation max i 1. Uniformization with rate ij j 0 1 2. Derived the embeded discrete-time Markov Chain 1 1 , ii ij ij ij j p p = 3. Determine distribution Dof (2) 4. Determine distribution ( ) ! n n = 0 1 ( ) n n n t t 1 N ( ) t ( ) t = = + t D n t D n e e N ! = = 0 0 n ( ) n ( ) n n n t t 1 N ( ) t = t t 1 e e N ! ! = 0 n N n ( ) N N N t 1 te N ( ) t (Stirling's approximation of !) N N ! 2 N 25
Transient state: numerical computation Example: = 0.1, = 1, Uniformization with rate = 1 (0) = 1 ( ) 1 ! n n = t p0 0,5 0,61540891 1 0,39351916 2 0,19163922 5 0,09462431 10 0,0909242 100 0,09090902 200 0,09090902 0 1 n t 1 N ( ) t 6 t 10 e N 0 p1 0,38459102 0,60648073 0,80836058 0,90537535 0,90907503 0,90909018 0,9090902 N-1 7 9 12 19 28 151 271 26
Steady state distribution of a CTMC Thereom: For an irreducible CTMC with postive recurrent states, the probability distribution converges to a vector of stationary probabilities ( 1, 2, ...) that is independent of the initial distribution (0). Further it is the unique solution of the following equation system: normalization equation flow balance equation or equilibrium eq 27
Flow balance equation The balance equation equivalent to : i j j ji = i j i ij Associate to each transition (i,j) a probability flow : i ij i j j ji: total flow into state i i j i ij: total flow out of state i Interpretation : Total flow in = Total flow out 28
Flow balance equation of set of states Let E1be a subset of states Flow balance equation : Total flow into E1= Total flow out of E1 29
A manufaturing system Consider a machine which can be either UP or DOWN. The state of the machine is checked continuously. The average time to failure of an UP machine is 10 days. The average time for repair of a DOWN machine is 1.5 days. Determine the conditions for the state of the machine {X(t)} to be a Markov chain. Draw the Markov chain model. Find the transient distribution by starting from state UP and DOWN. Check whether the Markov chain is recurrent. Determine the steady state distribution. Determine the availability of the machine. 30
Poisson process A Poisson process is a stochastic process N(t) such that N(0) = 0 N(t) increments by +1 after a time T random distributed according to an exponential distribution of parameter . An arrival process is said Poisson if the inter-arrival times are exponentially distributed. 32
Properties of Poisson process A Poisson process is a CTMC N(t) has a Poisson distribution with parameter t 33
Properties of Poisson process A Poisson process is a CTMC P{N(t+dt) = k+1 | N(t) = k} = dt + o(dt) Probability of 0 arrival in dt P{N(t+dt) = k | N(t) = k} = 1- dt + o(dt) Probability of more than one arrival in dt P{N(t+dt) > k+1 | N(t) = k} = o(dt) 34
Properties of Poisson process The superposition of n Poisson process of parameter iis a Poisson process of parameter i Assume that a Poisson process is split into n processes with probabilities pi. These n process are independent Poisson process with parameter pi 35
Definition Consider a population of individuals Let N(t) be the size of the population with N(t) = 0, 1, 2, ... When N(t) = n, births arrive at according to a Poisson pocess of birth rate n > 0 Deaths arrive also according to a Poisson process of death rate n > 0. 37
Key issues Graphic representation of the Markov chain Relation with the Poisson process (also called pure birth process) Condition for existence of steady state distribution ... ... n = 0 1 n S = 1 n 1 Sufficient condition (larger death rate than birth rate) + n 1, * n n 1 n Steady state distribution n 38
Approximation of general distributions by phase type distribution 39
Erlang distribution Ek( ) Ek : k-stage Erlang distribution with parameter X = X1+ + Xk ; Xi = EXP ( ) E[X] = k/ Var[X] = k/ 2 cvX = X / E[X] = k 1 k k x x k e ( ) = ; ; f x k ( ) 1 ! Identical phases 40
Hyper-exponential or mixture of exponential distribution X = EXP( 1), avec proba 1 = EXP( 2), avec proba 2 = EXP( n), avec proba n E[X] = 1/ 1 + 2/ 2 ... + n/ n E[X2] = 2 1/ 12 + 2 2/ 22 ... + 2 n/ n2 Two moment matching of mean m and variance 2 with X = EXP( 1), = 0, : E[X]= m & Var(X) = 2, iff 2 m2 avec proba avec proba 1- 41
Serial phase distribution X = X0 +X1+ + Xk ; X0 = EXP ( 0), Xi = EXP ( ) E X = + 1 1 k 0 + X = 2 X 2 2 2 k E 0 1 cv X Two moment matching of mean m and variance 2 with ( ( 0 ) ): E[X]= m & Var(X) = 2, iff (k+1)-1 2/m2 1 Not ident phases 42
Phase-type distribution A probability distribution that results from a system of one or more inter-related Poisson process occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process. Phase-type distribution = time until the absorption of a CTMC one absorbing state and m transient states. Each of the states of the Markov process represents one of the phases. Phase-type distributions can be used to approximate any positive valued distribution. 43
Definition A CTMC with m+1 states, where m 1, such that the states 1,...,m are transient states and state m+1 is an absorbing state. An initial probability of starting in any of the m+1 phases given by the probability vector ( , m+1). The continuous phase-type distribution is the distribution of time from the above process's starting until absorption in the absorbing state. This process can be written in the form of a transition rate matrix, = 0 0 S S Q 0 where S is an m m matrix and S0 = -S 1 with 1 represents an m 1 vector with every element being 1 44
Characterization Time X until the absorbing state is phase-type distributed PH( ,S). The distribution function of X is given by, F(x) = 1 - exp(Sx)1, and the density function, f(x) = exp(Sx)S0, for all x > 0. Mean: E[Xn] = (-1)n n! S-n1 45
Serial phase distribution = = sum of independent exponentially distributed r.v. , i i i X X EXP E Y m = Y Y ( ) = = i = 2 Y 2 i 2 i 2 m E Y 1 cv Y To be proved: two-moment matching of a r.v. X with n-stage serial phase distribution iff 1 X n CV Proof by induction 1 2 Not ident phases n 46
Hyper-exponential or mixture of exponential distribution X = 1X1 + 2X2 ... + nXn where P(Ii = 1) = i, P(Ii = 0) = 1- i 1 + 2 ... + n = 1, Xi = EXP( i) By Jensen s inequality, 2 X E[X] = 1/ 1 + 2/ 2 ... + n/ n E[X2] = 2 1/ 12 + 2 2/ 22 ... + 2 n/ n2 2 i 2 X 2 E i i i i i 1 cv X Two moment matching of a random variable X with mean m and variance 2 m2 (???) X = 1X1 + 2X2where X1 = EXP( 1), X2 = 0 47
Coxian distribution Coxian distribution can be used to approximate any distribution. Phases not necessarily identical p1 p2 pn-1 n 1 1-p1 1-p2 Theorem: There exists an exact two moment matching with n-stage Coxian distribution for a random variable X iff 2 X 1 where n = 2 X 2 X Proof by induction cv cv X 2 E 48
Coxian distribution p1=p p2=1 pn-1=1 2 1 1-p1 1-p2 1 n n ( ) E X = = = 2 X 1 2 X 1 1 , , p cv cv E X 1 2 1 n Also two-moment matching with n-stage serial distribution. 49
A manufaturing system Consider a machine which can be either UP or DOWN. The state of the machine is checked continuously. The average time to failure of an UP machine is 10 days. The average time for repair of a DOWN machine is 1.5 days. Assumed that UP time = E2and DOWN time = E3. Draw the Markov chain model. Homework: Solve the same problem with Coxian distribution with the same means but 2 2 0.6, UP DOWN cv cv = = 1.5 50