Geometric Reasoning for Year 8 Students
Explore geometric reasoning with Dr. J. Frost's lessons on identifying 2D polygons, properties of quadrilaterals, interior angles of shapes, and the sum of interior angles in polygons. Test your understanding with exercises and learn how to calculate angles in different polygons.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Year 8: Geometric Reasoning Dr J Frost (jfrost@tiffin.kingston.sch.uk) Objectives: Be able to reason about sides and angles, and find interior/exterior angles of polygons. Last modified: 12th April 2014
STARTER: Identifying 2D polygons ? A polygon is a 2D shape with straight sides. Sides: 3 Triangle Equilateral ? Isosceles ? Scalene ? Square ? Rectangle ? Rhombus ? 4 Quadrilateral ? Parallelogram ? Trapezium ? Kite ? Arrowhead ? 5 6 7 ? ? ? Pentagon 8 9 10 12 20 ? ? ? Dodecagon ? ? Octagon Hexagon Nonagon Icosagon Heptagon Decagon
Properties of quadrilaterals Diagonals always equal? Diagonals perpen- dicular? Lines of symmetry Num pairs of parallel sides Shape Name ? ? ? ? Square 4 2 Yes Yes ? ? ? ? Rectangle 2 2 Yes No ? ? ? ? Kite 1 0 No Yes ? ? ? ? Rhombus 2 2 No Yes ? ? ? ? Parallelogram 0 2 No No ? ? ? ? Arrowhead 1 0 No Yes
RECAP: Interior angles of quadrilateral The interior angles of a quadrilateral add up to 360 . ? Parallelogram 1 2 y 100 x x 50 x = 130 ? x = 100 y = 80 ? ? 3 4 Trapezium Kite x x = 120 ? x 55 95 60 x = 105 ?
Sum of interior angles n = 3 n = 4 Total of interior angles = 360 Total of interior angles = 180 Can you guess what the angles add up to in a pentagon? How would you prove it?
Sum of interior angles Click to Bromanimate We can cut a pentagon into three triangles. The sum of the interior angles of the triangles is: 3 x 180 = 540 For an n-sided shape, the sum of the interior angles is: 180(n-2) ?
Test Your Understanding A regular decagon (10 sides). 160 x x 80 130 120 x = 140 ? x = 144 ? 120 x 40 100 x = 240 ? 40
Exercise 1 1a b c ? x = 75 ? x = 25 d e f x = 222 ? x = 309 ?
Exercise 1 g h i x = 120 x = 252 ? ? x = 54 ? The total of the interior angles of a polygon is . How many sides does it have? 2 ? The interior angle of a regular polygon is . How many sides does it have? 1 ?
Exercise 1 If a n-sided polygon has exactly 3 obtuse angles (i.e. 90 < < 180 ), then determine the possible values of (Hint: determine the possible range for the sum of the interior angles, and use these inequalities to solve). 2 ?
Interior Angles An exterior angle of a polygon is an angle between the line extended from one side, and an adjacent side. Which of these are exterior angles of the polygon? NO ? YES ? ? NO
Interior Angles To defeat Kim Jon Il, Matt Damon must encircle his pentagonal palace. What angle does Matt Damon turn in total? 360 ? The sum of the exterior angles of any polygon is 360 . Click to Start Damonimation
Interior Angles If the pentagon is regular, then all the exterior angles are clearly the same. Therefore: Exterior angle of pentagon = 360 / 5 = 72 ? Interior angle of pentagon = 180 72 = 108 ?
Angles in Regular Polygons Num Sides Name of Regular Polygon Exterior Angle Interior Angle ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 3 Triangle 120 60 4 Quadrilateral 90 90 5 Pentagon 72 108 6 Hexagon 60 120 7 Heptagon 51.4 128.6 8 Octagon 45 135 9 Nonagon 40 140 10 Decagon 36 144 Bonus Question: What is the largest number of sides a shape can have such that its interior angle is an integer? 360 sides. The interior angle will be 179 . ?
Test Your Understanding GCSE question The diagram shows a regular hexagon and a regular octagon. Calculate the size of the angle marked x. You must show all your working. x = 105 ?
GCSE Question Hint: Fill in what angles you do know. You can work out what the interior angle of Tile A will be. Question: The pattern is made from two types of tiles, tile A and tile B. Both tile A and tile B are regular polygons. Work out the number of sides tile A has. Sides = 12?
Test Your Understanding Q1 Q2 50 85 75 a 80 80 80 c a = 110 ? c = 70 ? Q3 Q4 What is the exterior angle of a 180-sided regular polygon? 360 180 = 2 ? The interior angle of a regular polygon is 165. How many sides does it have? Interior angle = 180 165 = 15 n = 360 15 = 24 ? Alternative method: Total interior angle = 165n Then solve 180(n 2) = 165n
Exercise 2 Q3 Determine how many sides a regular polygon with the following exterior angle would have: 30 45 12 9 Q1 ? ? 12 sides 8 sides 30 sides 40 sides ? ? The diagram shows a regular hexagon and a regular octagon. Calculate the size of the angle marked. You must show all your working. Interior angle of hexagon: 180 (360/6) = 120 Interior angle of octagon: 180 (360/8) = 135 x = 360 120 135 = 105 ? Determine how many sides a regular polygon with the following interior angle would have: 156 162 144 175 Q2 Q4 ? ? The pattern is made from two types of tiles, tile A and tile B. Both tile A and tile B are regular polygons. Work out the number of sides tile A has. Interior angle of A = (360 60)/2 = 150 Exterior angle = 30 Sides = 360/30 = 12 15 sides 20 sides 10 sides 72 sides ? ? ?
Exercise 2 A regular polygon is surrounded by squares and regular hexagons, alternating between the two. How many sides does this shape have? Find all regular polygons which tessellate (when restricted only to one type of polygon). Q5 Q6 ? Equilateral triangle, square, hexagon. By thinking about interior angles, prove that the regular polygons you identified above are the only regular polygons which tessellate. Method 1: The possible exterior angles of a regular polygons are the factors of 360 less than 180: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 This gives interior angles of 179, 178, ..., 140, 135, 120, 108, 90, 60. To tessellate, the interior angle has to divide 360. Only 120, 90 and 60 does. This corresponds to a hexagon, square and equilateral triangle. Interior angle = 360 90 120 = 150 n = 360 / 30 = 12 sides ? ? Method 2: 360 divided by the interior angle must give a whole number, in order for the regular polygon to tessellate. Interior angle is 180 (360/n), so 360 / (180 (360/n)) = k for some constant k. Simplifying this gives kn 2k 2n = 0 This factorises to (k 2)(n 2) = 4 This only numbers which multiply to give 4 are 1 x 4 or 2 x 2 or 4 x 1. This n = 6, 4 or 3 in each case.
TEST YOUR UNDERSTANDING Vote with your diaries! A B C D
What is the total exterior angle of a polygon in terms of the number of sides n? 360 n 360 360n 180(n-2)
What is the total interior angle of a 20 sided polygon? 360 3600 3240 6480
The interior angle of a polygon is 178. How many sides does it have? 20 40 90 180
What is the interior angle of a 90 sided regular polygon? 172 176 178 179
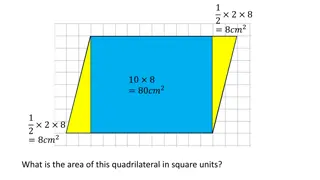
Determine the angle . 61 29 105 120 215 223 225 235