Exponents and Logarithms in Mathematics
An exponent is a shorthand notation for repeated multiplication, while logarithms are the opposite of exponents, dealing with unknown exponents in equations. This module explores these concepts along with basic algebraic operations, factorization, and fractions, providing a foundation for understanding advanced mathematical principles.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Mathematics N1
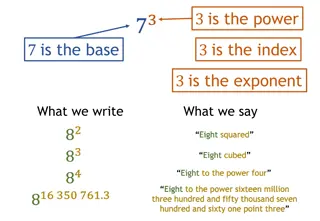
Module 1: Exponents and logarithms EXPONENTS (INDICES) An exponent, also referred to as an index, is more or less a shorthand notation for multiplying the same number by itself several times, for example: 2 2 2 = 23= 8 In this example, the 3 is the exponent. www.futuremanagers.com
Module 1: Exponents and logarithms (continued) LOGARITHMS Logarithms are the opposite of exponentials. The logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. Therefore a logarithm is an unknown exponent that will be determined. For example: The logarithm of 100 to base 10 is 2, written as ???10100 = 2 www.futuremanagers.com
Module 2: The four basic algebraic operations THE SCIENTIFIC POCKET CALCULATOR The scientific calculator pays attention to the priority of a maths sequences, therefore it automatically evaluates an answer according to BODMAS . There are several functions that a scientific calculator can perform: Inverse or reciprocal; Squares and number powers; Roots; and Fractions. www.futuremanagers.com
Module 2: The four basic algebraic operations (continued) THE FOUR BASIC ALGEBRAIC OPERATIONS The four basic algebraic operations are: Additional (only like terms can be added); Subtraction (only like terms can be subtracted); Multiplication (all terms can be multiplied); and Division (all terms can be divided). When calculating an equation, BODMAS is important to consider. www.futuremanagers.com
Module 3: Factorisation and fractions FACTORISATION, HCF AND LCM Writing a mathematical statement as a product of its factors is called factorisation. The highest common factor (HCF) of two or more numbers is the common factor of all those numbers with the greatest value. The first step in factorisation is to take out the HCF. The lowest common multiple (LCM) of two or more numbers is the smallest possible number into which all the numbers will divide exactly. www.futuremanagers.com
Module 3: Factorisation and fractions (continued) ALGEBRAIC FUNCTIONS Fractions can be simplified by dividing the numerator and the denominator by the same factor. When operating the algebraic functions with fractions, there are certain rules to consider. For example, fractions can only be added or subtracted if they share the same denominator. www.futuremanagers.com
Module 4: Equations, word problems and manipulation of technical formulae LINEAR EQUATIONS An equation is a mathematical statement that includes an = sign. A linear equation is an equation in which the highest variable you are solving for is equalled to 1. A linear equation cannot have more than one unique solution (often called root) for ?, for example: If 2? + 1 = 9 , the solution that would make the statement true is if ? = 4. www.futuremanagers.com
Module 4: Equations, word problems and manipulation of technical formulae (continued) WORD PROBLEMS When an answer is needed to a mathematical problem that is described in words as well as numbers, it is called a word problem. You find the solution by setting up an equation that represents the problem, and then solve it. www.futuremanagers.com
Module 4: Equations, word problems and manipulation of technical formulae (continued) MANIPULATION OF TECHNICAL FORMULAE Manipulation of technical formula is often described as changing the subject of the formula. www.futuremanagers.com
Module 5: Algebraic graphs COORDINATES ON A CARTESIAN PLANE The Cartesian plane is the two-dimensional space mapped out by the x-and y-axes. The vertical axis is the y-axis. The horizontal axis is the x-axis. The x- and y-axes divide the Cartesian plane in four quadrants. (x; y) is called an ordered number pair or coordinates www.futuremanagers.com
Module 5: Algebraic graphs (continued) FUNCTION NOTATION A linear equation of the form ? = ?? + ? can be written in the form ? ? = ?? + ? and a rectangular hyperbola in the form ?? = ? or ? + ?? can be written in the form ? ? = ??. ? ? = ?? + ? and ? ? = ?? is also called function notation. www.futuremanagers.com
Module 5: Algebraic graphs (continued) LINEAR GRAPHS (STRAIGHT-LINE GRAPHS) A linear equation is an equation with an expression of degree 1. The degree of an expression is given by the highest value found among the degrees of all the terms in the expression. Such a linear equation can be represented graphically by a straight line, for example: ? = 3? + 2 www.futuremanagers.com
Module 5: Algebraic graphs (continued) INTERCEPTS AND GRADIENTS OF STRAIGHT-LINE GRAPHS The gradient (referred to as m) of a straight line is the measure of its slope relative to the x-axis. www.futuremanagers.com
Module 5: Algebraic graphs (continued) RECTANGULAR HYPERBOLA Characteristics of a rectangular hyperbola: There are no x- or y-intercepts The graph strives towards the x- and y-axes but never touches or cuts the axes, ? 0 and ? = 0. The hyperbola consists of two separate curves: www.futuremanagers.com
Module 6: Triangles PROPERTIES OF TRIANGLES There are many different types of triangles: Equilateral triangle All sides are equal and all angles are equal to 60 ; Isosceles triangle Two sides are equal with base angles also equal; Scalene triangle No sides or angles are equal; Acute-angled triangle All three angles are smaller than 90 ; Obtuse-angle triangle One angle is greater than 90 ; and Right-angled triangle One angle is equal to 90 . www.futuremanagers.com
Module 6: Triangles (continued) PYTHAGORAS THEOREM Pythagoras theorem states the following: The area of a square built upon the hypotenuse of a right triangle is equal to the sum of the areas of the squares upon the remaining sides. This means if you have a right-angled triangle ABC with ? = 90 , then ?2 + ?2 = ?2. www.futuremanagers.com
Module 7: Trigonometry TRIGONOMETRY Trigonometry is the study of triangles, the relationship between the lengths of their sides, and the angles between those sides, including the behaviour of certain wave functions. www.futuremanagers.com
Module 8: Mensuration and percentages MENSURATION Mensuration means to establish the size, amount, quantity or extent of something by comparing it with something of standard size, or with an item marked off in standard units. For example, 1,000m = 1km. www.futuremanagers.com
Module 8: Mensuration and percentages (continued) PERCENTAGES Per cent means divided by 100. For example, if you are talking about 37%, you are saying 37 100. Percentages are used in everyday contexts, such as in tax and discounts. www.futuremanagers.com