Exploring Symmetric Chains and Hamilton Cycles in Graph Theory
Delve into the study of symmetric chains, Hamilton cycles, and Boolean lattices in graph theory. Discover the relationships between chain decompositions, Boolean lattices, and edge-disjoint symmetric chain decompositions, exploring construction methods and properties such as orthogonality. Uncover the significance of these concepts in various applications within the realm of posets and combinatorial mathematics.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
On symmetric chains and Hamilton cycles Torsten M tze (based on joint work with Karl D ubel, Sven J ger, Petr Gregor, Joe Sawada, Manfred Scheucher, and Kaja Wille)
The Boolean lattice consider all subsets of ordered by inclusion a fundamental and widely studied poset called -cube -th level := all subsets of cardinality its size is 4-cube
The Boolean lattice consider all subsets of ordered by inclusion a fundamental and widely studied poset called -cube -th level := all subsets of cardinality its size is odd even middle level(s)
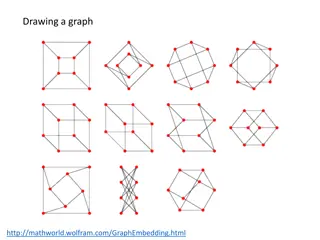
Chain decompositions Theorem [Sperner 28]: The width (=size of a maximum antichain) of the -cube is given by the size of its middle level(s) . Theorem [Dilworth 50]: Any poset into can be decomposed many chains. 4-cube chain decomposition
Symmetric chain decompositions useful for applications: symmetric chains, i.e., if a chain starts at level , then it ends at level known constructions of SCDs for the -cube due to [De Bruijn, van Ebbenhorst Tengbergen, Kruiswijk 51], [Lewin 72], [Aigner 73], [White and Williamson 77], [Greene, Kleitman 76] all constructions yield the same SCD not symmetric . 4-cube symmetric chain decomposition (SCD)
Parenthesis matching useful for applications: symmetric chains, i.e., if a chain starts at level , then it ends at level known constructions of SCDs for the -cube due to [De Bruijn, van Ebbenhorst Tengbergen, Kruiswijk 51], [Lewin 72], [Aigner 73], [White and Williamson 77], [Greene, Kleitman 76] all constructions yield the same SCD . parenthesis matching description by [Greene, Kleitman 76] 1001110111 1001110110 1001110100 1001100100 0001100100
Edge-disjoint and orthogonal SCDs Question: Are there other constructions? Definition: Two SCDs are edge-disjoint, if they do not share any edges Definition: Two SCDs are orthogonal, if any two chains intersect in at most one element, except the two longest chains that may only intersect in and 4-cube 4-cube Observe: orthogonal edge-disjoint
Edge-disjoint and orthogonal SCDs Question: How many pairwise edge-disjoint/orthogonal SCDs can we hope for? is an upper bound: even every SCD uses exactly one of those edges Conjecture [Shearer, Kleitman 79]: The -cube has pairwise orthogonal SCDs. Theorem [Shearer, Kleitman 79]: The standard construction and its complements are two orthogonal SCDs. Theorem [Spink 17]: The -cube has three pairwise orthogonal SCDs for .
Our results Theorem 1: The -cube has four pw. orthogonal SCDs for . Theorem 2: The -cube has five pw. edge-disjoint SCDs for . Proof of Theorem 2: Product lemma: If the -cube and -cube have SCDs each, then the -cube has edge-disjoint SCDs. find five edge-disjoint SCDs for dimensions Fact: If and are coprime, then every negative integer multiple of and . edge-disjoint and is a non- computer search in the necklace poset Proof of Theorem 1: similar, but more complicated product lemma due to [Spink 17] find four orthogonal SCDs for dimensions and
The central levels problem -cube Middle levels conjecture: The subgraph of the -cube induced by the middle two levels and has a Hamilton cycle. problem with a long history answered positively in [M. 16] Central levels conjecture: The subgraph of the -cube induced by the middle levels has a Hamilton cycle for any . raised by [Savage 93], [Gregor, krekovski 10], [Shen, Williams 15]
The central levels problem -cube known results: Central levels conjecture: The subgraph of the -cube induced by the middle [Gray 53] [El-Hashash, Hassan 01], [Locke, Stong 03] levels has a Hamilton cycle for any . [Gregor, krekovski 10] ??? [M. 16]
Our results Theorem 3: The -cube has a Hamilton cycle through the middle four levels ( ) for all . Theorem 4: The -cube has a cycle factor through the middle for all and . levels spanning collection of disjoint cycles
The central levels problem Proof: Theorem 4: The -cube has a cycle factor through the middle for all and . levels consider two edge-disjoint SCDs as the dimension is odd, all chains have odd length, even after restricting to middle levels taking every second edge yields two edge-disjoint perfect matchings their union is a cycle factor
Open problems Conjecture [Shearer, Kleitman 79]: The -cube has pairwise orthogonal SCDs. known: four we conjecture that the -cube has pairwise edge- disjoint SCDs. known: five central levels problem: Can the cycles in the factor be joined to a single Hamilton cycle? Structure of the cycle factor? efficient algorithms to generate those cycles first open case: middle six levels exploit new SCD constructions in other applications (Venn diagrams etc.)