Exploring Interior Angles in Polygons
Investigate and calculate the sum of interior angles in polygons, explore relationships between angle measures and number of sides, and apply formulas to determine missing angles. Utilize a protractor for accurate measurements and identify patterns within the results.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
LO: CALCULATING ANGLES IN POLYGONS W A L T : W A L T : I N V E S T I G A T E T H E S U M O F I N T E R I O R I N V E S T I G A T E T H E S U M O F I N T E R I O R A N G L E S I N P O L Y G O N S A N G L E S I N P O L Y G O N S O B S E R V E P A T T E R N S D U R I N G O B S E R V E P A T T E R N S D U R I N G I N V E S T I G A T I O N S I N V E S T I G A T I O N S M A K E P R E D I C T I O N S A N D D R A W M A K E P R E D I C T I O N S A N D D R A W C O N C L U S I O N S C O N C L U S I O N S
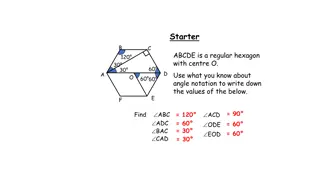
What do we know about these triangles? What do we know about these triangles?
If a = 44 degrees and b = 63 degrees what is If a = 44 degrees and b = 63 degrees what is angle c? angle c?
SUCCESS CRITERIA Measure the angles accurately using a Measure the angles accurately using a protractor protractor Round final answer to the nearest 10 Round final answer to the nearest 10 degrees degrees Look for patterns with the results Look for patterns with the results Investigate the relationship between the Investigate the relationship between the number of sides and interior angles number of sides and interior angles Find a rule Find a rule Check the rule works for irregular Check the rule works for irregular polygons polygons
WHAT FORMULA DO WE USE AND WHY? The interior angles of a triangle = 180 The interior angles of a triangle = 180 The interior angles of a quadrilateral = The interior angles of a quadrilateral = 360 360 That is because it can be split into 2 That is because it can be split into 2 triangles (180 +180= 360) triangles (180 +180= 360) The interior angles of a pentagon = 540 The interior angles of a pentagon = 540 That is because it can be split into 3 That is because it can be split into 3 triangles (180 +180 +180 = 540) triangles (180 +180 +180 = 540)
EACH TIME WE ADD ANOTHER SIDE WE ADD ANOTHER 180 DEGREES
SO THE RULE IS: Sum of Interior Angles = (n n-2) 180 Each Angle (of a Regular Polygon) = (n n-2) 180 / n n
SO DOES IT WORK FOR ALL IRREGULAR POLYGONS TOO?
SO DOES IT WORK FOR ALL IRREGULAR POLYGONS TOO? Yes because they can be split into Yes because they can be split into triangles too! triangles too!
PLENARY WHAT DOES THIS DIAGRAM TELL YOU ABOUT EXTERIOR AND INTERIOR ANGLES?