Understanding Polygons: Shapes with Many Angles

Explore the world of polygons, two-dimensional closed figures composed of straight line segments. Learn about their characteristics, types like equiangular and equilateral polygons, and examples of regular polygons.

• Polygons
• Shapes
• Angles
• Equiangular
• Equilateral

arrow Follow

Uploaded on Jul 16, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. Polygons The word polygon is a Greek word. Poly means many and gon means angles.

2. Polygons The word polygon means many angles A two dimensional object A closed figure Polygons

3. More about Polygons Made up of three or more straight line segments There are exactly two sides that meet at a vertex The sides do not cross each other Polygons

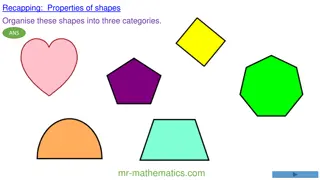
4. Examples of Polygons Polygons

5. These are not Polygons Polygons

6. Terminology Side: One of the line segments that make up a polygon. Vertex: Point where two sides meet. Polygons

7. Vertex Side Polygons

8. Interior angle: An angle formed by two adjacent sides inside the polygon. Exterior angle: An angle formed by two adjacent sides outside the polygon. Polygons

9. Exterior angle Interior angle Polygons

10. Let us recapitulate Exterior angle Vertex Side Diagonal Interior angle Polygons

11. Types of Polygons Equiangular Polygon: a polygon in which all of the angles are equal Equilateral Polygon: a polygon in which all of the sides are the same length Polygons

12. Regular Polygon: a polygon where all the angles are equal and all of the sides are the same length. They are both equilateral and equiangular Polygons

13. Examples of Regular Polygons Polygons

14. A convex polygon: A polygon whose each of the interior angle measures less than 180 . If one or more than one angle in a polygon measures more than 180 then it is known as concave polygon. (Think: concave has a "cave" in it) Polygons

15. IN TERIOR ANGLES OF A POLYGON Polygons

16. Let us find the connection between the number of sides, number of diagonals and the number of triangles of a polygon. Polygons

17. 180o 180o 180o 180o 180o 4 sides Quadrilateral 5 sides Pentagon 3 x 180 2 x 180o = 360o 2 o = 540 o 3 1 diagonal 2 diagonals 180o 180o 180o 180o 180o 180o 180o 180o 180o 6 sides Hexagon Heptagon/Septagon 7 sides 4 x 180o = 720o 4 5 x 180o = 900o 5 3 diagonals 4 diagonals Polygons

18. Regular Polygon No. of sides No. of diagonals No. of Sum of the interior angles Each interior angle 0 0/3 0 Triangle 3 0 1 180 180 = 60 Polygons

19. Regular Polygon No. of sides No. of diagonals No. of Sum of the interior angles Each interior angle 0 0/3 0 Triangle 3 0 1 180 180 = 60 0 0/4 0 Quadrilateral 4 1 2 2 x180 = 360 360 = 90 0 Polygons

20. Regular Polygon No. of sides No. of diagonals No. of Sum of the interior angles Each interior angle 0 0/3 0 Triangle 3 0 1 180 180 = 60 0 0/4 0 Quadrilateral 4 1 2 2 x180 = 360 360 = 90 0 0 0/5 Pentagon 5 2 3 3 x180 = 540 540 = 108 0 0 Polygons

21. Regular Polygon No. of sides No. of diagonals No. of Sum of the interior angles Each interior angle 0 0/3 0 Triangle 3 0 1 180 180 = 60 0 0/4 0 Quadrilateral 4 1 2 2 x180 = 360 360 = 90 0 0 0/5 Pentagon 5 2 3 3 x180 = 540 540 = 108 0 0 0 0/6 Hexagon 6 3 4 4 x180 = 720 720 = 120 0 0 Polygons

22. Regular Polygon No. of sides No. of diagonals No. of Sum of the interior angles Each interior angle 0 0/3 0 Triangle 3 0 1 180 180 = 60 0 0/4 0 Quadrilateral 4 1 2 2 x180 = 360 360 = 90 0 0 0/5 Pentagon 5 2 3 3 x180 = 540 540 = 108 0 0 0 0/6 Hexagon 6 3 4 4 x180 = 720 720 = 120 0 0 0 0/7 Heptagon 7 4 5 5 x180 = 900 900 = 128.3 0 0 Polygons

23. Regular Polygon No. of sides No. of diagonals No. of Sum of the interior angles Each interior angle 0 0/3 0 Triangle 3 0 1 180 180 = 60 360 = 90 0 0/4 0 Quadrilateral 4 1 2 2 x180 = 360 0 0 0/5 Pentagon 5 2 3 3 x180 = 540 540 = 108 0 0 0 0/6 Hexagon 6 3 4 4 x180 = 720 720 = 120 0 0 0 0/7 Heptagon 7 4 5 5 x180 = 900 900 = 128.3 0 0 n sided polygon n Association with no. of sides Association with no. of sides Association with no. of triangles Association with sum of interior angles Polygons

24. Regular Polygon No. of sides No. of diagonals No. of Sum of the interior angles Each interior angle 0 0/3 0 Triangle 3 0 1 180 180 = 60 0 0/4 0 Quadrilateral 4 1 2 2 x180 = 360 360 = 90 0 0 0/5 Pentagon 5 2 3 3 x180 = 540 540 = 108 0 0 0 0/6 Hexagon 6 3 4 4 x180 = 720 720 = 120 0 0 0 0/7 Heptagon 7 4 5 5 x180 = 900 900 = 128.3 0 0 n sided polygon n n - 3 n - 2 (n - 2) x180 (n - 2) x180 0 0 / n Polygons

25. 1 Calculate the Sum of Interior Angles and each interior angle of each of these regular polygons. 7 sides Septagon/Heptagon Sum of Int. Angles 900o Interior Angle 128.6o 2 3 4 9 sides 10 sides 11 sides Nonagon Sum 1260o I.A. 140o Decagon Sum 1440o I.A. 144o Hendecagon Sum 1620o I.A. 147.3o Polygons

26. Diagrams not drawn accurately. Find the unknown angles below. x 100o 75o 95o w 115o 75o 70o 110o 2 x 180o = 360o 360 245 = 115o 3 x 180o = 540o 540 395 = 145o 125o 125o z 100o 140o 138o 105o 121o 138o 117o y 133o 137o 4 x 180o = 720o 720 603 = 117o 5 x 180o = 900o 900 776 = 124o Polygons

27. EXTERIOR ANGLES OF A POLYGON Polygons

28. An exterior angle of a regular polygon is formed by extending one side of the polygon. Angle CDY is an exterior angle to angle CDE B A C F 1 2 E D Y 0 Exterior Angle + Interior Angle of a regular polygon =180 Polygons

29. 1200 600 1200 600 600 1200 Polygons

30. 1200 1200 1200 Polygons

31. 1200 1200 1200 Polygons

32. 3600 Polygons

33. 600 600 600 600 600 600 Polygons

34. 600 600 600 600 600 600 Polygons

35. 3 4 600 600 2 600 600 5 600 600 1 6 Polygons

36. 3 4 600 600 2 600 600 5 600 600 1 6 Polygons

37. 3 4 2 3600 5 1 6 Polygons

38. 900 900 900 900 Polygons

39. 900 900 900 900 Polygons

40. 900 900 900 900 Polygons

41. 2 3 3600 1 4 Polygons

42. No matter what type of polygon we have, the sum of the exterior angles is ALWAYS equal to 360 . Sum of exterior angles = 360 Polygons

43. In a regular polygon with n sides 0 Sum of interior angles = (n -2) x 180 i.e. 2(n 2) x right angles Exterior Angle + Interior Angle =180 0 0/n Each exterior angle = 360 0/exterior angle No. of sides = 360 Polygons

44. Let us explore few more problems Find the measure of each interior angle of a polygon with 9 sides. Ans : 140 Find the measure of each exterior angle of a regular decagon. Ans : 36 How many sides are there in a regular polygon if each interior angle measures 165 Ans : 24 sides Is it possible to have a regular polygon with an exterior angle equal to 40 Ans : Yes 0 0 0? 0 ? Polygons

45. Thank You Polygons DG

46. This powerpoint was kindly donated to www.worldofteaching.com Home to well over a thousand free powerpoint presentations submitted by teachers. This a free site. Please visit and I hope it will help in your teaching