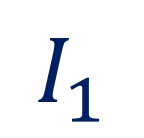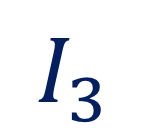Dispersing Points on Intervals

Given non-overlapping intervals on a line, find a point on each interval to maximize the minimum distance between pairwise points. Explore a greedy algorithm approach and insights on spacing points evenly for optimized results.

• Dispersing Points
• Intervals
• Minimum Distances
• Greedy Algorithm
• Optimization

harlei Follow

Uploaded on Feb 24, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Dispersing Points on Intervals Shimin Li and Haitao Wang Utah State University

2. Problem Definition Given ? non-overlapping intervals on a line . Find a point on each interval. Objective: Maximize the minimum distance of any pairwise points ?1 ?2 ?3 ?4 ?1 ?2 ?3 ?4

3. The Cycle Version ?1 ?2 ?2 ?1 In a cycle version, the intervals are arcs on a cycle ?. ?3 ?3 ?4 ?4

4. Previous Work and Our Results Previous Work: Two or high-dimensional space Many problem variations, NP-hard in general 1D No previous work particularly on 1D Our Result (for 1D): An ?(?) time greedy algorithm

5. An Example ?1 ?2 ?3 ?4 ?1 ?2 ?3 ?4 |?1?2| |?2?3| The minimum distance is ?1?2 = |?2?3|

6. Notation ?? ?? ?? ?? ?? ?? ?? ?? ??: The ?-th interval ??: The left endpoint of ?? ??: The right endpoint of ?? ??: The point on ??

7. An Observation Spacing points evenly can maximize the minimum distance ?? ?? ?? ?? ?? ???? ?? ?? ? ?

8. An Observation(Cont.) ?? ?? ? ? ????= min 1 ?<? ? An O(n2) time algorithm: ?? ?? ? ?, for 1 ? < ? ?. Compute each value of ???= Improve to ?(?) time.

9. A Greedy Algorithm Place points on intervals from left to right. Place the first point on the left endpoint of ?1. ?1 ?1 ????: The current minimum distance ????= +

10. A Greedy Algorithm (Cont.) Try to maximize the minimum distance. ?1 ?2 ?1 ?2 Its position may be changed later ????= |?1?2|

11. A Greedy Algorithm (Cont.) Try to decrease the minimum distance as small as possible. Pending Points Their positions may be changed later ?1 ?3 ?2 ?3 ?1 ?2 ????=|?1?3| ????= |?1?2| 3 1

12. An Example(Case I) ?3 ?1 ?2 ?3 ?2 ?1 ????= |?1?2| ?2+ ???? ?3 ????= |?1?2|

13. An Example(Case II) ?3 ?1 ?2 ?3 ?2 ?1 ????= |?1?2| ?3< ?2+ ???? ?3 ????= ?1?2 = ?2?3

14. An Example(Case III) ?3 ?1 ?2 ?3 ?2 ?1 ????=|?1?3| ????= |?1?2| ?3< ?2+ ???? 2 ?3 ?1 ?2 ?3 ?2 ?1 ????=|?2?3| ????= |?1?2| ?3< ?2+ ???? 2

15. Case III in General ??+2 ??+1 ??+4 ?? ??+3 ??+2 ??+4 ??+1 ?? Checking every interval takes ?(?) time in total, resulting an overall ?(?2) time An ?(?) time algorithm: The key idea: Maintain a critical list of intervals. We only need to check the intervals in the list from left to right. Once an interval is checked, we can remove it from the list. Overall time: ?(?) ??+3

16. Another Observation ?? could be removed from the critical list. ?? ? ?? ?? ?? ? ??+1 ?? ? ?? ?? ?? ?? ?? ? ??+1

17. Another Observation (Cont.) ?? should be checked earlier than following intervals in the critical list. ? ?? ?? ? ?? ?? ? ??+1 ?? ?? ?? ?? ?? ? ??+1 ??

18. An Example ?19 ?8 ?16 ?6 ?19 ?16 ?6 ?8 ?8 ?6 8 6>?16 ?6 ?16 ?8 16 8>?19 ?8 16 6 19 8

19. A Critical List of Intervals ?? ?? ?? +1 ?? +1 ?? ?? ?? ?? (? = ?1) ?? +1 ?? ? +1 ? >?? ?? ? ? (? ? < ? +1 ?)

20. A Summary Maintain a critical list of intervals Update the list in ?(1) amortized time for processing each interval Total time: ?(?)

21. The Cycle Version ?1 ?2 ?2 ?1 In a cycle version, the intervals are arcs on a cycle ?. ?3 ?3 ?4 ?4

22. Convert it to a Line Version ?1 ?2 ?4 ?1 ?4 ?4 ?3 ?1 Where should we cut the cycle ? to a line segment? ?2 ?2 ?3 ?3 ?1 ?3 ?2 ?4 ?3 ?1 ?2 ?4

23. Duplicate the Line Segment ?1 ?2 ?4 ?4 ? 3 ? 1 ?1 ?3 ?2 ?4 ? 2 Let ????=|?| ?, initially. ?3 ?1 ?2 ?2 ?4 ? 1 ? 1 ? 2 ? 3 ? 3 ? 4 ?3 ? 2 ?3 ?4 ?1 ? 4

24. Thanks!