Bloom Filters and Count-Min Sketches Explained
Bloom Filters and Count-Min Sketches are essential data structures in computer science for efficient data querying and approximation algorithms. Bloom Filters help determine if an element is likely present in a set, while Count-Min Sketches estimate frequencies of elements in streams of data. These image-rich explanations provide insights into their functionalities, implementations, and use cases.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
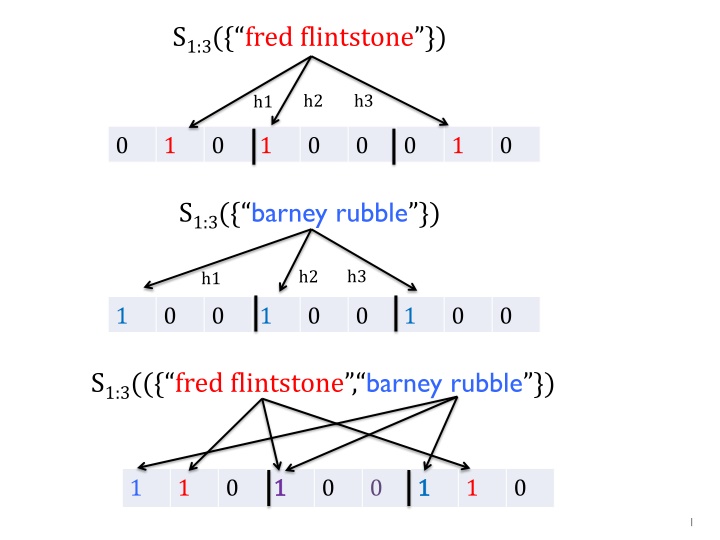
S1:3({fred flintstone}) h2 h3 h1 0 1 0 1 0 0 0 1 0 S1:3({ barney rubble }) h3 h2 h1 1 0 0 1 0 0 1 0 0 S1:3(({ fred flintstone , barney rubble }) 1 1 0 1 1 0 0 1 1 1 0 1
Bloom filters a variant split the bit vector into k ranges, one for each hash function 0 0 0 0 0 0 0 0 0 bf.contains( fred flintstore ): return AND of all hashed bits h3 h1 h2 1 1 0 1 1 0 0 1 1 1 0 bf.contains( pebbles ): h3 h2 h1 1 1 0 1 1 0 0 1 1 1 0 2
Bloom filters a variant split the bit vector into k ranges, one for each hash function 0 0 0 0 0 0 0 0 0 a false positive! bf.contains( pebbles ): h3 h2 h1 1 1 0 1 1 0 0 1 1 1 0 3
BLOOM FILTERS COUNT -MIN SKETCHES 4
Count-min sketches split a real vector into k ranges, one for each hash function 0 0 0 0 0 0 0 0 0 cm.inc( fred flintstone , 3): add the value to each hash location h3 h1 h2 0 3 0 3 0 0 0 3 0 cm.inc( barney rubble ,5): h3 h2 h1 5 3 0 8 8 0 0 5 5 3 0 5
Count-min sketches split a real vector into k ranges, one for each hash function 0 0 0 0 0 0 0 0 0 3 cm.get( fred flintstone ): take minwhen retrieving a value h3 h1 h2 5 3 0 8 8 0 0 5 5 3 0 5 cm.get( barney rubble): h3 h2 h1 5 3 0 8 8 0 0 5 5 3 0 6
Count-min sketches split a real vector into k ranges, one for each hash function value retrieved for s is ??? cm.add(s,??) has been called cm.get( barney rubble): h3 h2 h1 5 3 0 8 8 0 0 5 5 if T is sum of all ?? values for any s, then Prob(error > T?) < ? 3 0 cm.add( pebbles , 2): h3 h2 h1 7 3 0 10 10 0 0 5 5 5 0 7
Count-min sketches Equivalently, use a matrix, and each hash leads to a different row ? = 2/? cm.inc( fred flintstone , 3): d = log1/? 0 3 0 3 0 3 0 0 0 cm.inc( barney rubble ,5): 5 8 5 3 0 3 0 0 0 8