Binary Trees and Their Applications

Binary trees are data structures consisting of nodes, each with children and a parent. They find use in Huffman coding, decision trees, and sentence parsing, facilitating efficient data storage and retrieval.

• Binary Trees
• Data Structures
• Huffman Coding
• Decision Trees
• Applications

zamarron_a Follow

Uploaded on Feb 23, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Binary Tree (Intro)

2. ADT Tree: Review Trees: made of nodes One type of data (like lists) Each Node in a tree has: 0 or more children (successors) Each node can have many children! 1 parent (predecessor) Except tree s root: 0 predecessors Root is start of a tree

3. Subset of Trees Each Node in a BINARY tree has: Binary Tree: Review 0, 1, or 2 children(successors) 1 parent (predecessor) Except tree s root: 0 predecessors Root is start of a tree

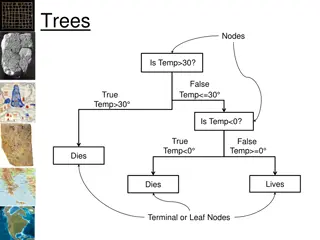
4. Examples of Binary Trees: Huffman Code: Sentence parsing Seriously cool method for coming up with a compressed data encoding scheme Basic idea: (Alphabet is easiest example): Before Huffman code: each character is represented with 8 bits. But e occurs much more frequently than z Wouldn t it make sense to make the e have a 3 or 4 bit representation, even if the z had to have, say, a 13 character representation? Huffman code systematically takes any data set and figures out a representational code, such that the data that occurs most frequently has the shortest bit representation, and those that occur the least frequently have the most bits for representation Decision trees You ve probably seen these: Cool part: None of the short bit representations are prefixes to the longer bit representations!!!! E.g., running shoes: Running Shoes E.g., If e is represented as 101 Do you run more than 15 miles per week? NO OTHER letter s bit representation starts with 101! Maybe z would be 1101011101001 Yes No The first 3 bits of ALL other characters are NOT 101 Do you have flat feet? Does style matter to you? So you can store 1011101011101001101 And know that that is eze! Yes No Yes No

5. class NodeT { int data; NodeT *left; //left child NodeT *right; // right child NodeT *parent; //NULL for root of tree //optional: int height; // height up from lowest descendent leaf public: NodeT(int x); ~NodeT(); void printNodeT(); }; Node Class Definition for a Binary Tree:

6. Subsets of Tree ADT Each node only has 0, 1, or 2 children Trees can have 0 or more children Each node has a left child, a right child, and a parent Binary Tree TakeAways: Each node may also have a height (max height of its 2 children + 1) Leaves (no children) have a height of 1 Examples of binary trees: Huffman code (just so cool!) Decision trees: a boatload of online quizzes are decision trees Sentence parsing