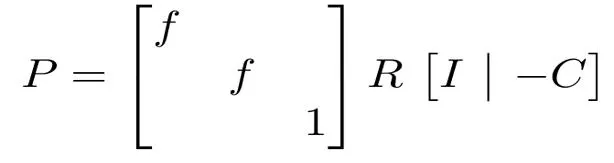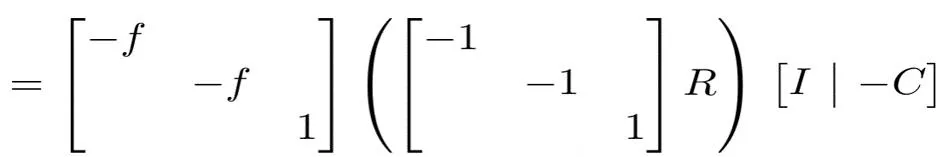A Formulation for Unknown Focal Length
A detailed exploration of solving for unknown focal length in camera pose estimation problems, addressing redundancies, introducing a new parameterization method, and discussing novel applications. The formulation allows for more efficient and accurate solutions in scenarios with varying complexities.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
A Formulation for Unknown Focal Length Changchang wu Google
Directly Solving for Focal Length? There is a two fold redundancy Negated focal length additional rotation around z by 180 Leads to 2X solutions, and slower minimal solver The problem exists in both absolute pose and relative pose
Getting Around such Redundancies? Sometimes there is a pattern of f^2 Relative pose with unknown focal length Modeling the problems differently Absolute pose with unknown focal length (P4P) 3D Point distance (ratio) -> over-determined Null space -> not general Sometimes you are unlucky Absolute pose with one also unknown radial distortion 12 meaningful solutions out of 24 in Josephson et al. CVPR 2009
A New Parameterization Separate the rotation around the Z axis Combine the rotation around the Z axis with focal length The same number of parameters (Dof) without the redundancy Possible degeneracy with f = 0 (any ) is reduced to (fc = fs = 0)
Application : P4P -> P3.5P (Wu CVPR 2015) Truly minimal (using exactly 7 coordinates) Allows to work with single coordinates Exactly the minimal 10 solution Extra coordinate can be used for solution filtering Simpler polynomial system & faster GB solver
Other Applications Relative pose between generalized camera and uncalibrated pinhole See our Structure-less resection poster at 3A-1 Reduces the number of solutions by half (e.g. 100->50 for 5+2) Absolute pose with unknown focal length & radial distortion Reduces the number of solutions from 24 to 12 Using a different radial distortion model. Feels like symmetry?