Realistic Particle Representations and Interactions in Emission & Regeneration UFT
The presentation explores a model in which particles are depicted as focal points in space, proposed by Osvaldo Domann. It delves into theoretical particle representations, motivation for a new approach, and the methodology behind the Postulated model. Additionally, it delves into particle representations in the Emission & Regeneration UFT, discussing subatomic particles as focal points of rays of Fundamental Particles and their distribution of relativistic energy. The interaction laws between various particles are also examined, highlighting interactions between static particles, moving particles, and their corresponding longitudinal and transversal fields.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
1 Emission & Regeneration UFT A model where particles are represented as focal points in space. Osvaldo Domann
2 Theoretical representations of particles. Existent particle models Proposed particle model Focal point in space Vortex Point-like Wave-packet Strings etc.
3 Motivation for a new approach and the methodology Postulated
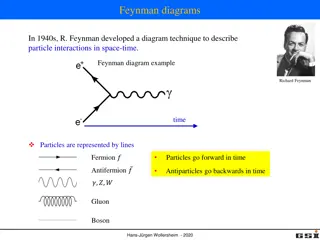
4 Particle representation in the Emission & Regeneration UFT Subatomic Particles represented as Focal Points of rays of Fundamental Particles (FPs) transversa l Fundamental Particles longitudin al p p
5 Particles as focal points Distribution in space of the relativistic energy of a BSP with v c Fundamental particle + = + 2 o 2 p = E E E E E where e s n 2 p + E 2 o + Focal point E = = E E s n 2 o 2 p 2 o 2 p E E E E 1 r d d d = sin o dr 2 2 2 r = = dE E d J e e e = = dE E d J s s s = = dE E d J p n n n d dV=r2 dr sin d FP 2 n Opposed angular momenta
6 Linear momentum out of opposed angular momenta = h dE h = = = = dE dE E d Nh Nh 1 c dE NdE J n n h = h dE c n = n h h h Subatomic particle n J h h c = dp dE = c dp h h h Focus 1 c N c = = p dE n h h = h dE h h h c c h h = 7 dE = h 2.088 10 eV h h h h h= 5 10 s 7 -1 Photon
7 Particles as focal points Definition of field magnitudes dH based on Energy and angular momenta of FPs = = dH s dE d s d s J Longitudinal emitted field e e e e e e = = dH s s dE d s d s J Longitudinal regenerating field s s = = dH n n dE d n d n J Transversal regenerating field n n Characteristics of the introduced fundamental particles (FPs) Fundamental Particles are postulated. FPs move with light or infinite speed relative to the focal point. FPs store energy as rotations in moving and transversal directions FPs interact through their angular momenta or dH fields. Pairs of FPs with opposed transversal angular momenta generate linear momenta on subatomic particles.
Interactions between particles 8 Interaction laws between two SPs (electrons and positrons) 1) Interaction between two static SPs (Coulomb) 2) Interaction between two moving SPs (Ampere, Lorentz, Bragg, Gravitation) 3) Interaction between a moving and a static SP ( Induction, Maxwell, Gravitation) To these three interactions between SPs correspond the three following interactions between their longitudinal and transversal dH fields. s s = dE dH dH 1) Longitudinal X longitudinal (Coulomb) 1 2 p s s 1 2 n n = dE dH dH 2) Transversal X transversal (Ampere) 1 2 p n n 1 2 = dE dH dH 3) Transversal * longitudinal (Induction) p n s p The three following slides show each interaction in detail.
Interactions between particles 9 1) Interaction law between two static SPs (Coulomb) dH s = J d s dE = dH s dH s 1 2 p e s 1 2 r r e s 1 = dp dE p c ( ) l d s s 1 e s = 1 2 dp s H d H d s stat R e r s r R 2 c R 1 1 2 2 R r r 1 2
10 Interactions between particles 2) Interaction law between two moving SPs (Ampere, Lorentz , Bragg and gravitation) ( ) n = dE dH n dH n with 1 1 2 n n 1 2 = dH n J d n in i in in i i 1 c = ( ) 1 n dp E 1 ( ) l d n n = 1 2 dp s H d H d s dyn R n r n r R 2 c R 1 1 2 2 R r r 1 2
Interactions between particles 11 3) Interaction law between a moving and a static SP (Maxwell, Gravitation) Induction law 1 l d 2 n ( ) n = dp s H d H d s ind R n rr s r R c R p p R rr r p
12 Motivation and Methodology Postulated
Coulomb at atomic distances 13 Linear momentum as a function of the distance between static BSPs stat p Coulomb Nuclei core o o+- Migrated electron or positron ooo Swarm of electrons and positrons +- o Electrons and positrons that migrate outsite the nucleus core are reintegrated or expulsed. Reintegration generates the gravitation forces while expulsion radioactivity.
14 Zone of migrated electrons and positrons Momentum wall Zone of nucleus core Tunneling of and particles d 1 p d d 2 V(d) = t 0
15 Potential energy o o+- ooo Nuclei core Swarm of electrons and positrons
Newton and Ampere gravitation forces 16 Gravitation between two neutrons due to parallel and aligned reintegration of migrated BSPs Neutrons composed of electrons and positrons Nuclei core Nuclei core Newton component Ampere component Gravitation is explained with the electromagnetic induction and Ampere laws. No difference between inertial and passive-gravitational mass exists.
Newton and Ampere gravitation forces 17 Total gravitation force due to the reintegration of BSPs Ampere component Newton component G R = F F F = M M T G R 1 2 2 d d R F For galactic distances the Newton component can be neglected and explains: with a positive sign the flattening of galaxie s speed curve without the need of dark matter with a negative sign the expansion of galaxies without the need of dark energy. The gravitation is compatible with QM.
18 Differences between the SM and the E&R Model Four carriers X: Photons W, Z Bosons Gluons Gravitons Four fields: Electromagnetic Weak Strong Gravitation Particle representation: Point-like Interactions: Each carrier defines a different interaction No carriers: Only one field: dH field Particle representation: Focal point of rays of FPs with longitudinal and Transversal angular momenta Interactions: Cross- and scalar-products of the longitudinal and transversal angular momenta of FPs define the interactions. 18
19 Relativity is a speed problem and not a space-time problem + + + = + + + 2 x 2 y 2 z 2 c 2 x 2 y 2 z 2 c v v v v v v v v Optical lenses Electric antennas Interfaces Galilei relativity multiplied with the relativistic factor Result: 1/2 = 2 2 (1 / ) v c Space and time are absolute variables
20 Stern-Gerlach experiment Magnetic spin due to the interaction between the orbit electron and the charge of the nucleus Conclusion: Magnetic spin is not an intrinsic characteristic of the electron
21 Quarks Quarks with fraction charges 2 u=3 1 3 d = Electric charge of the proton (uud) 2 2 1 3 3 3 + = 1 Interpretation E&R model 9 91 positrons 918 electrons N N N + + uN +uN +dN =1 (u, d are relative charges) Swarm of electrons and positrons N = 1837 u u P = 1837 A B C + N N + N N = u i i i i i N i A B C d + 2N =332 positrons 3 2N =76 positrons 3 N N = d + i i N N i i i N A i N = 498 A B No fractional electric charge 1N =407 electrons 3 C Conclusion: No violation of charge conservation No strong forces are required to hold quarks together
22 Epicycles to match calculated with experimental data No epicycles required Planet O Sun 500 years because of particular interests of established scientists Heliocentric model
23 Conclusions of E&R UFT : o Electrons and positrons neither attract nor repel each other for the distance between them 0 o o o o o Atomic nucleus o o o o o o oo o Epicycles introduced during the last 150 years Swarm of electrons and positrons Examples Epicycles of the SM Special relativity General relativity Stern-Gerlach Coexistence of protons in nuclei Radioactivity Flattening of galaxie s curve Expansion of galaxie s Quarks Time dilation and length contraction Curvature of space (Gravitons) Electron intrinsic magnetic spin Strong force (Gluons) Weak force (W, Z Bosons) Dark matter Dark energy Fraction of electric charge Q/e Conclusion: Statements that epicycles are experimentally confirmed are fallacies. The only statement that can be made is that the model is consistent.
24 Thank you for your attention, The complete work is available at www.odomann.com Osvaldo Domann odomann@yahoo.com