A Circle Property
A Circle Property
Risp 9
A
B
Now on axes, plot the points A and B.
Using compasses, draw the circle that has AB as diameter.
What is the equation of your circle?
Do you notice anything unusual about your circle?
Compare your circle with those your colleagues have drawn.
What do they all have in common?
Resources
SIC_5
SIC_5
Properties of circles by solving a mathematical problem involving picking numbers and creating points on a circle. Discover how every circle through the origin and derive the equation of the circle using midpoint and radius concepts. By completing the square, see the circle centered at the midpoint of the diameter. Dive into the unique characteristics of circles and compare your findings with colleagues for a deeper understanding.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
A Circle Property Risp 9
A Circle Property I'm going to pick a number, let's say... 12. Pick four numbers, any numbers, let's call them p, q, s, and t, where: p and q multiply to 12, and s and t multiply to -12. Now create the points (p, s) and (q, t). Record your values in a table to avoid confusion.
p q product s t product 12 -12 ( p , s ) ( q , t ) A B Now on axes, plot the points A and B. Using compasses, draw the circle that has AB as diameter. What is the equation of your circle? Do you notice anything unusual about your circle? Compare your circle with those your colleagues have drawn. What do they all have in common?
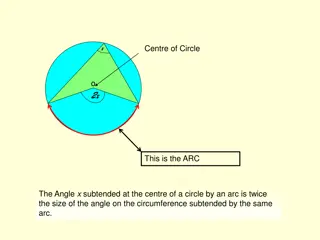
Why does every such circle go through the origin? ?+? 2,?+? Midpoint of the diameter is: 2 1 2 1 2 Radius is: ? ?2+ ? ?2 2 2 ?+? 2 ?+? 2 =1 Equation of circle: ? ?2+ ? ?2 ? + ? 4 ?2 ? + ? ? +1 4? + ?2+ ?2 ? + ? ? +1 4? + ?2=1 ? ?2+ ? ?2 4 ?2+ ?2 ? + ? ? ? + ? ? +1 4?2+ 2?? + ?2+ ?2+ 2?? + ?2= 1 4?2 2?? + ?2+ ?2 2?? + ?2 ?2+ ?2 ? + ? ? ? + ? ? +1 44?? + 4?? = 0 ?2+ ?2 ? + ? ? ? + ? ? + ?? + ?? = 0 But ?? = ?? so ?? + ?? = 0
So ?2+ ?2 ? + ? ? ? + ? ? = 0 This is always satisfied if ? and ? are both zero. Hence (0,0) always lies on the circle. Complete the square on the above equation to satisfy yourself that it is the equation of a circle centred on the midpoint of AB with a radius equal to the distance from the origin to that midpoint. 2 2 ? 1 1 4? + ?2+ ? 1 1 4? + ?2= 0 2? + ? 2? + ? 2 2 ? 1 + ? 1 =1 4? + ?2+1 4? + ?2 2? + ? 2? + ?
So ?2+ ?2 ? + ? ? ? + ? ? = 0 This is always satisfied if ? and ? are both zero. Hence (0,0) always lies on the circle. Complete the square on the above equation to satisfy yourself that it is the equation of a circle centred on the midpoint of AB with a radius equal to the distance from the origin to that midpoint. 2 2 ? 1 1 4? + ?2+ ? 1 1 4? + ?2= 0 2? + ? 2? + ? 2 2 ? 1 + ? 1 =1 4? + ?2+1 4? + ?2 2? + ? 2? + ?
SIC_5 SIC_5
