Understanding the Rule of Mixtures in Composite Materials
The Rule of Mixtures (ROM) is a weighted method for predicting the properties of composite materials, such as fiber-reinforced polymers (FRP). This method relies on assumptions regarding the homogeneity and properties of fibers and matrices. By combining volume fraction and properties linearly, the
5 views • 23 slides
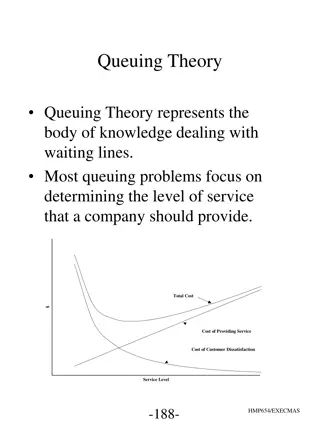
Understanding Queuing Theory and its Characteristics
Queuing Theory is the study of waiting lines and service levels in businesses. It involves analyzing customer arrival patterns, service configurations, and queuing processes such as FIFO vs. LIFO disciplines. Characteristics include the generation of customers, homogeneity of populations, and determ
1 views • 25 slides
Exploring Binomial and Poisson Distributions in Probability Theory
Understand the fundamentals of binomial and Poisson distributions through practical examples involving oil reserve exploration and dice rolling. Learn how to calculate the mean, variance, and expected outcomes of random variables in these distributions using formulas and probability concepts.
0 views • 13 slides
Understanding Basic Concepts in Statistics
This content covers fundamental concepts in statistics such as populations, samples, models, and probability distributions. It explains the differences between populations and samples, the importance of models in describing populations, and discusses various distributions like the normal and Poisson
0 views • 42 slides
Understanding Binomial and Poisson Data Analysis
Discrete data, including Binomial and Poisson data, plays a crucial role in statistical analysis. This content explores the nature of discrete data, the concepts of Binomial and Poisson data, assumptions for Binomial distribution, mean, standard deviation, examples, and considerations for charting a
2 views • 31 slides
Understanding Probabilistic Models: Examples and Solutions
This content delves into probabilistic models, focusing on computing probabilities by conditioning, independent random variables, and Poisson distributions. Examples and solutions are provided to enhance understanding and application. It covers scenarios such as accidents in an insurance company, ge
0 views • 12 slides
Understanding Renewal Processes in Continuous Time
Renewal theory is a branch of probability theory that extends Poisson processes for various inter-arrival times. A renewal process models randomly occurring events over time, such as customer arrivals at a service station or natural phenomena like earthquakes. This article delves into the concept of
0 views • 20 slides
Understanding Overdispersed Data in SAS for Regression Analysis
Explore the concept of overdispersion in count and binary data, its causes, consequences, and how to account for it in regression analysis using SAS. Learn about Poisson and binomial distributions, along with common techniques like Poisson regression and logistic regression. Gain insights into handl
0 views • 61 slides
Understanding Invariance in Posterior Distributions
Exploring the insensitivity of posterior distributions to variations in prior distributions using a Poisson model applied to pancreas data. The analysis involves calculating posterior mean and standard deviation with different Gamma prior distributions. Results showcase minimal change in outcomes ac
0 views • 7 slides
Understanding Discrete Probability Distributions
Explore the definition of random variables, probability distributions, and three types of discrete distributions - Binomial, Hypergeometric, and Poisson. Learn about the mean, variance, and standard deviation of probability distributions, as well as the difference between discrete and continuous dis
3 views • 32 slides
Covariant Phase Space Formalism in Nonabelian Gauge Theories
The presentation focuses on the covariant phase space formalism in nonabelian gauge theories, aiming to derive the symplectic form and Poisson/Dirac brackets systematically from the Lagrangian. By applying canonical quantization methods, the structure of the infrared sector in such theories can be d
0 views • 42 slides
Analysis of Mosquito Collection Data: Net Weight, Water Coating, and Model Fitting
This analysis includes tables detailing the weight of batch 13 nets, mean water and insecticide for coating the net, model fitting of Poisson models for mosquito count dataset, and modeling fitting of ZIP and ZINB models for trap collection data. The tables provide valuable insights into net propert
0 views • 5 slides
Understanding Geometric and Poisson Probability Distributions
Explore the geometric and Poisson probability distributions, including criteria for geometric random variables, formulas, and practical examples. Learn how to calculate probabilities using the geometric distribution and apply it in scenarios like Russian Roulette and blood donor collection. Dive int
0 views • 13 slides
Birth and Death Processes in Population Dynamics
Birth and death processes in population dynamics involve the concept of how organisms reproduce and die, leading to changes in population size over time. These processes can be generalized from the Poisson process and are crucial in queuing theory and modeling dynamic systems. The differential-diffe
0 views • 20 slides
Understanding Continuous-Time Markov Chains in Manufacturing Systems
Explore the world of Continuous-Time Markov Chains (CTMC) in manufacturing systems through the lens of stochastic processes and performance analysis. Learn about basic definitions, characteristics, and behaviors of CTMC, including homogeneous CTMC and Poisson arrivals. Gain insights into the memoryl
0 views • 50 slides
Understanding Statistical Distributions in Physics
Exploring the connections between binomial, Poisson, and Gaussian distributions, this material delves into probabilities, change of variables, and cumulative distribution functions within the context of experimental methods in nuclear, particle, and astro physics. Gain insights into key concepts, su
0 views • 13 slides
Statistical Learning: Discrete Random Variables and Distributions
Explore the concepts related to discrete random variables and their corresponding probability density functions, such as Poisson Distribution and Binomial Distribution. Understand the implications of negative values in random variables, calculate expected values, and grasp the relationships between
0 views • 16 slides
Exploring Variability and Noise in Neural Networks
Understanding the variability of spike trains and sources of variability in neural networks, dissecting if variability is equivalent to noise. Delving into the Poisson model, stochastic spike arrival, and firing, and biological modeling of neural networks. Examining variability in different brain re
0 views • 71 slides
Computational Earth Science: Solving Heat Flow in Objects with Complex Shapes Using Finite Difference Method
Explore projects involving the Finite Difference Method for solving static heat conduction problems, also known as the Poisson Equation. Topics include testing boundary conditions, symmetry of solutions, point sources, dipoles, and more. Gain insights into changing boundary conditions and understand
0 views • 20 slides
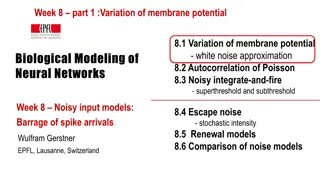
Exploring Noisy Output in Neural Networks: From Escape Rate to Soft Threshold
Delve into the intricacies of noisy output in neural networks through topics such as the variation of membrane potential with white noise approximation, autocorrelation of Poisson processes, and the effects of noise on integrate-and-fire systems, both superthreshold and subthreshold. This exploratio
0 views • 34 slides
Exploring Membrane Potential Variations in Neural Networks
Delve into the dynamics of membrane potential variations in neural networks through topics like white noise approximation, autocorrelation of Poisson processes, and the Noisy Integrate-and-Fire model. Investigate how these variations manifest at different thresholds, shedding light on the biological
0 views • 63 slides
Understanding Probability Distributions in Engineering Mathematics-III
Explore the concept of random variables, types of distributions such as binomial, hypergeometric, and Poisson, and the distinction between discrete and continuous variables. Enhance your knowledge of probability distributions with practical examples and application scenarios.
0 views • 57 slides
Distribution Functions & Examples in Statistics
Explore distribution functions in statistics including binomial, Poisson, exponential, and normal distributions. Examples demonstrate calculations for probabilities, means, variances, and using distribution approximations. Understand concepts through practical scenarios like airplane hits, coin flip
0 views • 15 slides
Understanding Binomial Distribution: Examples and Visualizations
Explore various problems and examples related to the binomial distribution, including calculating probabilities, approximations using Poisson distribution, and visual representations. Discover how binomial distribution tends towards normal under different conditions and learn how to solve problems u
0 views • 9 slides