Understanding Queuing Theory and its Characteristics

Queuing Theory is the study of waiting lines and service levels in businesses. It involves analyzing customer arrival patterns, service configurations, and queuing processes such as FIFO vs. LIFO disciplines. Characteristics include the generation of customers, homogeneity of populations, and deterministic vs. stochastic arrivals. The concepts of Poisson probability distribution and service rates are also explored, shedding light on the dynamics of queuing systems and the importance of efficient service management.

• Queuing Theory
• Waiting lines
• Service levels
• Customer arrival patterns
• Stochastic arrivals

ema Follow

Uploaded on Jul 16, 2024 | 1 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

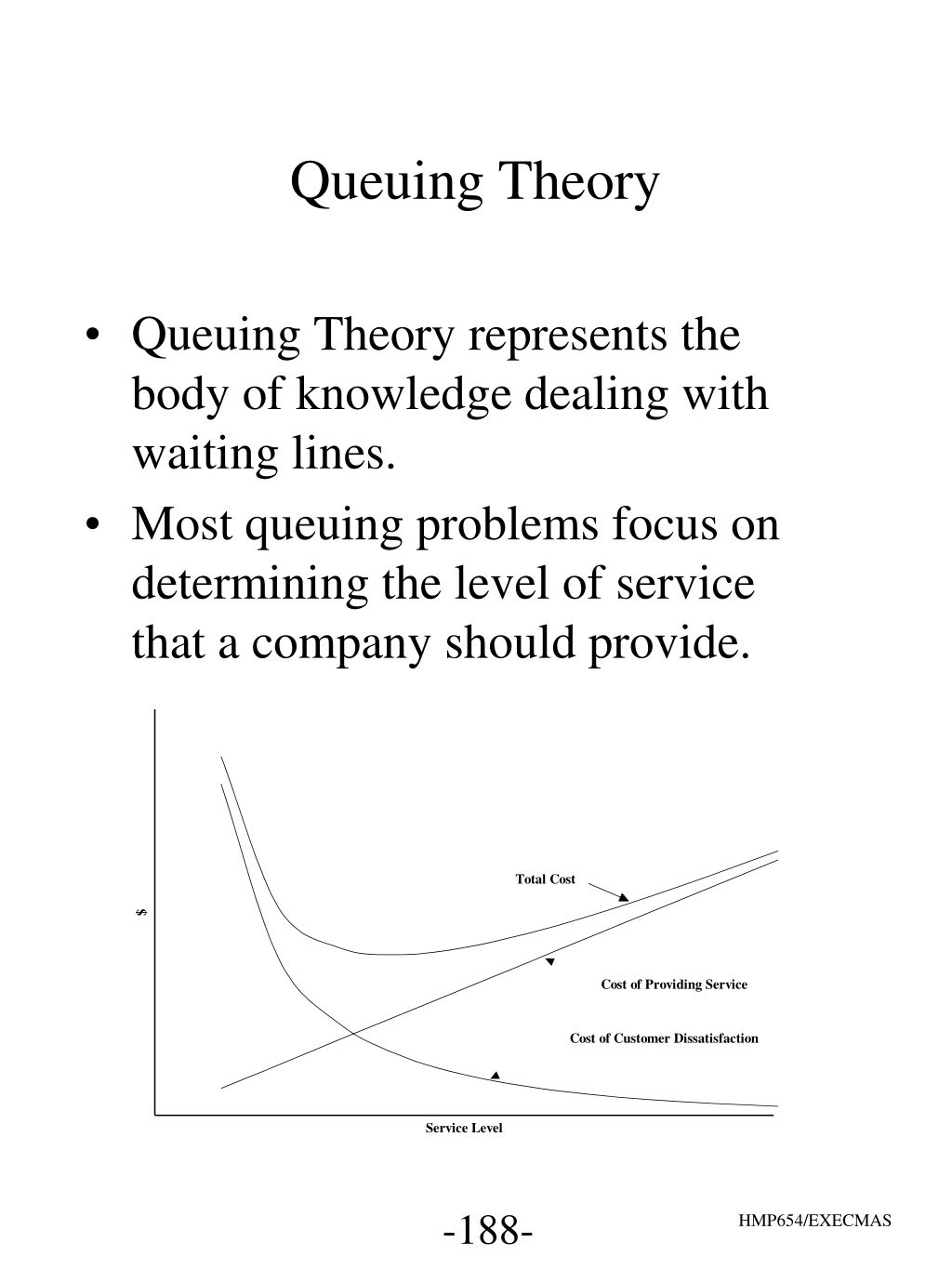
1. Queuing Theory Queuing Theory represents the body of knowledge dealing with waiting lines. Most queuing problems focus on determining the level of service that a company should provide. Total Cost $ Cost of Providing Service Cost of Customer Dissatisfaction Service Level -188- HMP654/EXECMAS

2. Queuing Theory Queuing Systems Configurations Customer Arrives Customer Leaves Server Waiting Line Customer Leaves Server 1 Customer Arrives Customer Leaves Server 2 Waiting Line Customer Leaves Server 3 Customer Arrives Customer Leaves Server 1 Waiting Line Customer Arrives Customer Leaves Server 2 Waiting Line Customer Arrives Customer Leaves Waiting Line Server 3 -189- HMP654/EXECMAS

3. Queuing Theory Characteristics of a Queuing Process Generation of Customers Infinite vs. Finite calling population Homogeneity of the calling population Individual vs. Batch arrivals Deterministic vs. Stochastic arrivals Queuing of Customers Single vs. Multiple servers Finite vs. Infinite queues -190- HMP654/EXECMAS

4. Queuing Theory Characteristics of a Queuing Process FIFO vs. LIFO disciplines Priority rules Servicing the Customers Deterministic vs. Stochastic service time Individual vs. Batch Processing -191- HMP654/EXECMAS

5. Queuing Theory Characteristics of a Queuing Process Generation of Customers Poisson probability distribution x e x = p x ( ) ! x represents the number of arrivals in a specific time period. represents the arrival rate , that is, the average number of arrivals per time period. -192- HMP654/EXECMAS

6. Queuing Theory Arrival Rate The time between arrivals is known as the interarrival time. If the number of arrivals in a given period follows a Poisson distribution, with mean , the interarrival times follow an exponential probability distribution with mean 1/ The exponential distribution exhibit the memoryless property. An arrival process is memoryless if the time until the next arrival occurs does not depend on how much time has elapsed since the last arrival. -193- HMP654/EXECMAS

7. Queuing Theory Arrival Rate -194- HMP654/EXECMAS

8. Queuing Theory Service Rate Queue time is the amount of time a customer spends waiting in line for service to begin. Service time is the amount of time a customer spends at a service facility once the actual performance of service begins. Service time is often model as an exponential random variable ( ) T, = 1 p t T e for T 0 -195- HMP654/EXECMAS

9. Queuing Theory Service Rate The service rate, denoted by , represents the average number of customers that can be served per time period. The average service time per customer is 1/ time periods. -196- HMP654/EXECMAS

10. Queuing Theory Kendall Notation 1/2/3 1 The first characteristic identifies the nature of the arrival process using the following standard abbreviations: M = Markovian interarrival times (following an exponential distribution) D = Deterministic interarrival times (not random) -197- HMP654/EXECMAS

11. Queuing Theory Kendall Notation 2 The second characteristic identifies the nature of the service times using the following standard abbreviations: M = Markovian service times G = General service times (following a non-exponential distribution) D = Deterministic service times (not random) 3 The third characteristic indicates the number of servers available. -198- HMP654/EXECMAS

12. Queuing Theory Operating Characteristics U - Utilization factor, or the percentage of time that all servers are busy. P0 - Probability that there are no units in the system. Lq- Average number of units in line waiting for service L - Average number of units in the system (in line and being served) Wq - Average time a unit spends in line waiting for service T - Actual time a unit spends in the queue W - Average time a unit spends in the system (in line and being served) Pw - Probability that an arriving unit has to wait for service Pn- Probability of n units in the system -199- HMP654/EXECMAS

13. Queuing Theory The M/M/s Model There are s servers in the system, where s is a positive integer Arrivals follow a Poisson distribution and occur at an average rate of per time period Each server provides service at an average rate of per time period, and actual service times follow an exponential distribution Arrivals wait in a single FIFO queue and are serviced by the first available server < s -200- HMP654/EXECMAS

14. Queuing Theory Formulas describing the M/M/s Model = U s 1 n s 1 s s = + P 0 ! ! n s s = 0 n + 1 s P 0 = L q 2 ( ) 1 ! s s = + L L q L q = W q -201- HMP654/EXECMAS

15. Queuing Theory Formulas describing the M/M/s Model 1 = + W W q s 1 s = P P 0 w ! s s n = , P P for n s 0 n ! n n = P P for n 0 , s ( ) n n s s s ! s ! ( ) ( ) = = 1 s t , p T t Pe 0 ( ) 1 s s -202- HMP654/EXECMAS

16. Queuing Theory Q.xls -203- HMP654/EXECMAS

17. Queuing Theory Case Problem (A) p. 140 Prime Health is a large fictitious preferred provider organization (PPO) operating in the Southwest. Like all PPOs, Prime Health realizes the importance of carefully managing the extent to which its primary care providers refer patients to specialists. Prime Health s contract with their primary care physicians therefore requires care provider must obtain authorization for the referral from the PPO. The primary care physician typically obtains the required authorization by having an office assistant telephone the PPO office, where a single authorization clerk is available to handle the request. If the authorization clerk is busy with another call, then the subsequent callers are placed on hold, and their calls are handled by the authorization clerk in the order in which they arrived. Because of the importance of receiving the required authorization, the office assistant never hangs up before talking with the authorization clerk. However, a survey conducted by the PPO among its provider network reveals that extreme dissatisfaction results if the wait exceeds five minutes. Prime Health has determined from a special study conducted during the past month that calls arrive at an average rate of 18 per hour. The same study reveals that the PPO operator requires an average of two minutes to process a given call. Thus the average service rate is 30 per hour. Operation of such a system involves a number of costs: 1. The authorization clerk employed by the PPO earns a salary of $9.80 per hour including benefits. 2. The office assistant who places the telephone request for the authorization earns a salary of $8.35 per hour including benefits. 3. While the office assistant is on hold, he or she is unable to perform any additional productive functions for the office. 4. The cost associated with adding an additional telephone line to the PPO system is $50.00 per month, including prorated installation costs. For such a system, a number of questions could be raised. The physicians offices are quite interested in answering the following questions: 1. How often will the office assistant be placed on hold? 2. How long will the office assistant need to wait until the call is handled? 3. Will the office assistant ever receive a busy signal? The PPO is also concerned with a number of issues. These might include: 1. The amount of time that the authorization clerk is idle; 2. The improvement in service that results from adding a second clerk; 3. The number of incoming lines needed to provide a particular level of service; 4. The fraction of incoming calls when the time on hold exceeds the maximum tolerable level of five minutes. -204- HMP654/EXECMAS

18. Queuing Theory Case Problem (cont.) M/M/s queuing computations Arrival rate Service rate Number of servers Utilization P(0), probability that the system is empty Lq, expected queue length L, expected number in system Wq, expected time in queue W, expected total time in system Probability that a customer waits 18 30 Assumes Poisson process for arrivals and services. 1 (max of 40) 60.00% 0.4000 0.9000 1.5000 0.0500 0.0833 0.6000 0.4 PROBABILITY 0.2 0 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 NUMBER IN SYSTEM -205- HMP654/EXECMAS

19. Queuing Theory Case Problem (cont.) Probability that the Time in Queue is Greater than t for Selected Values of t (Basic Single-Server System) t (minutes) p( T > t ) P0 = s = = = = 0 1 2 3 4 5 6 7 8 9 0.6 0.4 0.491238 0.402192 0.329287 0.269597 0.220728 0.180717 0.147958 0.121138 0.099179 0.081201 1 30 18 0.6 10 -206- HMP654/EXECMAS

20. Queuing Theory Case Problem (cont.) M/M/s queuing computations Arrival rate Service rate Number of servers Utilization P(0), probability that the system is empty Lq, expected queue length L, expected number in system Wq, expected time in queue W, expected total time in system Probability that a customer waits 18 30 Assumes Poisson process for arrivals and services. 2 (max of 40) 30.00% 0.5385 0.0593 0.6593 0.0033 0.0366 0.1385 0.6 0.4 PROBABILITY 0.2 0 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 NUMBER IN SYSTEM -207- HMP654/EXECMAS

21. Queuing Theory Case Problem (cont.) Probability that the Time in Queue is Greater than t for Selected Values of t (Basic Two-Server System) t (minutes) p( T > t ) P0 = s = = = = 0 1 2 3 4 5 6 7 8 9 0.138471 0.068763 0.034147 0.016957 0.00842 0.004181 0.002076 0.001031 0.000512 0.000254 0.000126 0.5385 2 30 18 0.3 10 -208- HMP654/EXECMAS

22. Queuing Theory Finite Queue Model Case Problem (cont.) M/M/s with Finite Queue Arrival rate Service rate Number of servers Maximum queue length Utilization P(0), probability that the system is empty Lq, expected queue length L, expected number in system Wq, expected time in queue W, expected total time in system Probability that a customer waits Probability that a customer balks 18 30 1 5 (max of 40) (max of 40 combined) 58.85% 0.4115 0.7099 1.2984 0.0394 0.0728 0.5885 0.0192 0.6 0.4 PROBABILITY 0.2 0 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 NUMBER IN SYSTEM -209- HMP654/EXECMAS

23. Queuing Theory Finite Queue Model Case Problem (cont.) M/M/s with Finite Queue Arrival rate Service rate Number of servers Maximum queue length Utilization P(0), probability that the system is empty Lq, expected queue length L, expected number in system Wq, expected time in queue W, expected total time in system Probability that a customer waits Probability that a customer balks 18 30 2 5 (max of 40) (max of 40 combined) 29.99% 0.5385 0.0587 0.6586 0.0033 0.0366 0.1384 0.0002 0.6 0.4 PROBABILITY 0.2 0 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 NUMBER IN SYSTEM -210- HMP654/EXECMAS

24. Queuing Theory Case Problem (cont.) Exp. Time in Queue (minutes) No. of Clerks No. of Hold Positions Utilization Factor p(Busy) 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 0 1 2 3 4 5 6 7 8 9 0.375 0.184 0.099 0.056 0.033 0.019 0.011 0.007 0.004 0.002 0 0.1011 0.0294 0.0088 0.0026 0.0008 0.0002 0.0001 0 0.0198 0.0039 0.0008 0.0002 0 0 0.375 0.490 0.540 0.566 0.580 0.588 0.593 0.596 0.598 0.599 0.600 0.270 0.291 0.297 0.299 0.300 0.300 0.300 0.300 0.196 0.199 0.200 0.200 0.200 0.75 1.35 1.81 2.16 2.41 2.6 2.73 2.82 2.88 3 0 0.101 0.157 0.182 0.192 0.196 0.197 0.198 0 0.013 0.018 0.02 0.021 infinite 0 1 2 3 4 5 6 infinite 0 1 2 3 infinite -211- HMP654/EXECMAS

25. Queuing Theory Case Problem (cont.) Monthly Cost of Lines Monthly Cost of Clerks Monthly Cost of Waiting Total Monthly Cost Exp. No. in System Configuration 1 Clerk, 5 hold positions 2 Clerk, 2 hold positions 3 Clerk, 0 hold positions $300 200 150 $1,699 3,397 5,096 1.2984 0.6414 0.5881 $1,879 $3,878 4,525 6,097 928 851 Authorization clerk's monthly salary = $9.80/h x 40 h/week x 4.333 weeks/month = $1,698.66 Office assistant's monthly salary = $8.35/h x 40 h/week x 4.333 weeks/month = $1,447.33 -212- HMP654/EXECMAS