Numerical Methods for Approximating Analytic Equations
Introduction to approximating solutions to analytic equations, focusing on differential equations, integral equations, and integro-differential equations. Exploring ordinary and partial derivatives, differential and integral equations, and the involvement of unknown functions and their derivatives a
4 views • 15 slides
Introduction to Partial Budgeting in Farm Management
Understand the purpose and methodology of partial budgets in farm management, focusing on analyzing net gains from small changes or refinements to farm operations. Learn how to build and utilize partial budgets to make informed decisions regarding farm management. Explore examples of farm management
2 views • 20 slides
The Pathophysiology of Epilepsy and Seizures
Epilepsy is a group of disorders characterized by recurrent, unprovoked seizures. Seizures are sudden surges of electrical activity in the brain that can cause alterations in sensation, behavior, or consciousness. They can be classified as partial or generalized based on their origin and clinical ma
2 views • 14 slides
Maxwell Equations in Thermodynamics
In thermodynamics, Maxwell equations are derived using Euler's reciprocity relation. They involve characteristic functions such as internal energy, free energy, enthalpy, and Gibbs free energy, along with parameters like temperature, entropy, pressure, and volume. These equations form the foundation
1 views • 15 slides
Differential Equations of First Order & Higher Degree: Lecture 18
This lecture covers differential equations of first order but not of the first degree, general forms of such equations, methods for solving them, and examples of differential equations to be solved. The content includes detailed explanations, equations, solutions, and problem-solving techniques.
0 views • 9 slides
WBC Differential Count in Blood Analysis
WBC (white blood cell) count is essential in assessing a patient's health. A differential count helps determine the percentage of different types of white blood cells. This analysis can provide important insights into various health conditions like infections, allergies, and systemic illnesses. The
2 views • 9 slides
Linear Equations in Algebra: A Comprehensive Overview
An exploration of algebraic expressions, equations, and linear equations in one variable with detailed explanations and examples. Discover the fundamental concepts, solving methods, and applications of linear equations in various word problems. Master the art of transforming mathematical expressions
0 views • 15 slides
Differential Leveling in Surveying
Differential leveling is a crucial aspect of surveying that involves determining the elevation of points with respect to a reference datum. This process includes various key elements such as benchmark, back sight, fore sight, and change points. By utilizing methods like the Height of Instrument and
2 views • 12 slides
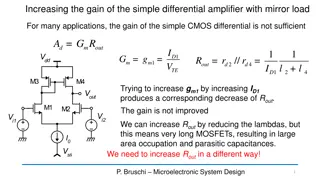
Techniques to Increase Gain in a Simple Differential Amplifier
Explore methods to boost the gain of a simple CMOS differential amplifier by replacing the current mirror with a cascode mirror, adding a common-gate stage, and employing a cascode differential amplifier. These techniques help improve Rout without extensive use of long MOSFETs, optimizing the amplif
3 views • 30 slides
Differential Equations: Types, Classification, and Solutions
Differential equations are mathematical equations that relate independent and dependent variables through differential coefficients. They can be classified as ordinary or partial, based on the types of derivatives involved. The order and degree of a differential equation, as well as its linearity an
4 views • 26 slides
Differential Equations in Economics Honours
Differential equations, introduced by Newton and Leibniz in the 17th century, play a key role in economics. These equations involve derivatives and represent implicit functional relationships between variables and their differentials, often related to time functions. The order and degree of a differ
1 views • 16 slides
Introduction to Differential Equations and Laplace Equations
Understanding differential equations of various orders, solving methods, linear and non-linear equations, ordinary and partial differential equations, definitions of solutions, and general vs. particular solutions in the context of Differential Equations and Laplace Equations.
4 views • 20 slides
Numerical Methods and Errors in Computation
Delve into the world of numerical methods through the guidance of Dr. M. Mohamed Surputheen. Explore topics such as solving algebraic and transcendental equations, simultaneous linear algebraic equations, interpolation, numerical integration, and solving ordinary differential equations. Learn about
0 views • 130 slides
Partial Fraction Decomposition
The partial fraction decomposition method is a powerful technique used to simplify rational functions by breaking them into simpler fractions. It involves reducing the degree of either the numerator or the denominator. Learn about proper and improper fractions, simple and repeated factors, and how t
0 views • 17 slides
Differential Equations: Basics to Applications
Differential equations are fundamental in mathematics, with various types such as first-order, partial, and Clairaut's equations explored in this content. The content covers general equations, solutions, and examples, providing insights into linear and higher-order equations with constant coefficien
0 views • 20 slides
Partial Differential Equations of Second Order
Exploring the concepts of second-order partial differential equations in mathematics, including the general form, linear equations with variable coefficients, and equations with constant coefficients. Learn about integral solutions, examples, and techniques for solving these equations with detailed
0 views • 21 slides
Three-Dimensional Systems of Linear Ordinary Differential Equations
Explore the concepts of three-dimensional linear systems of ordinary differential equations, including techniques for finding eigenvalues and the general solutions. Learn how to determine characteristic polynomials for 3x3 matrices and identify sink, source, and saddle points in 3D systems.
0 views • 20 slides
Ordinary Differential Equations (ODEs) in Mathematics
Ordinary Differential Equations (ODEs) play a crucial role in modeling various physical phenomena and engineering problems. This lecture delves into the basics of ODEs, discussing their applications, solution methods, and interpretation in real-world scenarios. Mathematical modeling is highlighted a
1 views • 19 slides
Introduction to Numerical Methods: A Comprehensive Overview
Numerical methods play a crucial role in solving mathematical problems efficiently through arithmetic operations. This lecture by Dr. Nur Uddin covers the fundamental concepts of numerical methods, emphasizing their importance in engineering problem-solving with the use of modern digital computers.
1 views • 17 slides
Solving Exponential Equations Algebraically
Learn how to solve exponential equations algebraically with the same base and unlike bases. Understand the properties of equality for exponential equations and practice solving various equations step by step. Improve your skills in rewriting equations with the same base and applying the rules of exp
0 views • 9 slides
Differential Equations in Physical Phenomena
Differential equations play a crucial role in modeling physical phenomena involving rates of change like fluid motion, mechanical systems, and heat dissipation. This content explores examples of differential equations in motion and provides insights on sketching direction fields using tools like Map
0 views • 11 slides
Geometric Algebra and Calculus: A Deep Dive into Vector Derivatives and Maxwell Equations
Explore the world of geometric algebra and calculus through topics such as vector derivatives, Cauchy-Riemann equations, Maxwell equations, and spacetime physics. Unify diverse mathematical concepts to gain insights into analytic functions, differential operators, and directed integration.
0 views • 20 slides
GCSE Algebra Revision Materials and Equations Practice
Explore a collection of GCSE algebra revision materials, including solving linear equations and common mishaps in algebraic simplification. Practice setting up equations and solving linear equations with provided examples and questions. Enhance your algebra skills through comprehensive content desig
0 views • 15 slides
CMRR in Differential Amplifiers
Differential input amplifiers, including operational, instrumentation, and difference amplifiers, play a crucial role in amplifying differential signals while rejecting common-mode noise. The Common-Mode Rejection Ratio (CMRR) is a key parameter in these amplifiers, indicating their ability to suppr
0 views • 48 slides
Zero or Partial Percepts in Search
In the context of search with zero or partial percepts, agents may not have complete information about the current state in a partially observable environment. This article outlines the challenges of searching in such scenarios, including situations where agents have no observations or only partial
0 views • 20 slides
Applications of Differential Equations in Engineering and Mathematics
Exploring the practical applications of differential equations, specifically focusing on Newton's Law of Cooling and Orthogonal Trajectories. The concept of exact differential equations and their solutions, along with real-life examples demonstrating temperature changes over time, are discussed. Und
0 views • 11 slides
Second-Order RLC Circuits in Electronics
Explore second-order RLC circuits in electronics, characterized by second-order differential equations and involving resistors, inductors, capacitors, and voltage sources. Learn about initial and final values of voltage and current, applications in filters, and the differential equations governing t
0 views • 13 slides
Classical Mechanics and Mathematical Methods Lecture 20 Overview
The lecture covered solutions of differential equations using Green's function methods based on eigenfunction expansions. Topics included finding formal solutions, motivations behind Green's functions, and understanding Sturm-Liouville equations for homogenous and inhomogenous problems. Students had
0 views • 29 slides
Stochastic Differential Equations and Numerical Integration
Explore the concepts of Brownian motion, integration of stochastic differential equations, and derivations by Einstein and Langevin. Learn about the assumptions, forces, and numerical integration methods in the context of stochastic processes. Discover the key results and equations that characterize
0 views • 6 slides
Differential Privacy in Statistical Analysis
Gain insight into the concept of differential privacy in statistical analysis through key terminologies, foundational ideas, and practical examples. Explore the balance between data privacy and statistical quality, and learn how differential privacy serves as a mathematical guarantee to protect indi
1 views • 28 slides
Dynamic Function for Basal Area of Trees Derived from Differential Equation
Mathematical methods presented by Braun and Simmons are used to derive a dynamic function for the basal area of individual trees from a production-theoretically motivated autonomous differential equation. The differential equation and general dynamic function are described, highlighting the relation
0 views • 45 slides
Partial Differential Equations (PDEs) in Numerical Methods
Explore the world of Partial Differential Equations (PDEs) in the context of numerical methods. Learn about PDE classification, linear and nonlinear PDEs, notation, representing solutions, and applications like the heat equation. Dive into examples and concepts to enhance your understanding.
0 views • 69 slides
Solving Differential Equations: Methods and Techniques
Learn how to solve differential equations using methods like separation of variables and sketch families of solution curves. Understand the process of finding general and particular solutions to equations, and explore a variety of exercises and examples to enhance your understanding. Master the art
0 views • 16 slides
The Challenges of Protecting Privacy with Differential Privacy
The article discusses the motivation behind using differential privacy to protect sensitive data while enabling useful queries. It highlights the promise of differential privacy, challenges faced, attacks on existing systems like PINQ and Airavat, and introduces a defense system called The Fuzz. The
0 views • 24 slides
Partial Molar Quantities and Chemical Potential
Exploring partial molar quantities and chemical potential in thermodynamics helps us understand how system variables change with composition alterations. Through concepts like partial molar volumes and Gibbs free energy, we can delve into the intricate dynamics of thermodynamic systems and their beh
0 views • 23 slides
Comprehensive Overview of Mathematical Methods and Resources
Covering topics such as interpolation, curve fitting, algebraic equations, transcendental equations, numerical differentiation, integration, Fourier series, Fourier transforms, partial differential equations, vector calculus, and finite difference methods. Includes recommended textbooks and referenc
0 views • 150 slides
Overview of Finite Difference Methods in Computational Fluid Dynamics
Discretization of equations is crucial in CFD, and Finite Difference Methods play a key role. Utilizing Taylor series, forward differences, rearward differences, and central differences, these methods transform partial differential equations into solvable algebraic forms. Understanding these techniq
0 views • 32 slides
Differential Equations and Boundary Value Problems
Explore the world of Differential Equations (DE) with a focus on Boundary Value Problems, guided by Dennis G. Zill and Michael R. Cullen. Dive into the realm of First Order and Higher Order DE, Partial DE, Laplace Transform, Fourier Series, and more. Unravel the complexities of DE through various se
0 views • 33 slides
Fixpoint Equations in Programming Languages
Fixpoint equations play a crucial role in programming languages for solving mutually recursive problems like parsing and dataflow analysis. This content explores the concepts of fixpoint equations, assumptions for ensuring solutions, computing solutions, and generalizations for cases with greatest e
0 views • 31 slides
Masking and Partial Loudness in Sound Perception
Masking in sound perception involves the phenomenon where changes in total loudness do not occur despite adding or removing signals, due to partial loudness variations across frequencies. This concept is crucial for comprehending how we perceive sound and the limitations of our auditory system, part
0 views • 31 slides