AQA Level 2 Certificate in Further Maths
The AQA Level 2 Certificate in Further Maths is designed for high-achieving students to develop advanced skills in algebra, geometry, calculus, matrices, trigonometry, functions, and graphs. The course covers topics like number fractions, decimals, algebraic fractions, coordinate geometry, calculus,
7 views • 9 slides
Exporting STATA Results to Excel Using PutExcel Feature
Learn how to utilize the PutExcel feature in STATA to effortlessly export your results to an Excel file. With PutExcel, you can export matrices, stored results, images, estimation tables, and even add formulas for calculations. This tool streamlines the process of transferring statistical data to Ex
6 views • 32 slides
Matrix Systems in Restorative Dentistry: A Comprehensive Overview
Understanding the role of matrices and retainers in restorative dentistry is crucial for achieving optimal results in direct restorative procedures. This article covers the definitions, ideal requirements, functions, and parts of matrices, providing valuable insights into their importance and usage
1 views • 55 slides
2x2 Matrices in Political Science: An Irreverent Perspective
Delve into the world of 2x2 matrices in political science with a humorous twist, uncovering their foibles, fallacies, and effectiveness. From youthful rigidity to complex behavioral continuums, this unconventional take on matrices unveils their application in various scenarios like spouse choices, b
2 views • 34 slides
Matrices: Types, Definitions, and Operations
Matrices are ordered arrays used to express linear equations. Learn about types, definition, equality, and operations like addition, subtraction, and multiplication. Discover matrix equality and the transpose of a matrix, including symmetric and skew-symmetric matrices.
2 views • 17 slides
Linear Transformations and Matrices in Mathematics
Linear transformations play a crucial role in the study of vector spaces and matrices. They involve mapping vectors from one space to another while maintaining certain properties. This summary covers the introduction to linear transformations, the kernel and range of a transformation, matrices for l
1 views • 85 slides
Matrices in Precalculus: Order, Augmented Matrix, and Row-Echelon Form
Delve into the world of matrices in Precalculus with a focus on identifying matrix orders, creating augmented matrices for systems of equations, transforming matrices into row-echelon form, and solving linear equations using matrices. Explore elementary row operations, row-echelon form, and reduced
2 views • 37 slides
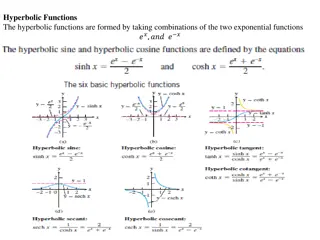
Hyperbolic Functions and Their Inverses
This content delves into the world of hyperbolic functions, discussing their formation from exponential functions, identities, derivatives, and inverse hyperbolic functions. The text explores crucial concepts such as hyperbolic trigonometric identities, derivatives of hyperbolic functions, and integ
1 views • 9 slides
Inverse Probability Weights in Epidemiological Analyses
In epidemiological analyses, inverse probability weights play a crucial role in addressing issues such as sampling, confounding, missingness, and censoring. By reshaping the data through up-weighting or down-weighting observations based on probabilities, biases can be mitigated effectively. Differen
1 views • 25 slides
Singular Value Decomposition
The Singular Value Decomposition (SVD) is a powerful factorization method for matrices, extending the concept of eigenvectors and eigenvalues to non-symmetric matrices. This decomposition allows any matrix to be expressed as the product of three matrices: two orthogonal matrices and a diagonal matri
0 views • 35 slides
Immobilization of Enzymes in Biochemistry
Enzyme immobilization involves confining enzyme molecules to a distinct phase from substrates and products, attaching them to solid matrices for enhanced specificity and reduced inhibition. Inert polymers or inorganic materials are used as carrier matrices with methods like physical adsorption onto
0 views • 24 slides
Introduction to Matrices in Mathematical Analysis
Matrices play a crucial role in simplifying complex systems of equations and are well-suited for systematic mathematical treatments and computer computations. This introduction covers the definition of matrices, their properties such as size and notation, and various types of matrices including colu
0 views • 77 slides
Linear Algebra Review for Big Data Summer Institute
Join Rupam Bhattacharyya at the Big Data Summer Institute for a comprehensive review of linear algebra concepts. Explore topics such as matrix notation, special matrices, shapes of matrices, and matrix operations. Gain valuable insights for applications in big data analysis and machine learning.
0 views • 18 slides
States Analogous to 12C Hoyle State in Heavy Nuclei Using Inverse Kinematics
The study discusses the search for states similar to the 12C Hoyle state in heavier nuclei through the thick target inverse kinematics technique. It explores alpha clustering in nuclei, the thick target inverse kinematics method, events with alpha multiplicities, and more experimental details relate
0 views • 19 slides
Matrices and Solving Equations in Electrical Engineering
Matrices play a crucial role in solving linear equations in Electrical Engineering applications. Learn about matrix structures, special matrices, inverses, transposes, system of linear equations, and solving methods using MATLAB/Python. Explore the application of matrices in solving voltage-current
2 views • 24 slides
Inverse Condemnation Law in North Carolina
Explore the nuances of inverse condemnation law, including its history, basis in fundamental constitutional rights, N.C. statutory framework, attorney fees, and major categories of inverse takings. Learn about the actions, burdens of proof, and legal principles involved in these cases.
0 views • 36 slides
The Inverse Relationship of Addition and Subtraction
Learn about the inverse relationship between addition and subtraction through examples and visual aids. Practice writing inverse number sentences and understand how addition and subtraction are opposite operations that involve rearranging the same numbers in a different order.
3 views • 11 slides
Affinity Chromatography: A Breakthrough in Biochemical Research
Affinity chromatography, developed in the 1930s by A. Wilhelm Tiselius, is a vital technique for studying enzymes and proteins. It relies on the specific affinity between biochemical compounds and utilizes matrices like agarose for binding sites. Ligands such as amino and hydroxyl groups play crucia
1 views • 27 slides
Rank in Matrices
Rank in matrices represents the maximum number of independent columns, with implications for pivot columns, basic variables, and free variables. The rank of a matrix is essential for determining its properties and dependencies. Learn about rank-deficient matrices, basic versus free variables, and mo
0 views • 7 slides
Learning-Based Low-Rank Approximations and Linear Sketches
Exploring learning-based low-rank approximations and linear sketches in matrices, including techniques like dimensionality reduction, regression, and streaming algorithms. Discusses the use of random matrices, sparse matrices, and the concept of low-rank approximation through singular value decompos
0 views • 13 slides
Alpha Cluster Structure in Nuclei Using Thick Target Inverse Kinematics Technique
Exploring the alpha cluster structure of nuclei through the thick target inverse kinematics technique for multiple alpha decays. This study investigates alpha clustering in nuclei, potential alpha condensates, and the application of the inverse kinematics technique in detecting multiple alpha emissi
0 views • 14 slides
Flexible Framework for Stormwater Lids Modeling
A new flexible framework for forward and inverse modeling of stormwater lids is presented. It includes governing equations, hydraulic and contaminant transport, numerical methods, and demonstration cases for various green infrastructure components. The importance of different processes in modeling i
0 views • 20 slides
High-Resolution 3D Seafloor Topography Enhancement Using Kalman Filtering
Proposing a Kalman Filter approach to refine seafloor topography estimation by integrating various geophysical data types. The method allows for producing regional bathymetry with higher resolution, truncating unnecessary observations, and reducing the matrix dimensions in the inverse problem. Inclu
0 views • 9 slides
MATLAB Basics for Electrical Engineering Students
In this instructional content from the Government Polytechnic West Champaran Department of Electrical Engineering, students are introduced to the fundamentals of MATLAB. Topics covered include transposing matrices, concatenating matrices, matrix generators, arrays, entering matrices, and manipulatin
0 views • 48 slides
Advancements in Adding ECD to Matlab/Mathematica SUS Models
Enhancements in incorporating Eddy Current Damping (ECD) into Matlab and Mathematica SUS models for HAUX/HTTS testing have been made to streamline the integration process. This includes addressing challenges with damping implementation, exporting symbolic matrices, and utilizing state-space formalis
0 views • 11 slides
Generating Random Variables Using Inverse Transform Method
Explore the Inverse Transform Method for generating random variables in simulations. Learn how to map random instances to desired distributions, whether continuous or discrete, by understanding cumulative distribution functions and inverting them. Examples and step-by-step explanations provided for
0 views • 24 slides
Composite and Inverse Functions
Learn about composite functions, inverse functions, and how to find their compositions and inverses through examples and step-by-step explanations. Explore the concept of forming composite functions, verifying inverse functions, and finding the inverse of a function using interchange and solving met
0 views • 15 slides
Hazard Matrices and Impact-Based Forecasting
Hazard matrices are essential tools for coordinating emergency preparedness and response by categorizing primary, secondary, and tertiary effects of hazards. Impact matrices help organizations assess risks and determine potential impacts of events, allowing for better planning and mitigation strateg
0 views • 12 slides
Direct and Inverse Proportion in Mathematics
Exploring the concept of direct and inverse proportion in mathematics through various questions from past exam papers. The content includes images illustrating how these proportional relationships work in different scenarios.
0 views • 24 slides
Electron Beam Analysis and Optimization for RF Linac in Inverse Compton Scattering
This research activity report discusses the analysis and optimization of a 6D phase space electron beam for RF Linac-based Inverse Compton Scattering radiation sources. It covers the SPARC_LAB Thomson Source and ELI-NP GBS, including experiments, simulations, and studies on beam parameters and struc
0 views • 26 slides
Negative Numbers and Additive Inverse
Explore the world of negative numbers and additive inverse through a series of mathematical exercises. Learn how to calculate sums involving negatives and discover the concept of additive inverses, where adding a number and its opposite results in zero. Test your understanding with various numerical
0 views • 21 slides
Solving Systems of Equations using Inverse Matrices
Learn how to solve systems of equations using inverse matrices, find the determinant of matrices, use matrix multiplication, calculate the inverse matrix, and apply it to solve simultaneous equations. Explore examples and applications in investment scenarios.
0 views • 14 slides
Insights into Binning and Response Matrices for Spectral Analysis
Understanding the impact of binning and response matrices in spectral analysis, including energy bin properties, flux evaluation techniques, assumptions, and strategies for improvement. The discussion delves into challenges and solutions for accurate data interpretation and modeling in high-resoluti
0 views • 20 slides
Parallel Computation for Matrix Multiplication
Matrix multiplication is a fundamental operation with diverse applications across scientific research. Parallel computation for matrix multiplication involves distributing the computational workload over multiple processors, improving efficiency. Different algorithms have been developed for multiply
0 views • 36 slides
Robotic Kinematics & Control: Exploring Parallel Robots & Delta Robots
Discover the fascinating world of robotic kinematics and control through the exploration of parallel robots, Stewart platforms, inverse kinematics, forward kinematics, multiple solutions, and Delta robots. From understanding the structure of control variables to solving kinematic equations, this con
0 views • 15 slides
Solving Trigonometric Equations with Inverse Functions
Learn how to solve trigonometric equations using inverse trigonometric functions with step-by-step examples. Understand the concept of sin⁻¹, cos⁻¹, and tan⁻¹ functions to find angles corresponding to specific trigonometric values. Practice solving equations and converting angles to degrees
0 views • 4 slides
Inverse Condemnation: Legal Aspects and Case Studies
Explore the concepts of inverse condemnation, Serbonian Bog references, and the legal implications in Texas jurisprudence. Learn about typical and atypical claims, challenges faced by plaintiffs and defendants, and notable cases such as Harris Cty. Flood Control Dist. v. Kerr. Delve into government
0 views • 21 slides
Directed Graphs and Adjacency Matrices in Discrete Structures
Explore the concepts of binary relations, directed graphs, adjacency matrices, transitive closure, and walks in the context of discrete structures. Learn how vertices, edges, in-degrees, out-degrees, and self-loops are defined in directed graphs. Understand the importance of adjacency matrices in re
1 views • 28 slides
Reservoir Modeling Using Gaussian Mixture Models
In the field of reservoir modeling, Gaussian mixture models offer a powerful approach to estimating rock properties such as porosity, sand/clay content, and saturations using seismic data. This analytical solution of the Bayesian linear inverse problem provides insights into modeling reservoir prope
0 views • 10 slides
Gravity and Inverse Square Relationships in Physics
Explore the concepts of gravitational field, potential, geostationary orbits, escape velocity, and the inverse square relationship in Newton's Law of Universal Gravitation. Discover how mass and distance affect gravitational force and learn about nonuniform gravitational fields and equipotential lin
0 views • 22 slides