Understanding Bernoulli's Equation in Fluid Mechanics
Bernoulli's equation, a fundamental principle in fluid dynamics, relates pressure, kinetic energy, and potential energy of a fluid flowing in a pipe. Through examples and explanations, explore how this equation can be used to calculate velocity, pressure differences, and forces in various scenarios
1 views • 12 slides
Thermodynamics of Solar Plasma: SAHA-S Equation of State and Recent Results
SAHA-S equation of state (EOS) presents the current state and recent results in thermodynamics of solar plasma. Key authors V.K. Gryaznov, A.N. Starostin, and others have contributed to this field over 20 years. The equilibrium composition between 145 species, including elements and all ions, is exp
1 views • 23 slides
Overview of Fluid Mechanics: Branches, Flow Types, and Equations
Fluid mechanics is subdivided into three branches: Fluid Static, Kinematics, and Hydrodynamics. The study of fluid flow includes different types such as uniform, non-uniform, steady, and unsteady flow. The motion of fluid particles obeys Newton's laws, and the conservation of mass and energy plays a
1 views • 4 slides
Understanding Fluid Mechanics: Archimedes, Pascal, and Bernoulli
Explore the principles of fluid mechanics including Archimedes' Principle, Pascal's Law, and Bernoulli's Principle. Learn about mass density, buoyant force, and the behavior of floating objects in liquids. Discover how the buoyant force is equal to the weight of displaced fluids, and how it affects
0 views • 22 slides
Understanding the Quantity Theory of Money: Fisher vs. Cambridge Perspectives
The Quantity Theory of Money explains the relationship between money supply and the general price level in an economy. Fisher's Equation of Exchange and the Cambridge Equation offer different perspectives on this theory, focusing on money supply vs. demand for money, different definitions of money,
0 views • 7 slides
Understanding Fluid Machines: Specific Work and Energy Transfer
In Chapter 3 of "Specific Work of Fluid Machines" by Eng. Mesfin B., the focus is on energy transfer and determination of specific work. The chapter covers topics such as energy loss, total pressure, the Bernoulli equation, and more. Learn how to calculate mechanical energy and power transferred by
4 views • 33 slides
Understanding Structural Equation Modeling (SEM) and Quality of Life Analysis
Structural Equation Modeling (SEM) is a statistical technique used to analyze relationships between variables, including quality of life factors such as physical health and mental well-being. Quality of life is a multidimensional concept encompassing various aspects like social relationships, living
0 views • 21 slides
Fluid Mechanics Problem Solving with Bernoulli and Momentum Equations
Explore solved problems related to Bernoulli and momentum equations in fluid mechanics, including calculations of discharge, velocity, flow types, pressure losses, and energy lines. Dive into scenarios involving conduit profiles, pipeline configurations, and Reynolds number calculations for water an
0 views • 21 slides
Understanding Freezing Time and Freezers for Food Products
Importance of freezing time in the design of freezers is crucial for maintaining food quality during storage. Plank's equation is used to calculate freezing time based on various parameters. Limitations and assumptions of the equation need to be considered for accurate results.
0 views • 15 slides
Understanding Waveguiding Systems and Helmholtz Equation in Microwave Engineering
Waveguiding systems are essential in confining and channeling electromagnetic energy, with examples including rectangular and circular waveguides. The general notation for waveguiding systems involves wave propagation and transverse components. The Helmholtz Equation is a key concept in analyzing el
2 views • 50 slides
Understanding Thermodynamics and Fluid Mechanics Fundamentals for Efficiency
Explore key concepts in thermodynamics and fluid mechanics such as the equation of continuity, the first law of thermodynamics, the momentum equation, Euler's equation, and more. Learn about efficiency, internal energy, and the laws governing energy transfer in various systems. Delve into topics lik
2 views • 12 slides
Flow Measurement Using V-Notch and Weirs in Engineering
Flow measurement in engineering involves the use of V-notch and weirs, such as rectangular weirs and triangular weirs, to calculate discharge rates and velocity of liquids. A V-notch is a triangular obstruction used for flow measurement, while weirs are larger scale structures for measuring river or
1 views • 7 slides
Rearranging Work Equation and Examples
Learn how to mathematically rearrange the work equation and calculate work using the formula W = F x d. Understand the relationship between force, distance, and work through detailed examples and step-by-step solutions.
0 views • 10 slides
Understanding the Hammett Equation in Chemical Reactions
The Hammett equation explores how substituents influence the dissociation of benzoic acid, affecting its acidity. By quantifying this influence through a linear free energy relationship, the equation helps predict the impact of substituents on different processes. Through parameter definitions and m
0 views • 9 slides
Introduction to Dynamic Structural Equation Modeling for Intensive Longitudinal Data
Dynamic Structural Equation Modeling (DSEM) is a powerful analytical tool used to analyze intensive longitudinal data, combining multilevel modeling, time series modeling, structural equation modeling, and time-varying effects modeling. By modeling correlations and changes over time at both individu
0 views • 22 slides
Understanding Separation Columns in Chemical Engineering
Explore the world of separation columns including distillation, absorption, and extraction, along with empirical correlations, minimum number of stages, Fenske equation, Underwood equation, Kirkbride equation, examples, and solutions presented by Dr. Kh. Nasrifar from the Department of Chemical and
5 views • 15 slides
Comprehensive Overview of Freezing Time Methods in Dairy Engineering
Neumann, Tao, and Non-Dimensional methods are key approaches for determining freezing times in unsteady state heat transfer processes in dairy engineering. The Neumann Problem, Tao Solutions, and Cleland and Earle Non-Dimensional Equation offer distinct equations and models to calculate freezing tim
1 views • 8 slides
Understanding Fluid Mechanics in Dairy Engineering: Applications and Numericals
Explore the application of Bernoulli's theorem in pipe flow, friction losses, and discharge calculations in the context of dairy engineering. Learn about pipe discharging from reservoirs, connecting two reservoirs, and pipes in series through detailed explanations and numerical examples.
0 views • 8 slides
Introduction to Quantum Mechanics: Energy Levels and Schrödinger Equation
Quantum mechanics reveals that all systems possess discrete energy levels, determined by solving the Schrödinger equation where the Hamiltonian operator represents total energy. In a particle-in-a-box scenario, potential energy is infinite outside the box. The Schrödinger equation simplifies to a
0 views • 12 slides
Fundamentals of Fluid Flow: Steady, Unsteady, Compressible, Incompressible, Viscous, Nonviscous
Fluid flow characteristics such as steady vs. unsteady, compressible vs. incompressible, and viscous vs. nonviscous play crucial roles in understanding how fluids behave in various scenarios. Steady flow entails constant velocities over time, while unsteady flow involves changing velocities. Liquids
0 views • 11 slides
Understanding Fluid Dynamics: Equations and Applications
Explore the fascinating world of fluid dynamics through concepts like fluid statics, the equation of continuity, Bernoulli's equation, and their practical applications in areas such as household plumbing, aerodynamics, and sports like curveball pitching. Dive into the principles governing the behavi
0 views • 12 slides
Understanding Fluids, States of Matter, and Phase Changes
Exploring key concepts in physics including Bernoulli's Principle, viscosity, cohesion, states of matter (solid, liquid, gas, plasma), phase changes (evaporation, condensation, etc.), density, pressure, and more. Discover the properties and behaviors of fluids in relation to gases and liquids, along
1 views • 54 slides
Fundamental Comparison: Wheeler-DeWitt vs. Schrödinger Equation
The debate on whether the Wheeler-DeWitt equation is more fundamental than the Schrödinger equation in quantum gravity remains inconclusive. While the Wheeler-DeWitt equation presents an elegant formulation, the Schrödinger equation is essential in specific cases. The issue of time and coordinate
0 views • 6 slides
Understanding Fluid Dynamics and Bernoulli's Principle in Real-world Applications
Explore the fascinating world of fluid dynamics with a focus on Bernoulli's principle through real-life examples like air flow in wind tunnels, airplane wings, and even tornado behavior. Discover how changes in fluid velocity affect pressure and how streamlines provide insights into fluid flow behav
1 views • 23 slides
Understanding Open Channel Flow and Mannings Equation
This review covers hydraulic devices such as orifices, weirs, sluice gates, siphons, and outlets for detention structures. It focuses on open channel flow, including uniform flow and varied flow, and explains how to use Mannings equation for calculations related to water depth, flow area, and veloci
1 views • 43 slides
Space-Efficient Estimation of Statistics Over Sub-Sampled Streams
This research focuses on efficiently estimating statistics over sub-sampled streams, particularly in the context of IP packet streams for traffic monitoring. Various types of sampling methods are explored, such as Bernoulli sampling, to compute key metrics like frequency moments, number of distinct
0 views • 22 slides
Exploring Membrane Potential Densities and the Fokker-Planck Equation in Neural Networks
Delve into the concepts of membrane potential densities and the Fokker-Planck Equation in neural networks, covering topics such as integrate-and-fire with stochastic spike arrival, continuity equation for membrane potential density, jump and drift flux, and the intriguing Fokker-Planck Equation.
0 views • 29 slides
Principles of Flight: Understanding Lift Creation in Aircraft
Explore the factors influencing lift generation in aircraft flight, including Newton's Third Law, weight and lift dynamics, Bernoulli's Principle, aerofoil effects, and aerodynamic terms. Gain knowledge on airflow, airspeed, angle of attack, air density, and wing characteristics affecting lift produ
0 views • 37 slides
Leapfrog Scheme for Advection Equation
The provided images illustrate the Leapfrog scheme applied to an advection equation, focusing on the center method in time and space. The stability of the method is analyzed with assumptions regarding the behavior of the solution. Through the exploration of Courant numbers and CFL conditions, the st
0 views • 25 slides
Excel Tutorial: Finding Trendline Equation and Calculating Rates of Change
Learn how to find the equation of a trendline in Excel and use it to calculate rates of change. This step-by-step guide includes importing data, adding a trendline, displaying the equation, and interpreting it for analysis. Make the most of Excel's features for data analysis.
0 views • 11 slides
Linearized Boltzmann Equation in Statistical Mechanics
This lecture delves into the linearized Boltzmann equation and its applications in studying transport coefficients. The content covers the systematic approximation of transport coefficients, impact parameters of collisions, and the detailed solution for a dilute gas system. It explores the notation
0 views • 25 slides
Quantum Chemistry Learning Goals and Concepts
This content covers the learning goals and concepts of quantum chemistry leading up to the Schrodinger equation and potential energy wells, excluding the material on the hydrogen atom introduced later. It explores models of the atom, including observations of atomic spectra, the Bohr model, de Brogl
0 views • 22 slides
Analytical Solutions for 2D Heat Equation with Separation of Variables
Consider the steady-state 2D heat equation with constant thermal conductivity. Analyze analytical solutions using separation of variables method for a square plate with defined boundary conditions. Learn how to express the general form of solutions and apply them to the heat equation in Cartesian ge
0 views • 15 slides
Dynamic Function for Basal Area of Trees Derived from Differential Equation
Mathematical methods presented by Braun and Simmons are used to derive a dynamic function for the basal area of individual trees from a production-theoretically motivated autonomous differential equation. The differential equation and general dynamic function are described, highlighting the relation
0 views • 45 slides
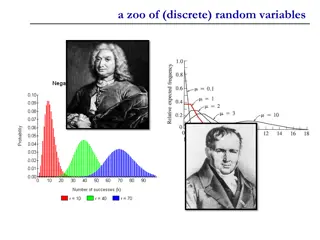
Understanding a Zoo of Discrete Random Variables
Discrete random variables play a crucial role in probability theory and statistics. This content explores three key types: Bernoulli random variable, binomial random variable, and error-correcting codes. From understanding the basics of Bernoulli trials to exploring the application of error correcti
0 views • 27 slides
Understanding Probability with Dr. Zhang at Fordham University
Dive into the world of probability with Dr. Zhang at Fordham University. Explore the basics of experiments, events, and sample spaces, learn how to calculate probabilities using counting methods, rules, and distributions. Understand concepts like conditional probability and the Bernoulli process thr
0 views • 56 slides
Analysis and Comparison of Wave Equation Prediction for Propagating Waves
Initial analysis and comparison of the wave equation and asymptotic prediction of a receiver experiment at depth for one-way propagating waves. The study examines the amplitude and information derived from a wave equation migration algorithm and its asymptotic form. The focus is on the prediction of
0 views • 23 slides
Machine Learning Density Estimation and Bayesian Inference
Delve into the world of machine learning density estimation, parameter estimation, and Bayesian Bernoulli inference. Explore topics such as parametric distributions, binary variables, beta distribution, and more through slides from Professor Adriana Kovashka's lecture at the University of Pittsburgh
0 views • 25 slides
Understanding the Photoelectric Effect and Einstein's Equation
The photoelectric effect is explained by Einstein through assumptions of photons and their interaction with electrons on a metal surface. The maximum kinetic energy of ejected electrons depends on the frequency of incident radiation, as shown in Einstein's Equation. The greater the frequency, the hi
0 views • 6 slides
Graphical Solution of Equations Using GDC - Step-by-Step Guide
Learn how to solve equations graphically using a Graphic Display Calculator (GDC) with step-by-step instructions. Turn on the GDC, input the equation on Y1 and Y2, draw the graphs, and find the intersection point to determine the x-value. An example equation, 2x + 8 = x + 1, is solved using this met
0 views • 20 slides