Understanding Heat Engines and Engine Efficiency
Exploring the concept of heat engines and maximizing efficiency, specifically examining why internal combustion engines have limitations. The discussion covers reversible heat transfer, engine work, efficiency calculations, and practical application to car engines. Insights on temperature differentials and system insulation are highlighted, emphasizing the crucial role of heat transfer in engine performance.
- Heat Engines
- Engine Efficiency
- Internal Combustion
- Temperature Differentials
- Reversible Heat Transfer
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
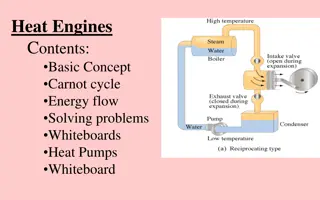
Heat engines and maximum efficiency-or: Why the Internal Combustion Engine Sucks (pp. 837-9 & Fig. 20.7) Qrev,hot Thot http://i.ytimg.com/vi/-0icbqvmehs/0.jpg W https://encrypted-tbn3.gstatic.com/images?q=tbn:ANd9GcRjhsCYWaPBGtiRW4Su97tepPBeCd-H9kpU5emHwLjqASdaYn98QA Heat engine Qrev,cold Tcold To make matters simple-assume the engine and two blocks form a system that is adiabatically insulated from the outside so that no net heat loss to the outside occurs (key notion in `Carnot cycle)
Since we also assume reversible heat transfer, and no heat comes from outside surroundings... Shot + Scold=0 Qrev,hot + Qrev,cold=0 Thot Tcold Note that: Qrev,hot > 0 (engine absorbs heat from hot reservoir ) Qrev,cold < 0 (engine expels heat to cold reservoir) The work* done to move the `bus , W, is derived from the heat sum below, which is really a difference in heats: W= Qrev,hot + Qrev,cold W is a positive heat using the bus s point of view. McQuarrie takes the heat engine s view and is stuck with `hand waving a W = Qrev,hot + Qrev,cold on p. 839
(`eta) = Engine efficiency = W Qrev,hot + Qrev,cold Qrev,hot =1+ Qrev,cold Qrev,hot = Qrev,hot Recall that: Qrev,hot + Qrev,cold=0=> Thot Tcold Qrev,cold = -Tcold Qrev,hot Thot = Thot-Tcold Thot =1- Tcold See also, eq. 20.35 p. 839 Thot
A practical application: car as heat engine The normal engine operating temperature on most new GM cars is ~200oF *. http://www.cargurus.com/Cars/Discussion- t30083_ds38018 * 200 F~ 366 K=Th Assuming room temperature =298 K=Tc = 366-298 366 ~0.19 (19% efficient) = Thot-Tcold Thot