Understanding Pseudo-Noise Sequences and Applications
Pseudo-Noise (PN) sequences are deterministic yet appear random, with applications in various fields such as communication security, control engineering, and system identification. Generated using shift registers, they exhibit statistical properties akin to noise. Linear and nonlinear feedback shift registers classify PN sequences based on the Boolean function used. Statistical properties like period, complexity, randomness, and autocorrelation are crucial in assessing the quality of PN sequences. Choosing taps in maximal-length linear FBSR involves characteristic polynomials to determine sequence quality.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
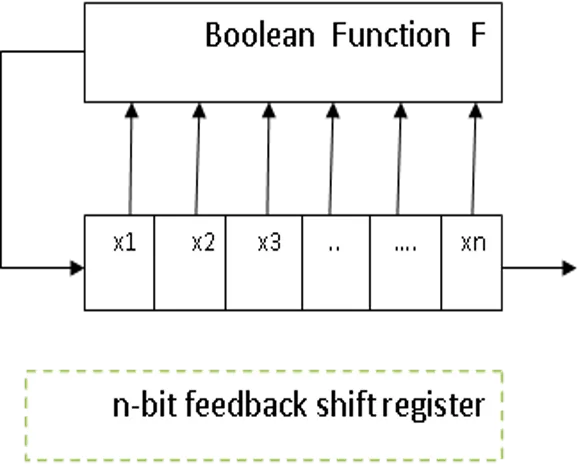
PN Sequences Pseudo-Noise (PN) sequence is a pseudorandom sequence of 1 s and 0 s with some statistical properties that are similar to noise. The sequence looks random from 3rdparty point of view, but it is fully deterministic from the designer point of view. Applications of PN include not only Comsec & Transec but extend control eng.( used in system identification). Generation: There are many practical implementations for PN sequence generator, the simplest is what is called feedback shift register (FBSR). The content PN of the shift register is shifted to the right for each sequence clock pulse and a new serial in bit is generated by a Boolean function.
Depending on this function, Shift register sequences are Classified into linear and nonlinear FBSR. Linear FBSR: In this case, the Boolean function is the Ex-OR only of some selected taps of the shift register: F(x1,x2,x3, ..xn)=a1x1+a2x2+x3a3+ ..+anxn Where the +is the mod-2 addition and aiis a binary variable that specifies the taps to be selected. It should be noted, however, that the key K here is the initial content of the register and the feedback taps (a1, a2,a3, an). The PN sequence output can be taken from the final stage or any previous stage since the only difference is a time shift. Also, parallel outputs can also be used for other applications. This will give a pseudorandom nonbinary sequence. For linear FBSR, the initial content cannot be all zero state since this will lock the register to the zero state. Depending on the taps (a1, a2,a3, an) all statistical properties of the output sequence are determined. Note that there are 2ndifferent ways to choose the taps but not all of these are useful. Before studying the ways to choose the taps, we will study the statistical properties of the output PN sequence:
1-Period P: It is the no of bits after which the shift register repeats itself. For linear type, its maximum is 2n-1 bits. 2-Complexity: It is that part of the PN sequence necessary to find the whole sequence. For linear maximum period PN sequence, only 2n bits are fair enough to find the whole 2n-1 bits. 3-Randomness Properties: These are: a-p(0) & p(1) at the O/P. b-p(00),p(01),p(10),p(11),p(000),p(001),p(010), or the p(run of L bits). For good sequences p(0)=p(1)= 0.5 or in general: p(run of L bits)= (0.5)L. c- Autocorrelation properties: ??? ? = ?=1 ????+? For good sequence, the autocorrelation calculated over one or part of the period(partial correlation) is close to a delta dirac fn., or two-valued with large difference between the inphase and out of phase values, i.e: ?
P Rss(k)= P for k=0,P,2P, . -1 elsewhere k Choosing the taps for P=Pmax=2n-1(maximal length linear FBSR): For any taps (a1, a2,a3, an) , there is a corresponding characteristic polynomial F(x) given by ? ? = 1 + ?=1 ???? (Note that an=1 always otherwise the order of the FBSR willbe less than n) -1 ?
Linear maximal length sequence is obtained if F(x) is irreducible (cannot be factored) and primitive( generates all the elements). The no of such polynomial of degree n is given by: (2? 1) less than L that are relatively prime to L. For example, for n=4, then 15 = 8(intgers less than 15 and relatively prime to 15 are 14,13,11,8,7,4,2,1), hence there are 8/4=2 sets of taps that give Pmaxfor n=4. (note also that ? =L-1 if L is prime). There is no general method that can be used to check or find these polynomials of order n (or taps)satisfying maximal length conditions. A table is given in some books that give these polynomials in terms of the taps to be selected for maximal length as shown below: ? ??? (?)=no of integers ?
N Pmax Taps 3 4 5 6 7 7 15 31 63 127 [1,3] [3,4] [2,5],[2,3,4,5],[1,2,4,5] [1,6],[1,2,5,6],[2,3,5,6] [1,7],[3,7],[1,2,3,7],[2,3,4,7],[2,4,6,7],[1,3,6,7],[2,5,6,7],[1,2,4,5,6,7], [1,2,3,4,5,7] [2,3,4,8],[3,5,6,8],[2,5,6,8],[1,3,5,8],[1,5,6,8],[1,6,7,8],[1,2,5,6,7,8], [1,2,3,4,6,8] [4,9],[3,4,6,9],[4,5,8,9],[1,4,8,9],[2,3,5,9],[5,6,8,9],[2,7,8,9] . 8 255 9 10 511 1023 [3,10],[2,3,8,10],[1,5,8,10] [1,11],[2,5,8,11], . 11 2047 [1,4,6,12],[2,3,9,12], 12 4095 In above table, only half of the true taps are given. The 2ndhalf can be obtained by subtracting other than antaps from n to obtain the new taps. For example, for n=4, table above gives only [3,4], the 2ndset is [4-3,4]=[1,4] and so on. It should be noted, however, that the two PN sequences obtained from the [4,3] or [4,1] taps are the same except for a time shift between them.
Example: Generate the linear maximal length PN sequence obtained from the taps[1,4]. Then find its properties. Q1 Q2 Q3 Q4 Here F(x)=1+x+x4and: 1 1 1 1 Starting with any 4-bit state ( except zero state), following the sequential generation of each bit in the register, then we notice that the register will repeat itself after 15 clock pulses. Hence, yes, the period is 24-1=15, and the output sequence is: 0 1 1 1 1 0 1 1 0 1 0 1 1 0 1 0 Q1 Q2 Q3 Q4 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 1 S(i)=11110101100100011110 0 1 0 0 Full period 0 0 1 0 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0
To test other properties, then: a-p(0)=7/15, p(1)=8/15 0.5. b-p(00)=3/15, p(01)=4/15, p(10)=4/15, p(11)=4/15 0.25 almost equal, and so on for run of 3 bits c-Autocorrelation: To find Rss(k) for k=0 to P-1, then cyclically shift S(i) to the right by k and find the no of bits that agrees and no of bits that disagrees, then: Rss(k)=(no of bits that agrees)-(no of bits that disagrees) For k=0, then: 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0 Agree bits=15, disagree bits=0, Rss(0)=15-0=15 For k=1, then: 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0 0 1 1 1 1 0 1 0 1 1 0 0 1 0 0 Agree bits=7, disagree bits=8, Rss(1)=7-8=-1 For k=2, then: 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0 0 0 1 1 1 1 0 1 0 1 1 0 0 1 0 Agree bits=7, disagree bits=8, Rss(2)=7-8=-1, and so on Rss(3)=Rss(4)= .Rss(14)=-1
Rss(k) Rss(k)= 15 for k=0 15 -1 for k=1,2,3, A parameter of the Rss(k) is called index k of discrimination ID, where: ID=Rss(0)-(max(Rss(k), k 0), here -1 ID=15-(-1)=16. (Note: High index of discrimination is not so much important in Comsec, but it has a great importance in Transec as will be shown later.) Also, the normalized Rss(k) is obtained by dividing by P=15 Rss(k)= 1 for k=0 -1/15 for k=1,2,3,
Homework1: For previous example, find Rss(k) if: a-partial period (say half of the period) is used in correlation(partial correlation). b- one error occurred and correlation is carried out over full period. Homework2: Repeat previous example for non-maximal length sequence obtained using the taps [4,5]. Linear FBSR as a state machine Let v(i) be a column vector representing the state of the shift register at time i, then: v(i+1)=[A] v(i) mod-2, where [A] is a binary nxn transition matrix representing the taps. The [A] matrix is always of the form with taps written in the 1strow, 1's just below the main diagonal and 0's elsewhere. For example, if the taps are [1,4], then:
1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 ? = Suppose that the cryptanalyst knows 2n successive bits of the sequence, then he can write: G(1)=[v(1) v(2) v(3) ..v(n)] and, G(2)=[v(2) v(3) v(4) .v(n+1)] Where G(1) & G(2) are nxn matrices, each column in them is the successive states of the shift register. Then G(2)=[A] G(1) and [A]=G(2) [G(1)]-1,i.e. [A] can be found from 2n successive bits. If [A] is known then the key is known. Hence, the complexity of linear FBSR is 2n bits( this is a weak point). The 3rdparty can know the whole 2n-1 if he knew only 2n bits.
Example: Apply the above procedure for the 4thorder LFBSR with taps [1,4]. Solution: Recall the sequence 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0. Take the, say last 8 successive bits 1 1 0 0 1 0 0 0 , then: v(1)=[0011], v(2)=[1001], v(3)=[0100], v(4)=[0010] and v(5)=[0001] and: 0 1 0 0 0 0 1 0 1 0 0 1 1 1 0 0 As a homework, check that [G(2)] [G(1)]-1 =[A]. Recurrence Relation of the Linear FBSR: Let the output PN sequence be s(i) for i=0 to P-1, then if the 1stn bit is known (initial state), then the next bits can be found in terms of the taps(a1, a2, ..an) and the present state, i.e., 1 0 0 1 0 1 0 0 0 0 1 0 0 0 0 1 [G(1)] = and [G(2)] =
? ? ? = ??? ? ? ??? 2 ?=1 This is called the recurrence relation. For example, if the taps are [1001], and the initial state is [1111]=[S(1),S(2),S(3),S(4)], then: ? ? 5 = ??? 5 ? ??? 2 ?=1 S(5)=a1S(4)+a2S(3)+a3S(2)+a4S(1)=1+0+0+1=0 and S(6)=a1S(5)+a2S(4)+a3S(3)+a4S(2)=0+0+0+1=1 and S(7)=a1S(6)+a2S(5)+a3S(4)+a4S(3)=1+0+0+1=0 and S(8)=a1S(7)+a2S(6)+a3S(5)+a4S(4)=0+0+0+1=1 and so on Note: This recurrence relation is useful to find the taps if 2n successive bits are known to the cryptanalyst. The problem is reduced into solving a set of n simultaneous linear equations over mod2(GF(2)).
Nonlinear Feedback Shift Register: In linear FBSR, the feedback function is mod2 addition of some selected taps. However, nonlinear sequences is obtained if the feedback fn, contains not only mod2 addition but other nonlinear logic. The general form of combinational logic can be written in a form called Reed-Muller form as: f(x1,x2,x3, xn)=a0+a1x1+a2x2+a3x3+ .+anxn+an+1x1x2+an+2x1x3+ ..+a2n- 1x1xn+a2nx2x3+a2n+1x2x4+ ..+a3n-2x2xn+ ..+a2n-1x1x2..xn where the a s are binary variables. Here, we have 2ntaps, hence we will have 22?different feedback functions. Out of these, there are 2nlinear fns. For n=4, then there are 216=65536 fns of the form: f(x1,x2,x3,x4)=a0+a1x1+a2x2+a3x3+a4x4+a5x1x2+a6x1x3+a7x1x4+a8x2x3+ a9x2x4+a10x3x4+a11x1x2x3+a12x1x2x4+a13x1x3x4+a14x2x3x4+a15x1x2x3x4 So depending on the taps (a0,a1,a2, .a15) all statistical properties (period, complexity, prob and autocorrelation) are determined. However, there is no general complete theory that gives the way to choose these taps for good properties. Sometimes, the period itself cannot be found since it depends also on the initial conditions. As a conclusion, this subject is not very well understood (at least in open literatures) and need more studies. Note: For nonlinear FBSR, if 2n-1 is a prime number (n=2,3,5,7,13,17,19,31,61,89,107,127,.. give 2n-1 as prime), then the period of the nonlinear sequence will be either 1 or 2n-1. Such primes are called Mersenne primes).
Other Nonlinear Arrangements: Although nonlinear FBSR is not very well understood, but the nonlinear behavior of PN sequences is so important for higher security (recall the weak and low complexity of linear PN sequence). This is why many other arrangements were suggested to give better approach to nonlinearity, some of these are: a-Combination of linear MLFBSR into nonlinear Logic: As shown n-MLFBSR are used and their outputs S1 S1, S2, ..Snare applied to a nonlinear Boolean function. In such a case, the nonlinearity is outside the feedback and the properties of the O/P sequence S2 will be: 1-Period: P=LCM (P1,P2, Pn) where LCM is the Least Common Multiple. If P1,P2, Pn are relatively prime, then: P= ?=1 ??=P1P2 Pn MLFBSR period P1 Non Linear Boolean Function MLFBSR period P2 ? Sn MLFBSR period Pn
2-Complexity: This depends on the choice of the nonlinear Boolean function. It was shown that higher complexity can be obtained if long product terms exist in this function. However, this will produce unbalance in the number of 1's & 0's in the truth table of the nonlinear function resulting in moderate statistical properties of the output sequence. A good compromise can be obtained by computer simulation. 3-Randomness Properties: This depends on the choice of the nonlinear fn. Sequences with good statistical properties are obtained if the truth table of the fn has a good balance between 0's & 1's. Note: A well-known sequences were suggested and belong to this type, such as Gold codes, JPL codes, Geffe codes and so on. Homework: Prepare simple notes or lecture on Gold codes.
B- Feedforward Connection: In such a case, one n-stage MLFBSR is used to generate a linear sequence. This sequence is not used, but, in stead, a selected parallel outputs are applied to a nonlinear function to produce a nonlinear sequence. As before, the complexity and randomness linear seq MLFBSR period P1 properties depend on this nonlinear fn. Of course, the period of the nonlinear sequence is the same as linear sequence (2n-1). Nonlinear Boolean fn Synchronization Problem of PN Sequences: nonlinear seq In order to achieve perfect enciphering, deciphering by a PN code, then PN generators at the Tx and the Rx must be in synchronism, i.e both shift registers move in synchronous states. To obtain this, then either:
A-Both register may start at the same instant of time with time error of ?. Then a high stable clock generator is used to maintain synchronization. ( These are TCXO Temperature Compensated crystal Oscillator with stability factor of about 10-6=1ppm-part per million, oven type oscillator with stability factor of 10-8=0.01ppm, or using nuclear type Sesium/Rebidum with stability factor of 10-12). B-Global timing between communication stations by means of satellites that continuously transmit information about the time. Example is the use of GPS (Global Positioning System) with timing accuracy of about 100ns in its civilian type. C-We can use the same idea used in cipher feedback mode of DES. This arrangement is called self synchronized stream cipher as shown below:
P K K function P n-bit FBSR C C Above arrangement will ensure similar states of the two shift registers after at most n bits from switching ON. The two disadvantages of this arrangement are: 1- increased bit error rate by a factor of n and. 2- The statistical properties of the output sequence will depend not only on the feedback function but also on the statistical properties of the plaintext P.