Understanding Circular Motion: Co-Terminal Angles and Radian Measure
Explore the concept of co-terminal angles in circular motion, finding lengths of circular arcs, understanding linear and angular speed, and calculating radian measures. Dive into examples of finding co-terminal angles, determining arc lengths, and converting angles to radians. Discover the relationship between central angles, arc lengths, and radius in circular shapes, with practical applications such as calculating linear speed on circular records.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Concept Questions Section 4.1
Checking in Do you all have any questions?
In-Class Find co-terminal angles. Find the length of a circular arc. Use linear and angular speed to describe motion on a circular path.
Two angles with the same initial and terminal sides but possibly different rotations are called co-terminal angles.
Assume the following angles are in standard position. Find a positive angle less than 360 that is co-terminal with each of the following: a. 400 angle 400 360 = 40 b. 135 angle 135 + 360 = 225
Assume the following angles are in standard position. Find a positive angle less than 2 pi that is co-terminal with each of the following: 13 13 10 3 = = 2 13 5 5 5 5 a. angle 5 30 15 29 15 + = + = 2 15 15 b. angle 15
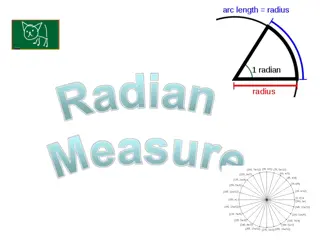
A central angle, in a circle of radius 12 feet intercepts an arc of length 42 feet. What is the radian measure of ? ?= 42 ?? 12 ?? = 3.5 radians ? =
A circle has a radius of 6 inches. Find the length of the arc intercepted by a central angle of 45 . Express arc length in terms of Then round your answer to two decimal places. We first convert 45 to radians: radians 45 45 180 = 4 . 45 180 = = = radians 4 6 = 4.71 inches. inches (6 inches) 4
Long before iPods that hold thousands of songs and play them with superb audio quality, individual songs were delivered on 75-rpm and 45-rpm circular records. A 45-rpm record has an angular speed of 45 revolutions per minute. Find the linear speed, in inches per minute, at the point where the needle is 1.5 inches from the record s center. Before applying the formula we must express in terms of radians per second: = r 90 radians 1 minute 45 revolutions 2 radians 1 minute = = 1 revolution