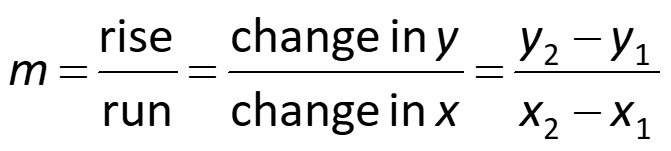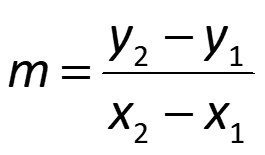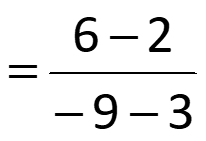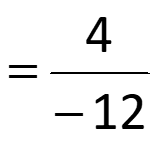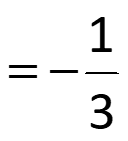Understanding Linear Equations and Graphs
Exploring linear equations in slope-intercept form, the concept of slope, graphing techniques, and real-world applications. Learn about positive and negative slopes, horizontal and vertical lines, slope-intercept form, and interpreting graphs. Examples guide you through finding slope, graphing lines, calculating y-intercepts, and understanding linear functions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Sec 3.5 Graphing Linear Equations in Slope-Intercept Form
Slope of a Line Slope of a line A number that describes the steepness of a line The constant rate of change between points of a linear function m is used to represent slope y y rise change in y = = = 2 1 Formula for Slope of a Line: m run change in x x x 2 1 Ex #1: Find the slope of the line going through points (3, 2) and ( 9, 6) y y m 9 4 6 2 = = 2 1 3 x x 2 1 1 = = 12 3
A line going up from left to right has a positive slope A line going down from left to right has a negative slope A horizontal line has a slope of 0 A vertical line has an undefined slope
Ex #2 Graph a line that has a slope of 2 and goes through the point ( 4, 5) rise = = 2 = m 2 1 run down 2, right 1
Slope-Intercept Form mx y = + b slope y-intercept Ex #3: Graph the equation y = x 4 using the slope and y-intercept m= b = 4 up 2, right 5 (0, 4)
Ex #4: Graph the equation 2y + 8 = 6x + 10 using the slope and y-intercept 2y + 8 = 6x + 10 8 8 2y = 6x + 2 2 = y 2 3 + x 2 1 = = 3 m 3 down 3, right 1 (0, 1) 1 = b 1
Ex #5 A linear function g model a relationship in which the dependent variable increases 3 units for every 1 unit the independent variable increases. Graph g when g(0) = 6. Find the slope, the y-intercept and write the equation of the function. Since g(0) = 6, the line goes through the point (0, 6). So, b = 6 rise 3 = = = 3 m run y 1 = + mx b = x g ( x ) 3 6
Ex #6 A submersible that is exploring the ocean floor begins to ascend to the surface. The elevation h (in feet) of the submersible is modeled by the function h(t) = 650t 13,000, where t is the time (in minutes) since the submersible began to ascend. a) Graph the function and identify the domain and range b) Interpret the slope and the intercepts of the graph Graph using intercepts: h- intercept is 13,000 0 = 650t 13,000 13,000 = 650t 20 = t t- intercept is 20 D:0 t 20 R: 13,000 h 0 4 12 0 8 16 20 20 ( t ) 0 , , 4 000 , 8 000 12 000 , , 0 ( 13 000 , ) The submersible began at a depth of 13,000 ft. below sea level and took 20 minutes to surface. h